Factors Affecting Peace Levels in Afghanistan
Joseph Michael Stockermans[1], Department of Economics, International Christian University, Tokyo, Japan
Abstract
This article develops a microeconomic model of the decision-making process between the two actors involved in the ongoing coalition conflict in Afghanistan, NATO and the insurgents. A unique data set is utilised in order to test whether increases in the applied level of military force result in higher levels of peace for the country. This article finds no evidence to support the idea that exogenous increases in the number of deployed troops increase peace in Afghanistan.
Keywords: Afghanistan, war, peace, 2SLS, econometric, NATO, ISAF, insurgents, coalition
Introduction
The purpose of this article is to measure the extent to which increases in the level of applied NATO military force increase peace and security in Afghanistan. This article models the basic microeconomic decision-making process of the two actors involved in the conflict, NATO and the insurgents. A unique data set is then used to evaluate empirically the NATO-led International Security Assistance Force's (ISAF) achievement of its top objective: to establish peace and security in Afghanistan. This article is unique as attempts to measure the effectiveness of military policy in combating insurgents are not found in the literature, as most economic literature on the war in Afghanistan focuses on the relationship between opium prices and conflict levels (see Bove and Elia, 2011 and Lind et al., 2009). Similarly, microeconomic models of insurgent versus coalition military behaviour are non-existent in the literature.
The Model
Microeconomic Foundations
Two decision-making agents are present in the war in Afghanistan: the NATO-led ISAF and the insurgents. The insurgent objective function is shown in Equation 1, where (P) is the level of peace supplied by the insurgents (low levels of peace indicate fighting), (MF) is the level of military force supplied by the ISAF, and (U) is insurgent utility.
Equation 1 describes how insurgents attempt to maximise their utility by decreasing the level of peace (increasing fighting), in attempt to lower the ISAF military presence in their country. This lowered military presence subsequently increases insurgent utility. The relationships between these variables are shown in Equations 2 and 3 respectively.
Insurgents maximise their objective function subject to the insurgent budget constraint, shown in Equation 4, where mi is insurgent income, pi is the marginal cost faced by the insurgents in decreasing peace by one unit and Pdi is the change in peace demanded by the insurgents.
Preferences are assumed to be non-satiable and the insurgents therefore face a binding budget constraint. Sautter (2010) provides a similar description of terrorist utility maximising behaviour, upon which this article's microeconomic model is loosely based. The ISAF's objective function is shown in Equation 5.
Equation 5 describes how the ISAF attempts to maximise peace by increasing the size of their military presence in the country. The relationship between variables is shown in Equation 6.
The ISAF maximises its objective function subject to the ISAF budget constraint, shown in Equation 7, where mISAF is the ISAF income and pISAF is the marginal cost faced by the ISAF in increasing deployed military force levels by one unit.
While this article assumes the ISAF preferences to be non-satiable, the ISAF's behaviour will not be bound by their budget constraint, as it is assumed that they are further limited by a stronger constraint derived from limited public support for the war. This article assumes that the public will only support the deployment of military force up to a given level, with minor deviances in this level allowed in response to exogenous fluctuations in the peace level. This means that once this maximum level is attained, deployed military force will only be allowed to fluctuate in reaction to exogenous changes in the peace level. Much in the same way as a police force maintains a civil security status quo by increasing in size when crime rates increase, and decreasing in size when they fall, the ISAF nations are assumed to maintain a status quo in the conflict by matching exogenous fluctuations in the level of peace with the appropriate level of applied military force to avoid losses. The status-quo constraint is shown in Equation 8, where (SQ) is a measure of the status quo that is equal to the function (k) that takes the set (z) as an input. The set (z) comprises two variables that are assumed to affect the status quo: instability (i), and public support for the war effort specific to each of the ISAF contributing nations (PS), where z = { i, PS}.
Equation 8 describes scenarios in which deployed military force levels are bound by public support. Once bound, an ISAF nation is forced to maintain a reactionary policy and respond to exogenous fluctuations in the level of peace by increasing the level of military force in times of intense fighting, and relaxing military force levels in times of peace, in order to maintain the status quo equal to k. The relationship between peace and military force is shown in Equation 9.
Fluctuations in the level of instability cause changes in the measure of the status quo according to Equation 10.
The reasoning follows that as instability in Afghanistan increases, the goals of the ISAF increase from maintaining peace and security through armed conflict with the insurgents to include pacifying civilian unrest, increasing the demand for a higher equilibrium level of peace. Similarly, fluctuations in the level of public support for the war cause changes in the measure of the status quo according to Equation 11.
The reasoning follows that increased support by an ISAF country's public voter population will result in a higher demand for peace in Afghanistan. Increases in the public demand for peace allow an ISAF nation to exogenously deploy a higher level of military force, shown in Equation 12.
Thus, increases in instability or public support cause the level of military force to exogenously increase for every given level of peace. Bove and Elia (2011) find evidence suggesting the validity of the status-quo constraint when discussing the increased likelihood of high troop numbers in dangerous areas.
Equilibrium in the Model
The model outlined in this article reverts to equilibrium, shown graphically in Figure 1, in which the positive sloping curve represents the ISAF objective function (Equation 5), and the negatively sloping curve represents the status-quo constraint (Equation 8).
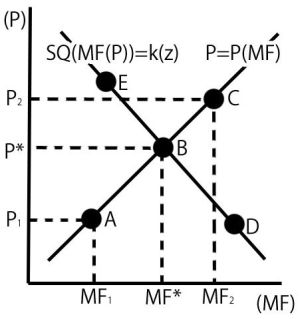
Figure 1: Equilibrium Reversion Process
Reversion to the equilibrium will occur in instances when the level of deployed military force is greater or less than the level supported by the public, or when one side is assumed to overpower the other. To understand this model's equilibrium reversion graphically, assume that an ISAF nation initially deploys a military force level of MF1, resulting in a level of peace equal to P1(point A). As, MF1is below the maximum level of military force supported by the public (MF*), the ISAF nation with non-satiable preferences has not exhausted its public support base and will increase its level of military force until MF=MF*, resulting in a level of peace equal to P* (point B). At this point the ISAF nation has reached the level of military force supported by the public and the status-quo constraint becomes binding. Similarly, examining a situation in which deployed military force is at a level greater than that supported by the public, MF2 (point C), public demand will force the ISAF nation to decrease the deployed level of military force until MF=MF* (point B). Examining a situation in which an ISAF nation is bound by the status-quo constraint and subject to an exogenous decrease in the level of peace, this nation will increase its level of deployed military force until a point such as (D) is achieved. It is assumed that the ISAF nation will increase military force until it overpowers the exogenous decrease in peace. As peace begins to increase, military force levels can be relaxed, and the model converges again to point B. Similarly, given an exogenous increase in the level of peace, an ISAF country may relax its level of deployed military force until a point such as (E) is reached. Insurgents will then take advantage of the vulnerability posed by an ISAF nation's low levels of military force and decrease the level of peace. Military force will then increase to match the increased violence from the insurgents until the publicly supported level at point B is reached. Increases in variables from the set (z) will shift the status-quo constraint rightwards.
The model presented in this article predicts that observable data regarding military force levels and peace levels describe an equilibrium point between an ISAF nation's objective function, and its status-quo constraint. This however, does not allow exogenous changes in the level of military force described by the ISAF objective function to be separable from endogenous changes in the military force level described by the status-quo constraint. Thus, this article makes use of exogenous shifts in the status-quo constraint, to map the equilibrium point at different status quo levels. This allows for the identification of the positive relationship between peace and the level of applied military force described by the ISAF objective function.
Econometric Model
The above framework suggests the following econometric models: Equation 13, which describes a linear version of the ISAF objective function and Equation 14, which describes a linear version of the status-quo constraint.
X is the set of other variables relevant in determining peace levels and military force levels. Equations 13 and 14 impose the exclusion restriction, namely that z only appears in Equation 14, allowing the use of z as an instrument for MF, and hence to consistently estimate b1 in Equation 13.
Data Description
This article uses panel data from 23 of the ISAF countries over a 41-month period starting in September 2006 and ending in January 2010.
Dependent Variable
This article uses the number of troop casualties (defined as troops killed) per country-month observation (denoted as TRPCAS) as a proxy for the dependent variable, peace, with TRPCAS' assumed negative relationship with peace levels shown in Equation 15.
The validity of this proxy is called into question as the ostensible long-term objective of the ISAF has the wellbeing of the country's civilian population in mind, and not the minimisation of troop casualties. However, using short-term data, the use of troop casualties is the most valid measure of the effectiveness of NATO military policy, since the prerequisite of the final goal of reduced suffering of the civilian population is the removal of insurgents from the country. For this reason, this article interprets increasing peace as the removal of insurgents and asserts that TRPCAS is a valid measure of the achievement of the ISAF's short-term goal, as we expect the removal of insurgents to translate into reduced fighting and lower casualties. Civilian casualties, the number of hostages, and other metrics of the suffering of a war-stricken nation's non-military inhabitants would not be a suitable indicator of the effectiveness of military policy as these are seen as the by-products of targeted violence between the ISAF troops and insurgents. This article selects troop casualty counts over troop wounded counts as the proxy for peace because, although data on wounded soldiers consists of fewer zero-valued observations, casualties are a more relevant measure of peace for the families of many soldiers fighting in this conflict. Cordesman (2008) and Cordesman (2012) criticise the use of troop casualties as a metric for peace because of the inability of this metric to take into account peaceful areas under the political and economic control of insurgents, and on the large difference in measurement techniques by different analysing bodies. This article ignores this first problem as areas completely under insurgent control are rare, and overcomes this last issue by using data obtained from the iCasualties website, in line with the methods used by Lind et al. (2009).
Explanatory Variables
The explanatory variables used in this analysis are divided into four groups: military force level indicators, status quo shifting variables, seasonal indicators, and regional indicators. All status-quo shifting variables are included in the set (z) of the econometric model. With the exception of TROOPS, all military force level variables, seasonal variables, and regional variables are included in set (X) of the econometric model.
Military Force Level Indicators
This article uses the number of troops deployed in Afghanistan per country-month observation (denoted as TROOPS) as a proxy for the main explanatory variable, military force. The assumed positive relationship between military force levels and its proxy, number of deployed troops, is shown in Equation 16.
The obvious way to minimise troop casualties, and thus increase this article's proxy for peace, is by deploying zero troops; this suggests a lack of validity of this proxy in combination with TRPCAS. This comes logically since fewer troops deployed in Afghanistan allow for fewer occasions for casualties. However, this article overcomes this limitation for the following reason. Bove and Elia (2011) find evidence that insurgent activities are sticky with respect to funding, indicating that insurgents may spend a lot of time planning attacks. This means that, constrained by their budget and subject to an exogenous surge in troop numbers, it is unlikely in the short term that insurgent activities can increase in intensity sufficiently quickly for this surge to directly translate into increased occasions for casualties. This suggests that any positive correlation between troop casualties and troop numbers observed in the short-run data is likely due to movement along the status-quo constraint; a reactionary military policy.
Data on deployed troop numbers were obtained from the official NATO website. Figure 2 displays deployed troop numbers for the two countries with the highest levels of deployed troops, the US and the UK, and the ISAF average over the period analysed by this article.
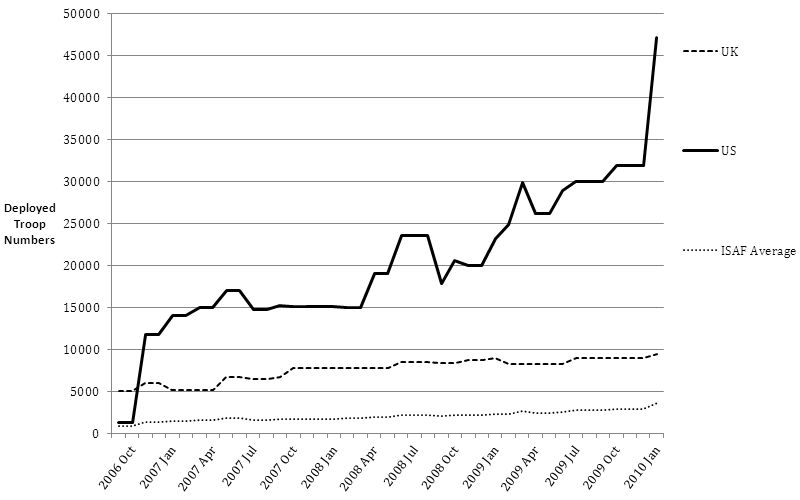
Figure 2: Deployed Troop Levels
Along with the number of deployed troops, annual defence expenditure per country-month observation, denoted as DE, and annual defence expenditure as a per cent of nominal GDP per country-month observation, denoted as DEGDP, are included in the set of military force level indicators. Although these variables are aggregate measures and are not the fraction of defence expenditure used for the war in Afghanistan, they do provide some insight into the size of, and how well equipped and trained each nation's military is. These variables are predicted to have a positive effect on levels of peace in Afghanistan. Defence expenditure data were obtained from the official NATO website and current GDP data from the World Bank website.
Status Quo Shifting Variables
This article uses a set of variables representing measures of instability as instruments to shift the status-quo constraint. The monthly number of civilian casualties in Afghanistan (CIVCAST), the number of reported foreign journalist casualties per country-month observation (JRNFCAS), the number of reported cases of hostility against foreign journalists per country-month observation (JRNFHOSTILITY), and the number of reported cases of hostility against all journalists per month (JRNTHOSTILITY) represent civilian instability. Increases in all of these variables are expected to increase the status-quo constraint to a higher level of equilibrium peace.
The monthly price of Afghanistan opium (OPPRICE), the monthly opium output of Helmand province, Afghanistan's largest opium producing region (OPHELMAND), the total farmland in Afghanistan currently being used to grow opium-producing poppies per month (OPTFRMLND), the annual total value of Afghanistan produced opium (OPOUTVALUE), and the annual total output of Afghanistan produced opium (OPTOUT) are the opium-related instability metrics used in this article. The sign of the correlation between opium-related variables and peace is expected to be ambiguous and depends on whether farmers or insurgents capture the profits (see Bove and Elia, 2011 and Lind et al., 2009). Opium-related data was obtained from the United Nations Office on Drugs and Crime, Afghanistan Opium Survey 2009, journalist data from the Reporters Without Borders website, and civilian casualty data from the British national daily newspaper The Guardian and from the United Nations Assistance Mission in Afghanistan website.
Apart from instability indicators, this article also uses a dummy variable for each ISAF country over the observed 41-month period as a proxy for public support for the war effort, in order to shift exogenously the status quo. The reason for this shift is as follows: the more an ISAF-contributing nation's
voting populace wants to resolve the conflict in Afghanistan the greater the number of troops it will be willing to deploy and the more money it will be willing to expend. This consequently increases the equilibrium level of peace. Because the intensity of fighting in Afghanistan differs greatly by region, and countries with headquarters in regions of intense fighting are most likely to deploy a higher level of troops, regional variation will need to be controlled for before these dummy variables can be considered exogenous. Once regional variation in troop numbers is controlled for, these dummy variables will measure the exogenous, time-invariant effect that country-specific factors have on the number of deployed troops, which may be the result of domestic and foreign pressure, including public voter demand, political pressure from abroad, or humanitarian values. Although support for the war effort is likely to be time-variant, this article employs time-invariant dummy variables due to data limitations. Similarly, although over time within a country, public support is likely to be a decreasing function of troop casualties, and thus the exogeneity of the variables is brought into question, the withdrawal behaviour of countries from the war suggest that troop casualties is not a significant determinant of public support when compared across countries. This is because the first of the ISAF countries to refuse to contribute additional troops and to begin withdrawing troops from Afghanistan have been countries with comparatively small casualty counts.
Seasonal Indicators
The time trend of all 41 months of data (TIME), a dummy variable representing the spring months (SSNSPRING), a dummy variable representing the summer months (SSNSUMMER), a dummy variable representing the autumn months (SSNAUTUMN), and a dummy variable representing the winter months (SSNWINTER) represent the seasonal and temporal variables used as controls in this article's econometric model. As the altitude of Afghanistan ranges from 500 to 8000 metres above sea level, with most of the fighting occurring in the southeast of the country at an average of 4000 meters above sea level (a third of the cruising altitude of a standard easyJet flight aboard an Airbus 319), insurgents may choose not to fight the ISAF troops as much in the frigid temperatures caused by winter. For this reason, the summer season is predicted to have a negative effect on the level of peace and the winter season is predicted to have a positive effect on the level of peace. The effects of the spring and autumn seasons on peace levels are ambiguous and most likely depend on the average temperature during these months.
Regional Indicators
The number of coalition headquarters in the northern region of Afghanistan per country-month observation (REGNORTH), the number of coalition headquarters in the western region of Afghanistan per country-month observation (REGWEST), and the number of coalition headquarters in the region surrounding the capital city of Afghanistan, Kabul, per country-month observation (REGCAPITAL) represent the regional variables used as controls in this article's econometric model. Countries with headquarters in the west, north, and capital will likely have less troop casualties as most of the fighting occurs along the Afghanistan-Pakistan border to the southeast of the country. Regional headquarter data was obtained from the official NATO website. Units on all variables are shown in Table 1.
| Variable | Units | |
|---|---|---|
| Dependent Variable | TRPCAS | Number of deaths |
| Military Policy | TROOPS | Number of people |
| DE | Million US$ | |
| DEGDP | % | |
| Instability Indicators | CIVCAST | Number of people |
| JRNFCAS | Number of people | |
| JRNFHOSTILITY | Number of cases | |
| JRNTHOSTILITY | Number of cases | |
| OPPRICE | US$/Kg | |
| OPTOUT | Metric Tons | |
| OPOUTVALUE | US$/Kg | |
| OPHELMAND | Metric Tons | |
| OPTFRMLND | Hectares | |
| Temporal Indicators | TIME | Integer from 1 to 41 |
| SSNSPRING | if yes =1, if no =0 | |
| SSNSUMMER | if yes =1, if no =0 | |
| SSNAUTUMN | if yes =1, if no =0 | |
| SSNWINTER | if yes =1, if no =0 | |
| Regional Indicators | REGNORTH | Number of HQ |
| REGWEST | Number of HQ | |
| REGCAPITAL | Number of HQ |
Table 1: Units
Empirical Results
The following section will use exogenous changes in fighting caused by temperature fluctuations to test for the existence of a reactionary military policy, indicative of a status-quo constraint. The subsequent section estimates a reduced form equation, tests for the endogeneity of the variable TROOPS, and ultimately estimates a two-stage least squares model in attempt to identify the ISAF objective function.
Evidence for the Status-quo Constraint
One source of evidence for the existence of the status-quo constraint comes from the seasonal variables. Figure 4 depicts the total number of troop casualties over time and shows spikes corresponding to the grey bands, representing the warmer months. This is likely to be a result of how extreme cold deters insurgent activity during the winter months causing an exogenous increase in the level of peace.
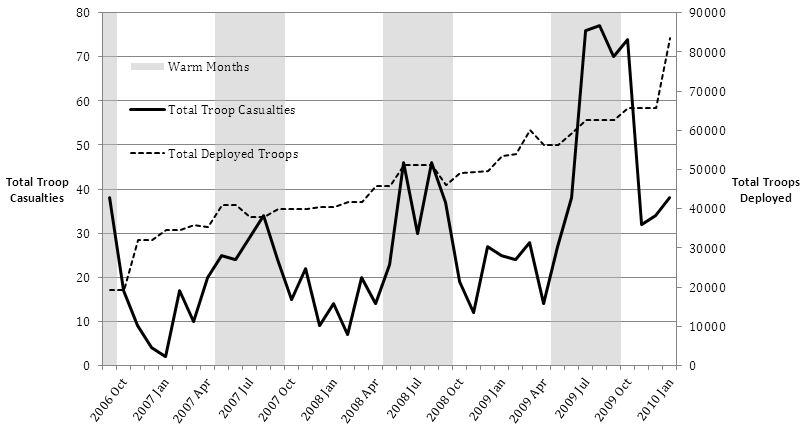
Figure 3: Total Troop Casualties and Total Deployed Troops
The first column of Table 2 shows a fixed effect regression of TROOPS on the seasonal dummy variables.
| Variable | (1) | (2) |
|---|---|---|
| C | 2.196E+3*** (1.283E+2) |
2.006E+3*** (6.727E+1) |
| SSNWINTER | -1.011E+2 (1.730E+2) |
- |
| SSNSPRING | -1.785E+2 (1.815E+2) |
- |
| SSNAUTUMN | -2.803E+2* (1.697E+2) |
- |
| SSNSUMMER | - | 4.788E+01 (1.468E+2) |
| USA*SSNSUMMER | - | 3.270E+3*** (7.041E+2) |
| Observations | 943 | 943 |
| R-squared | 0.8427 | 0.8461 |
| Adjusted R-squared | 0.8384 | 0.8420 |
Table 2: Exogenous Fluctuations in Temperature on Troop Numbers
Notes: The dependent variable is the troop count for each country-month observation (TROOPS).
*** Denotes statistical significance at the 1% level.
** Denotes statistical significance at the 5% level.
* Denotes statistical significance at the 10% level
Although only the autumn season is significant at any reasonable level, the signs of all variables are correct and the high R-squared and adjusted R-squared values indicate that after country-specific effects are removed, the seasonal effect on troop numbers is large. These results suggest that relative to the colder seasons, the exogenous decrease in the peace level supplied by the insurgents in the summertime corresponds to increases in deployed troop numbers in Afghanistan, as the ISAF attempts to match troop numbers to meet this exogenous increase in fighting. The second column of Table 2 shows a fixed effect regression of TROOPS on the summer dummy variable and the summer dummy variable interacted with a dummy variable representing the US, in order to observe whether the nation with the largest number of deployed troops also acts in accordance with the status-quo constraint. The interaction term is significant at the 1% level and exhibits the expected sign, indicating that the US tends to increase troops in the warmer months of the year, matching the exogenous increase in insurgent attacks.
Simultaneous Equations Model
The equilibrium between the ISAF objective function and the status-quo constraint explains how the level of applied military force and the level of peace are jointly determined. The ISAF objective function depicts the level of peace as an increasing function of the level of applied military force, and the status-quo constraint depicts the level of applied military force as a decreasing function of the level of peace. Figure 4 displays a scatter plot of TRPCAS and TROOPS. This graph includes data from all 23 countries over the 41-month period analysed, displaying the positive relationship between these two variables[2], indicative that the data describes the equilibrium point between the ISAF objective function and the status-quo constraint. Thus, this article makes use of exogenous shifts in the status-quo constraint, to allow for the identification of the ISAF objective function. This article uses instability indicators and country-specific dummy variables as instrumental variables for TROOPS to account for shifts in the status-quo constraint, allowing for the accurate estimate of the coefficient b1 from Equation 13.
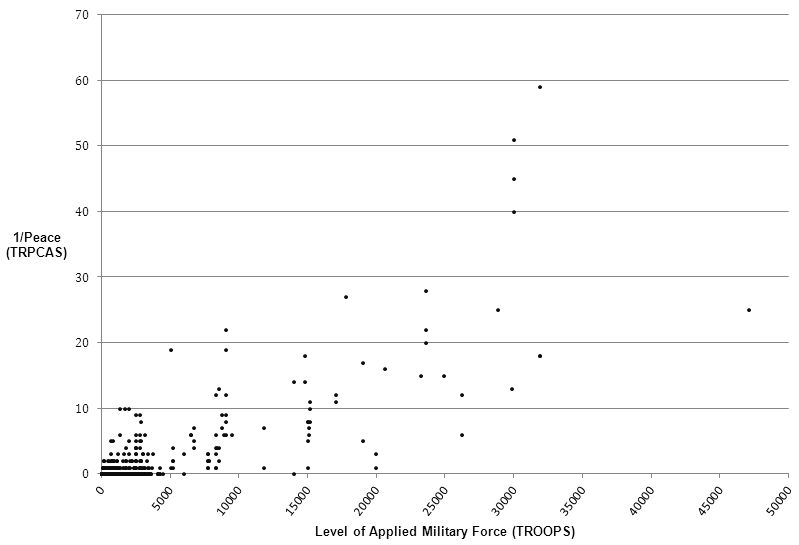
Figure 4: Relationship between TRPCAS and TROOPS
Estimation of the reduced form equation is shown in Table 3.
| Variable | (1) | (2) |
|---|---|---|
| C | 1.186E+4 (4.861E+4) |
7.808E+3 (2.043E+4) |
| JRNFHOSTILITY | 1.951E+3 (1.300E+3) |
5.323E+2 (5.518E+2) |
| JRNFCAS | 1.585E+3 (1.770E+3) |
4.690E+2 (7.478E+2) |
| JRNTHOSTILITY | -1.103E+1 (3.468E+1) |
-0.5786 (1.458E+1) |
| OPHELMAND | -0.0028 (0.0660) |
-0.0101 (0.0277) |
| OPOUTVALUE | 0.0094 (0.0478) |
0.0040 (0.0201) |
| OPPRICE | -8.763E+1 (3.754E+2) |
-4.119E+1 (1.577E+2) |
| OPTFRMLND | -0.0026 (0.0462) |
-0.0061 (0.0194) |
| OPTOUT | -1.0471 (7.8780) |
-0.1422 (3.3104) |
| SSNSUMMER | -1.719E+1 (4.544E+2) |
3.047E+1 (1.910E+2) |
| SSNAUTUMN | -2.365E+1 (4.262E+2) |
1.366E+1 (1.791E+2) |
| REGNORTH | 6.407E+1 (1.759E+2) |
-1.973E+3*** (3.886E+2) |
| REGWEST | 1.808E+3*** (2.476E+2) |
1.646E+4*** (3.876E+2) |
| REGCAPITAL | -5.989E+2* (3.301E+2) |
2.421E+3*** (3.018E+2) |
| Country Specific Dummy Variables Included | no | yes |
| Observations | 943 | 943 |
| Prob(F-statistic) | 0.0026 | 0.0000 |
| R-squared | 0.0779 | 0.8405 |
| Adjusted R-squared | 0.0650 | 0.8349 |
Table 3: Reduced Form
Notes: The dependent variable is the troop count for each country-month observation (TROOPS).
The Prob(F-statistic) is measured with regards to all variables excluding SSNSUMMER, SSNAUTUMN, REGNORTH, REGWEST, and REGCAPITAL.
Results for country-specific dummy variables (not shown) have coefficients ranging from -12711 to -20171, and all are significant at the 1% level.
The first column of Table 3 displays the results of estimating a reduced form equation only on instability indicators. The R-squared and adjusted R-squared values are shown to be low even though the F-statistic for the significance of all instability indicators rejects the null hypothesis at the 1% level. This suggests that while relevant, instability indicators may be weak instruments for troop numbers. The second column of Table 3 includes the country-specific dummy variables for public support in the estimation of the reduced form equation. The F-statistic for the significance of all instruments has increased to a value of 160, and the R-squared and adjusted R-squared terms have also increased considerably, suggesting that after controlling for regional and seasonal affects, exogenous country-specific factors explain much more of the variation in TROOPS than instability indicators do. Table 4 displays the results of a Hausman-Wu test, conducted to confirm the endogeneity of TROOPS.
| Variable | Country Specific Dummy Variables Included | Country Specific Dummy Variables Not Included |
|---|---|---|
| C | -0.4059*** (0.1497) |
-0.6690*** (0.2485) |
| TROOPS | 0.0008*** (2.08E-5) |
0.0009*** (0.0001) |
| SSNSUMMER | 0.9938*** (0.2176) |
0.9728*** (0.2184) |
| SSNAUTUMN | 0.6149*** (0.1980) |
0.6384*** (0.1990) |
| REGNORTH | -0.5200*** (0.1014) |
-0.5448*** (0.1031) |
| REGWEST | -0.2704* (0.1496) |
-0.5556** (0.2620) |
| REGCAPITAL | -0.4050** (0.1928) |
-0.3305 (0.2010) |
| REDUC_RESID | 9.10E-5* (5.07E-5) |
0.0001 (0.0001) |
| Observations | 943 | 943 |
| R-squared | 0.6690 | 0.6683 |
| Adjusted R-squared | 0.6665 | 0.6658 |
Table 4: Hausman-Wu Test for Endogeneity
Notes: The dependent variable is the soldier casualty count for each country-month observation (TRPCAS).
The REDUC_RESID term is the residual from the reduced form equation.
In the first column of Table 4, the residual from the reduced form equation including country-specific dummy variables (column two of Table 3) is shown to be significant at the 10% level, suggesting that TROOPS and TRPCAS are reasonably endogenous. Contrastingly, in the second column, the residual from the reduced form equation excluding country-specific dummy variables (column one of Table 3) is shown to be insignificant at any reasonable level, contradicting the results of the first column. This suggests that instability indicators may not be in fact exogenous, and thus will not be suitable for use as status-quo constraint shifters. For this reason, the inclusion of country-specific dummy variables is necessary to estimate accurately coefficient b1 from Equation 13. Table 5 displays the results of the two-stage least squares estimation of Equation 13 along with an OLS estimation and a Poisson estimation for comparison. A Poisson estimation is used to facilitate analysis because the dependent variable used in this article is a form of count data that contains small non-negative integers biased towards zero because of the many observations with zero values. Exact specifications for the OLS and Poisson estimations are shown in Appendix A.
| Variable | 2SLS | 2SLS with lag | OLS | Poisson |
|---|---|---|---|---|
| C | -0.4059*** (0.1499) |
-0.4743 (0.3088) |
-0.4317*** (0.1492) |
-1.1721*** (0.0795) |
| TROOPS | 0.0008*** (2.08E-5) |
2.193E-3*** (5.40E-4) |
0.0008*** (0.0000) |
0.0001*** (0.0000) |
| TROOPS(-1) | - | -1.499E-3*** (5.71E-4) |
- | - |
| SSNSUMMER | 0.9938*** (0.2180) |
1.0862 (0.7016) |
0.9918*** (0.2179) |
1.0535*** (0.0739) |
| SSNAUTUMN | 0.6149*** (0.1983) |
0.5526 (0.4870) |
0.6172*** (0.1982) |
0.7909*** (0.0756) |
| REGNORTH | -0.5200*** (0.1015) |
-0.4204*** (0.0709) |
-0.5224*** (0.1015) |
-0.4497*** (0.0854) |
| REGWEST | -0.2704* (0.1498) |
-0.2857* (0.1623) |
-0.2984** (0.1489) |
-0.0894 (0.0616) |
| REGCAPITAL | -0.4050** (0.1931) |
-0.7335*** (0.1654) |
-0.3977** (0.1930) |
-0.3602*** (0.0772) |
| Instrumental variables | yes | yes | no | no |
| Other control variables | no | no | yes | yes |
| Observations | 943 | 920 | 943 | 943 |
| R-squared | 0.6676 | 0.5900 | 0.6678 | 0.1939 |
| Adjusted R-squared | 0.6655 | 0.5869 | 0.6657 | 0.1888 |
Table 5: The ISAF Objective Function Estimation Results
Notes: The dependent variable is the soldier casualty count for each country-month observation (TRPCAS). OLS and Poisson regression control for: TROOPS^2, DE, DEGDP, CIVCAST, JRNFCAS, JRNFHOSTILITY, OPPRICE, OPOUTVALUE, OPTFRMLND, and TIME.
Results from the two-stage least squares estimation shows that the summer and autumn months are positively correlated with increased troop casualties. This is likely to be due to a decrease in willingness to fight on the insurgent side as a result of the drop in temperature. The northern, western, and capital city regions are negatively correlated with troop casualties. This result is also expected, as the regions of intense fighting are concentrated along the southeast of the country, near the Pakistan border. The negative valued constant term illustrates the limitations of this article's model, as the negative sign implies that if troop counts were equal to zero, we would observe negative troop casualties. This result does not make logical sense and suggests that this model is only valid at large levels of troop counts. TROOPS, despite estimation using a two-stage least squares method, does not exhibit the predicted negative sign and is shown to maintain a consistent positive correlation with troop casualties across estimation techniques, although the negative sign on the lagged TROOPS term in the second column does suggest that over time these effects are partially mitigated. Applying the results of the two-stage least squares model to American President Barack Obama's December 2009 announcement of an increase in troops by 30,000 in early 2010, the two-stage least squares model estimates that soldier casualties will increase by 24 deaths per month (19 deaths per month if lagged TROOPS is included). The signs of all other variables are also robust across estimation techniques.
The reason that the shifts of the status-quo constraint involved in the two-stage least squares estimation failed to identify any negative correlation between troop casualties and troop numbers can be explained in the following three ways. First, the use of a time-invariant dummy variable to represent public support for the war may not accurately capture temporal changes in public support that may be important in determining troop numbers; a time-variant measure of public support may be a better option for further analysis. Second, the assumption that increased troops do not translate to increased opportunities for casualties may be invalid, indicating that a different proxy for peace may yield different conclusions from the data. Third, the ISAF objective function may in fact be horizontal, or slightly downward sloping if we accept a small bias from increased opportunities for casualties. This would explain why shifts in the status-quo constraint do not translate into the predicted positive relationship between peace and military force levels. A horizontal ISAF objective function would indicate that peace levels are independent of military force levels, and that NATO policy is largely reactionary.
Taken together, these results provide evidence in support of the conclusion that troop surges as a form of military policy may not be effective in removing insurgents from Afghanistan. A horizontal objective function and the possibility of increasing occasions for casualties with increased troop numbers question the legitimacy of these surges.
Conclusion
After construction of a microeconomic model describing the decision-making process of the two actors involved in the conflict, NATO and the insurgents, this article analysed data regarding the factors affecting peace levels in Afghanistan using a simultaneous equations model. Evidence suggested that factors negatively correlated with this article's inverse proxy for peace, troop casualties, include: having headquarters in the north and western regions of Afghanistan. Factors shown to exhibit positive correlations with troop casualties in Afghanistan include the number of troops stationed in Afghanistan, and the summer and autumn months.
With regard to this article's evaluation of the ISAF's achievement of its top objective to establish peace and security in Afghanistan through the removal of insurgents, military force levels were shown to be robust and positively correlated with troop casualties in Afghanistan despite estimation using a two-stage least squares method in which instability indicators and public support for the war effort were used as instruments. This article argues that these results may be explained in two ways: (1) an ineffective military policy in which the ISAF objective function is horizontal, indicating that peace levels are independent of military force levels, and that the primarily goal is to match troop numbers to expected surges of violence from the insurgents; and (2) the ineffectiveness of this article's assumption that increased troop numbers do not automatically translate into increased opportunities for casualties.
Although policy implications from this article suggest that troop surges are an ineffective means of removing insurgents, further research is needed to come to any significant conclusions. Further research should aim at testing a range of proxy variables for peace and domestic support for the war. Proxies for peace should focus on measuring the effectiveness of NATO in removing insurgents, and not on measures of civilian suffering, and the proxy for domestic support for the war should aim to be time-variant.
Acknowledgments
I would like to thank my Professor Tomo Inoue for all of his help and kindness, my research assistant Miu Ide for her hard work, Divya Raghavan for helping me to edit and Tanaya Devi for her great ideas.
List of Figures
Figure 1: Equilibrium Reversion Process
Figure 2: Deployed Troop Levels
Figure 3: Total Troop Casualties and Total Deployed Troops
Figure 4: Relationship between TRPCAS and TROOPS
List of Tables
Table 1: Units
Table 2: Exogenous Fluctuations in Temperature on Troop Numbers
Table 3: Reduced Form
Table 4: Hausman-Wu Test for Endogeneity
Table 5: The ISAF Objective Function Estimation Results
Table 6 (Appendix A): OLS and Poisson Estimation Results
Appendix A
| Variable | OLS | Poisson | |
|---|---|---|---|
| Military Policy | TROOPS | 0.0008*** (-0.0000) |
0.0004*** (2.4339E-5) |
| TROOPS^2 | 3.0800E-9* (1.7700E-9) |
-6.7387E-9*** (4.5177E-10) |
|
| DE | -2.5200E-7 (2.0900E-6) |
1.1115E-6 (8.0690E-7) |
|
| DEGDP | -0.5203* (0.2714) |
-0.6535*** (0.1564) |
|
| Instability Indicators | CIVCAST | -0.0015 (0.0014) |
-0.0006 (0.0004) |
| JRNFCAS | 2.9759*** (1.0305) |
0.6216** (0.2636) |
|
| JRNFHOSTILITY | -1.3547* (0.7579) |
-0.3902* (0.2325) |
|
| OPPRICE | -0.0023 (0.0214) |
0.0300*** (0.0089) |
|
| OPOUTVALUE | 2.1900E-6 (3.0700E-6) |
-1.1953E-6 (1.3314E-6) |
|
| OPTFRMLND | -1.7500E-5 (1.5100E-5) |
4.2190E-6 (6.3396E-6) |
|
| Temporal Indicators | TIME | -0.0077 (0.0333) |
0.0323** (0.0126) |
| SSNAUTUMN | 0.7910*** (0.2551) |
0.4397*** (0.0926) |
|
| SSNSUMMER | 1.2464*** (0.2658) |
0.7393*** (0.0888) |
|
| Regional Indicators and Constant Term | REGNORTH | -0.6457*** (0.1193) |
-0.4706*** (0.0808) |
| REGCAPITAL | -0.3318* (0.2044) |
0.3368*** (0.1147) |
|
| REGWEST | -0.3328** (0.1587) |
-0.6435*** (0.1201) |
|
| Constant | 2.1354 (3.1574) |
-3.8664*** (1.2398) |
|
| Observations | 943 | 943 | |
| R-squared | 0.7599 | 0.7599 | |
| Adjusted R-squared | 0.7557 | 0.7557 |
Table 6: OLS and Poisson Estimation Results
Notes: The dependent variable is the soldier casualty count for each country-month observation (TRPCAS).
Notes
[1] Joseph completed his BA in International Economics in 2011 at the International Christian University in Tokyo Japan, where he was the recipient of the Nakajima Heiwa Scholarship for academic excellence. In 2012, he was first place winner of the Future Leaders Research Competition, held in cooperation with Reinvention: an International Journal of Undergraduate Research. Joseph is now completing a Master's degree in Economics at Cambridge University.
[2] The Pearson correlation coefficient between these two variables is 0.81 and the Spearman rank correlation is 0.52. The higher Pearson correlation indicates that the linear correlation is larger than the rank correlation. This is likely to be due to the large numbers of observations in variables clustered towards the zero area.
References
Bove, V. and E. Leandro (2011), 'Drugs and Violence in Afghanistan: A Panel VAR with Unobserved Common Factor Analysis', unpublished working paper, Network of European Peace Scientists Working Paper Series
Cordesman, A. (2008), 'Analyzing the Afghan-Pakistan War', available at http://csis.org/publication/ afghanistan-pakistan-war, accessed 29 February 2012
Cordesman, A. (2012), 'Afghanistan: The Failed Metrics of Ten Years of War', available at http://csis.org/ publication/afghanistan-failed-metrics-ten-years-war, accessed 29 February 2012
Datablog (2009), 'Afghanistan Civilian Casualties: Year by Year, Month by Month', The Guardian, available at http://www.guardian.co.uk/news/datablog/2009/nov/19/afghanistan-civilian-casualties-statistics-data, accessed 19 December 2009
Government of Afghanistan Ministry of Counter Narcotics (2009), Afghanistan Opium Survey 2009, Vienna: United Nations Office on Drugs and Crime
International Security Assistance Force (2009), NATO Official Website, available at http://www.nato.int/the ISAF/docu/epub/pdf/placemat.html, accessed 12 December 2009
Lind, J., K. Moene, and F. Willumsen (2009), 'Opium for the Masses? Conflict-Induced Narcotics Production in Afghanistan', unpublished working paper, CESifo Working Paper No. 2573
Reporters Without Borders (2009), Official Reporters Without Borders Website, available at http://en.rsf.org/Afghanistan.html, accessed 9 January 2007
Sautter, J. (2010), 'Variance, Violence, and Democracy: A Basic Microeconomic Model of Terrorism', Journal of Strategic Security, 3 (1), 39-50
White, M. (2009), 'Operation Enduring Freedom', iCasualties, available at http://www.icasualties.org/OEF/, accessed 11 December 2009
World Bank Group (2009), Official World Bank Website, available at http://datafinder.worldbank.org/gdp-current, accessed 7 January 2010
United Nations (2009), United Nations Assistance Mission in Afghanistan, available at http://unama.unmissions.org/, accessed 15 December 2007
To cite this paper please use the following details: Stockermans, J. M., 'Factors Affecting Peace Levels in Afghanistan', Reinvention: an International Journal of Undergraduate Research, Volume 5, Issue 2, www.warwick.ac.uk/reinventionjournal/issues/volume5issue2/Stockermans Date accessed [insert date]. If you cite this article or use it in any teaching or other related activities please let us know by e-mailing us at Reinventionjournal at warwick dot ac dot uk.