Christopher P. Roth^[1], Department of Economics, University of Oxford

Abstract

This article considers a dynamic linear specification of Subjective-Well-Being (SWB) using waves 8 to 18 of the British Household Panel Survey (BHPS). Using the Arellano-Bond (1991) dynamic panel-data estimation technique, this article suggests a theoretical framework for understanding determinants of SWB based on insights from evolutionary psychology and biology. Three major empirical findings consistent with the theoretical framework emerge: regional reference points in different domains are found to be statistically significant; SWB is autoregressive and persistent both for a multi-item scale and a single-item scale measure of SWB; there is adaptation to expenditure on food, but not to social status and expenditure on leisure activities. Based on Rayo and Becker (2007) this article builds an economic argument for the evolutionary principles reflected in the data: it uses a mechanism design setup to give an economic rationale for autoregressive and persistent SWB functions.

Keywords: Life satisfaction, Dynamic models, Adaptation, Reference-Dependence, Evolutionary Psychology, Panel Data

 

Introduction

Interest in SWB measures results from the increasing doubts among many economists 'as to whether utility can generally be derived from observable choices' (Powdthavee, 2007: 8) as posited by the objectivist revealed preferences approach (RPA). A new emphasis on bounded rationality (Simon, 1972) and heuristic-based decision-making has accentuated the complementary role SWB measures should play in assessing an individual's utility. As the Easterlin paradox has questioned the validity of GDP as a measure of progress and well being, measures of SWB based on subjective survey data have come to the attention of public policy makers as a complementary guide for policy. A systematic framework that explains why certain actions increase SWB and others do not, however, is missing.

This article argues that current models suffer from at least one of three problems: lack of a unifying theoretical framework based on the workings of the human psyche that can be reconciled with the data; static specification for both the dependent variable and/or independent variables;^[2] no account of individual heterogeneity. A theoretical framework based on evolutionary biology helps us understand where our preferences come from and how they are interrelated. Many of the decisions human beings take are not shaped by rational, conscious processes taking place in the orbitofrontal cortex, but by subconscious processes (Kahneman, 2011) in the limbic system. This article takes the view as is common in biology that many of the reward centres in our brain - presumably those areas that are associated with what may be called SWB - were shaped by evolutionary pressures.

An individual's SWB influences her behaviour today, i.e. human decisions are partially driven by emotions, moods and therefore also by SWB. As these decisions in themselves result in outcomes influencing SWB, omitting lags of SWB in the specifications could result in biases. Furthermore, dynamic specifications allow for the pivotal distinction between long-term and short-term effects, and are, therefore, essential for public policy makers.

Despite the universal mechanisms assumed in the theoretical framework, people are heterogeneous: the psychological determinants of SWB differ between individuals. To avoid biases arising from correlations of this heterogeneity and our independent variables, it is fundamental that panel data allows for unobserved, persistent individual effects.

Based on waves 8 to 18 of the BHPS this article provides empirical evidence of differential adaptation reference-dependence in domains not yet established in the literature and persistence of SWB.

This article argues that the empirical patterns reflect behaviour that was adaptive and functional in evolution, and introduces an evolutionary framework. This complements existing literature focusing on evolutionary efficiency of habit formation and peer effects (Rayo and Becker, 2007). This article will focus on an intuitive argument for differential adaptation and derives an evolutionary model for the persistence in SWB. Autoregressive and persistent happiness functions can be shown to be a superior mechanism for natural selection in comparison to static ones. Differential adaptation can be explained by considering the differential value for evolutionary fitness.

Recent research uses paradigms that are compatible with an evolutionary model: specifically, the reference-dependent preferences (RDP) approach was able to resolve the Easterlin paradox: the positive correlation between income rank and happiness in a cross-section within a nation and the ineffectuality of increasing average incomes on happiness over time (Di Tella et al., 2010). RDP posit that there is a preference-drift (Van Praag and Kapteyn, 1973), in that the individuals' reference-points change over time and only relative positions matter (Frank, 1985). Evolutionary theories maintain that hedonic states may be autoregressive (Bottan and Perez-Truglia, 2010): i.e. current happiness may depend directly on past happiness. The coefficients on lagged events in specific domains suggest adaptation, whereas lags of SWB indicate persistence (Bottan and Perez-Truglia,^[3] 2010).

There is a growing micro-econometric literature using panel-data based on an RDP framework of SWB focusing on adaptation of happiness to specific life-events (Lucas, 2007), income changes (Clark et al., 2008), health shocks (Dolan and Kahnemann, 2008) as well as the impact of unemployment (e.g. Winkelmann, 1998). The main conclusion thus far seems to be that 'adaptation patterns differ for various life events and for different domains' (Ferrer-i-Carbonell and Van Praag, 2008: 2). New models modelling the adaptation process have been developed recently (Bradford and Dolan, 2010), but, critically, no model is capable to explain the heterogeneous empirical patterns – i.e. no rationale is given as to why there is adaptation to some events and but not to others.

This article's findings with regard to differential adaptation are consistent with Di Tella et al. (2010) who are the first to analyse adaptation to social status, finding that there is adaptation to income but not to status changes. The ineffectuality of absolute income changes over time is corroborated by several studies. The evidence on peer effects, specifically the dependence of SWB on relative position is ample and growing and seems to generalize to different domains. Clark et al. (2008) demonstrate that comparison effects also occur in the social domain.

The evolutionary model

Rayo and Becker (2007) show that to characterise our preferences today we should think about the fitness-maximizing SWB function devised by natural selection.^[4] This can be interpreted as a principal agent problem: The principal is the process of natural selection and the agent represents an individual with a set of genes. The principal designs the SWB function of the agent to maximize the agent's probability of reproductive success. The agent is born with the SWB function designed by the principal and maximizes his level of SWB.

Crucially, the optimal SWB function is designed for the ancestral environment in which humans evolved. Presumably, we share most of the innate characteristics of our hunter-gatherer ancestors.^[5] Specifically, peer comparisons, habit formation and subjectivity based on prior expectations 'can be evolutionarily advantageous in the sense of improving the individual's ability to propagate his genes' (Rayo and Becker, 2007: 303). Rayo and Becker derive a theoretical model that shows that 'an organism's SWB function measuring the desirability of alternative decisions, can deliver a more precise measurement when it is based on relative, not absolute, stimulus levels.' This gives a rationale for domain-specific adaptation. It is problematic that this implies that adaptation is a universal phenomenon and seems inconsistent with the empirical literature that provides ample evidence of differential adaptation. ^[6] Crucially, this article's argument is based on similar theoretical assumptions, but gives a rationale why adaptation does not occur in specific domains.

Our model sets up a dynamic model to analyse internal dynamics in the SWB-function, i.e. it compares a static with an autoregressive SWB function. A simple model is derived to show that autoregressive SWB functions are more optimal than static functions for natural selection. The biological mechanisms behind this persistence and positive impact of past SWB are well documented: happy people are healthier, live longer, have a better immune system,^[7] are more productive (Oswald et al., 2009) and are more successful (Lyubomirsky et al., 2005). One has to think about the SWB function in terms of a motivation system that guided human behaviour so as to maximize our probability of survival, i.e. a utility function is given to the hunter-gatherers to guide them in their decisions. The more adaptive a SWB function the higher the probability to survive and to be successful at reproduction.

Assume that natural selection designs an optimal SWB function to guarantee that those agents with a more adaptive SWB function survive. We assume that due to a process of trial and error during natural selection the 'optimal' 'SWB function' will be chosen. However, it is important to note that the probability of reproduction of the agents is not only determined by the efficiency of their SWB function, but it is also affected by random errors^[8] that partially disguise the true efficiency of the SWB function.

Assume that there are many different agents of different types. The type is given by the 'efficiency' of the SWB function; however, the process of natural selection does not observe the true type, but only realisations of the type consisting of the true type and a random error given a static SWB-function. A high type indicates 'high' fitness, which translates into high probability of survival. This type is heritable: each agent's reproductive profile matches that of her parent. We assume that next period's number of agents is given by the following replicator dynamic:^[9] N_t+1=2S_t, where S_t < N_t is the number of agents that survive in period t. For simplicity, this model does not consider the influence of choosing one's mate, where those who have been happier in the recent past may seem more attractive and so have more opportunities to pass on their genes.^[10] Crucially, however, this constitutes a further way for natural selection to ensure that "the species" as a whole survives, as those with "adaptive SWB-functions" are likelier to reproduce.

Now assume that type θ_i, an element of the type space Θ, is uniformly distributed between ρ and γ, where -∞ < ρ < γ < ∞

Assume a dynamic stochastic multi-period model. For simplicity assume that the success in propagating the genes in a certain environment is given by the type which is independent of time plus a random error with expectation zero. We also assume that the random error is independent of type and serially uncorrelated and normally distributed.

Assume that there are N_t agents in period t. Assume that any agent only survives if a certain type-realization, i.e. type of agent i and random error of agent i in period t surpasses the threshold level of type-realization given by ξ_t.

ξ_t is a positive function of the number of agents, N_t and a function of the initial distribution of types given by g(Θ), where g is the uniform distribution with bounds ρ and γ. Denote the equilibrium value^[11] of ξ_t by ξ_t*. As resources, such as food are limited in our evolutionary setting, we assume that natural selection will make sure that only a proportion of the agents survive, i.e. the 'struggle for survival' increases with N_t or in other words S_t/N_t is a decreasing function of N_t. Also, the threshold level will depend critically on θ_i. For simplicity we only consider the simplest relationship, i.e. the higher the average type level, , the higher the threshold value of survival. This means that in our model, not the absolute level of type, but only the relative level matters for survival.

The simple static SWB function (mechanism 1, M₁) of natural selection determining survival of types in a given period T < ∞ is given by

So agent i in a given period T survives if and only if

and does not survive if

So the goal of the natural selection is to design a SWB function, such that only 'high' types propagate their genes. But given the random disturbances it is possible that for two agents with types θ_j > ξ_t* > θ_i the resulting outcome is given by

This induces an inefficiency as a type does not survive despite the fact that a weaker type has survived. Consider an autoregressive SWB function where the probability of success is given by the type, the random error and the past realizations, where G denotes the size of the history, i.e. the number of past observations and a is an optimal weighting factor chosen by natural selection and determines how this period's and the average of past period's observations are weighted. For simplicity "a" is assumed to be ½ for the rest of this section.

Assume that the process of natural selection observes the past observations; specifically it observes the actual realizations of the SWB function employed, i.e. type plus error. The autoregressive SWB-function (M2) uses agent i's history of past observations by using the average of past realisations

It is obvious that averaging errors distributed symmetrically produces a better estimate of the mean of the error than just one realisation.

Given that for every player there are past observations, G, then the past observations are important in singling out the high types: the sum of past errors of one individual's is given by:

This means that the influence of the random component converges to zero as G goes to ∞. This in turn implies that

In other words, introducing an autoregressive SWB function increases the efficiency of the SWB-function as it simplifies singling out high from low types. I argue that the autoregressive SWB function will result in higher average levels of types and a quicker convergence to equilibrium with high types. In other words, an autoregressive and persistent SWB function is evolutionarily more adaptive than a static one.

Given

But

Natural selection has a higher probability of recognizing the true type of an individual given M₂

so given a history of G periods, where G → ∞ we will see an 'efficient' outcome if

The model predicts that larger idiosyncratic errors per period result in a relatively better discrimination between high and low types by the autoregressive SWB function. Assuming that the idiosyncratic risk factors for our hunter-gatherers were large, the autoregressive function seems more suitable to 'quickly' separate 'high' from 'low' types. Thus, M2 reduces the probability of keeping low types alive and that of killing off high types.

Due to a lack of analytical tractability of the model, simulations are used to demonstrate that the mean type will be higher under an autoregressive SWB-function and that the convergence to this will be faster. Mathematica simulations confirm both and even show that the mean type under the autoregressive SWB-function will be higher than under the mean type under the static SWB-function. It can be seen that white noise is clearly more influential in the static SWB-function as convergence to steady state equilibrium is slower (Figure 1). An implication of the model is that efficiency rises with the coefficient on lagged SWB.

This article tests empirically for the statistical significance of the lagged coefficient of the SWB function and finds that the above outlined theoretical model is consistent with the empirical data, i.e. SWB functions are found to be autoregressive.

Moreover, this article argues that differential adaptation can be understood by considering evolutionary theory: Certain 'goods' were inherently useful for increasing the probability of reproductive success four our ancestral hunter-gatherers. Such goods had an intrinsic and long-lasting evolutionary value in terms of survival probability (Hamilton, 1964): e.g. social support network, trust, reciprocal altruism, health, stable environment and social status. This article claims that there will be no adaptation to these goods in terms of SWB. In evolutionary terms the non-adaptation to social status results from social status being the single most important factor determining reproductive success.

Other goods do not seem to have intrinsic value from an evolutionary perspective and are therefore prone to adaptation. Examples are goods igniting hedonic pleasure, such as consuming expensive food, and income above a certain threshold, as it tends to be used mainly for such 'hedonic consumption'. Those goods are by-products of the SWB functions devised by natural selection, in the sense that those with high probability of success were more likely to consume them. They did not, however, fulfil any adaptive function. This article conducts a series of adaptation tests to establish that adaptation occurs only in specific domains, but not in others. The evidence provided in section 4 is consistent with the dependence of adaptation/non-adaptation on evolutionary efficiency.

Empirical strategy and data

A pervasive feature of SWB models is the finding of serial correlation in the idiosyncratic error term. A possible solution to this problem is to employ dynamic panel methods (Piper, 2012).^[12] A linear dynamic^[13] specification based on Arellano and Bond (1991) will be used to test the hypotheses of the evolutionary model, namely that there will be differential adaptation according to the 'evolutionary' efficiency value, that reference points in several domains matter (Rayo and Becker, 2007) and that SWB is autoregressive rather than static. This means that this article tests the evolutionary model's predictions by testing both inter- and intra-individual comparison effects. The article uses a linear specification for simplicity, thereby assuming equidistance of the dependent variable, as is common practice.^[14] The reason for using a linear model results from the finding that the difference between results from ordered probit and logit models are negligible (Ferrer-i-Carbonell and Frijters, 2004). This also seems to hold true for dynamic panel data models.^[15]

Our model is as follows:

ΔSWB_it=ρΔSWB_i,t-1+{θ₁Δy_it+θ₂Δy_i,t-1}+{ϑ₁Δs_it+ϑ₂Δs_i,t-1}+ λΔR_it+πΔHD_it+{β₁ΔC_it+ β₂ΔC_it-1+α₁ΔSC_it+α₂ΔSC_it+ τΔX_it+ Δε_it

where

ΔSWB_it=SWB_it-SWB_i,t-1

SWB_it is the dependent variable, y_it is real income, s_it is the log of status, R_it is a vector of reference points. C_it is a vector of consumption goods, SC_it is a vector that measures the strength of the social network and X_it is a vector of control variables. Crucially, several lags are included to test for adaptation to income, status, consumption goods as well as social ties. Individual specific time- invariant fixed effects, η_i, allow for heterogeneity in the means of the SWB_it series across individuals. ε_it is a random disturbance term that is independent between individuals and serially uncorrelated by assumption.

As OLS estimation for an equation in levels would be biased, as SWB_i,t-1 is correlated with (η_i + ε_it), the data is 'first-differenced' such that the individual effects, η_i, are eliminated from the model. Δε_it is dependent on ε_i,t-1 and implies that the OLS estimate of ρ in the first differenced model are inconsistent. Consistent estimates, however, can be achieved if we instrument ΔSWB_i,t-1 with a variable that is both correlated with ΔSWB_i,t-1 and uncorrelated to Δε_it. We make the critical assumption that the initial conditions, SWB_i1, are predetermined, i.e. are unrelated with the subsequent disturbance terms ε_it for t=2,3,...,T.^[16]  Given serially uncorrelated errors and predetermined initial conditions the lagged dependent variable SWB_i,t-2 will not be correlated with Δε_it. Therefore, it is a suitable instrument for the first differenced equation (Arellano-Bond, 1991). The dynamic panel specification has a major advantage over standard fixed effects regressions as it allows for the instrumentation of endogenous variables.

We assume all regressors to be exogenous, except for income and marriage. The endogenous regressors are instrumented by their first differences. There is a potential endogeneity for income as there is evidence that high SWB is highly valued in the labour market and also that 'happier' people are more productive (Oswald et al., 2009). We also take care of potential endogeneity of 'marriage' because 'happier' people tend to be more likely to get married. As we include one lag of income, and marriage, they are instrumented by the 2^nd lag in levels respectively. We choose a health variable mostly capturing physical health to minimize the potential endogeneity of health and SWB. Our health variable is a binary variable indicating whether someone was in hospital (as an in-patient) in the past 12 months.^[17] A variable that captures health clearly also captures mental health which would cause endogeneity bias. Importantly, in the fixed effects regressions we use clustered standard errors at the regional level as the reference points in the regression are calculated at a more aggregate level than the dependent variable.^[18]

We test 3 major hypotheses related to the evolutionary theory: namely, we test for adaptation in several domains. Based on the evolutionary model we would argue that some of these goods had a high "evolutionary" efficiency value, so we expect non-adaptation for these, whereas we expect adaptation to goods with low evolutionary efficiency value.

We argue that consumption in leisure activities, which may result in a higher quality of the social network, is 'evolutionary efficient', so we expect non-adaptation, whereas there will be adaptation to goods that merely ignite hedonic adaptation. This article also tests for adaptation of social relationships and hypothesizes that non-adaptation will be the case. We test whether reference-dependence occurs in domains other than income and status. Lastly, we test whether SWB is indeed autoregressive or not.

The data comes from the British Household Panel Survey (BHPS), a nationally representative panel of household- and individual-level data in Great Britain, which started in 1991 with currently 18 available waves. The article uses waves 8 to 18^[19] of the BHPS between the years 1998 and 2008 offering rich information on sociodemographic, occupational, political, value-related, and SWB variables. Each household is interviewed in successive waves, with new members interviewed as part of the existing household, and any departing members as part of a new household. This article is based on an unbalanced panel with 41154 observations and 9530 individuals.^[20]

Single-item scales of SWB as commonly used in the literature have the disadvantage of lower reliability. Therefore, this article reverts to a commonly used multi-item scale, the GHQ-12, General Health Questionnaire. It consists of 12 questions, via a self-completion questionnaire, covering, amongst others, feelings of strain and lack of confidence. Crucially, this measure captures a slightly different concept that focuses on stress in comparison to the usual single-item measure. Responses are made on a four-point scale of frequency of a feeling in relation to a person's usual state. The GHQ^[21] is used in psychological and economic research, and is deemed a robust indicator of the individual's SWB. In this article we aggregate the GHQ subscales, and the count is reversed and shifted to the positive domain so that higher scores indicate higher levels of SWB.^[22]

Status, Income, Consumption expenditures, Social Ties

Status conceptualised as an individual's relative standing to others is captured using the Standard International Occupational Prestige Scale (SIOPS). SIOPS is an independent score given to each person's job (Ganzeboom and Treimann, 1996). Status is calculated in two steps: first, the International Standard Classification of Occupations (ISCO88) of the International Labour Office is used to determine the occupation. Secondly, the occupation is assigned a prestige score. The ISCO88 system categorises occupations into a hierarchy that tries to capture two dimensions: specialisation and skill level. The SIOPS scale (Treimann, 1977) uses the results of surveys on prestige evaluations of occupations.^[23] The score is based on rankings of occupations by survey respondents based on evaluations of status, worth, goodness, and power. Monthly p.c. log household income deflated by CPI is also included in the data. Three household level consumption variables indicating how much the household spends on food, eating out, and expenditure on leisure activities are contained in the dataset. Social ties are measured by self-reported frequency of talking to neighbours and self-reported frequency of meeting people.

Four different reference points to capture comparison effects are included: the average SWB in a certain region, the average log-status in a certain region, the average log of monthly household income in a region and the average self-reported frequency of meeting people in a certain region. There are 19 regions in the BHPS. The vector of control variables consists of individual characteristics: Marital status, employment status, and educational achievement. We also control for number of children, age, and maternity leave. Four dummy variables indicating behaviour typically exhibited by hyperbolic discounters, i.e. individuals with present-biased preferences, were included: 'health problems due to alcohol or drugs', 'housing payments required borrowing or cutbacks', 'not-saving' and the dummy variable 'smoking'.

Results

The regression results^[24] for a selection of key variables are presented in Table 3.

Consumption Expenditures: the article finds the contemporaneous coefficients of 'money spent eating out' and household expenditure on food to be insignificant, whereas the coefficient on the lag is negative and significant, i.e. the null hypothesis of non-adaptation can be rejected. This indicates that the long-term effect of eating out is negative, maybe due to an increase in the aspiration level. An alternative interpretation might be that materialism and desires for hedonic pleasures (food) are negatively associated with SWB.

Contrary to this, the amount spent on leisure has a positive and statistically significant effect on SWB and the lag coefficient on the amount spent on leisure is insignificant, i.e. there seems to be no evidence in favour of adaptation. This could be attributed to the fact that 'leisure activities' may constitute a good proxy for the strength of the social network. These findings are highly interesting as it shows how after all 'consumption' decisions are shown to affect SWB in different ways. Clearly, this article argues that 'consumption' that invests in social activities rather than in hedonic pleasures will eventually result in higher levels of SWB.

A variable capturing the social ties with the respondent's neighbours, namely the frequency of talking to neighbours, is tested and found to positively affect SWB without adaptation effects; On the other hand, the frequency of meeting people is insignificant does not affect SWB. It is interesting to see that, again, people do not adapt to changes in a variable that measures the strength of the social network.

The coefficient of the status variable is positive and lags on status are insignificant so that we do not reject the null hypothesis of non-adaptation to social status, which underlines that Di Tella et al.'s (2010) findings generalise to the BHPS. This means that increases in social status, as measured by SIOP, result in increases of SWB and most importantly people do not adapt to those. It is crucial in this context to differentiate between the estimates obtained by instrumenting the income variable and the fixed effects regressions using the same specification: While the fixed effects regressions confirm the adaptation hypothesis that the contemporaneous coefficient of income is significant and positive and the lagged coefficient negative and significant and more than offsets the contemporaneous effect, the results for the A-B estimator are quite different: Once income is treated as an endogenous variable and instrumented accordingly the estimates of both the contemporaneous and lagged coefficient are insignificant (Table 4). This is an interesting finding as the estimates of the contemporaneous coefficient of income, not taking account of endogeneity of income, may be upward biased. Interestingly, the same is true for the dummy variable indicating whether an individual is married or not. In fixed effects regressions we find that the variable is highly significant and that there is partial adaptation to this positive effect. However, once we instrument this variable and treat it as endogenous it becomes insignificant.

This is compatible with the finding that most of the happiness-marriage correlation is due to the happy being more likely to marry (Stutzer and Frey, 2006)

The econometric problem in this sense is that many variables correlated with high SWB are also highly correlated with high income, such that the statements the coefficient on income is insignificant and people with high income have higher SWB are not contradictory. An evolutionary perspective shows that trying to establish causality might be misleading, as income, marriage and SWB and other variables may have common causes. Thelag on SWB is positive and significant indicating that SWB follows an AR (1) process.^[25] The robustness of this finding is corroborated by the result being invariant as to whether the multi-item scale of SWB or a single-item scale of SWB was used (Table 5). So the autoregressive nature of the process can no longer be attributed to a possible lack of validity and reliability of the single-item dependent variable, as proposed by Bottan and Perez-Truglia (2010). The positive feedback mechanism of past SWB is usually rationalized as follows: Happy people are healthier, live longer (Veenhoven, 2008),^[26] are more productive (Oswald et al., 2009), and more successful (Lyubomirsky et al., 2005). The article extends the approach of Luttmer (2005) and uses four different reference points on the regional level to capture comparison effects.

We find evidence that SWB is contagious: specifically, the higher the SWB in a certain region the higher the individual's SWB. Importantly 'unobservables' associated with the higher average SWB in a region could result in more positive relationships among the people in a specific region. Also the region in which a person lives might be endogenous, as people with higher levels of SWB would prefer to choose to live in a region with higher levels of SWB. As the regions captured by the BHPS are relatively large, the endogeneity of mean SWB in a region is not very problematic. The coefficient on average status and log-income in a region is statistically insignificant, which stands in contrast to the findings in the US (Clark and Oswald, 1996). We find evidence of comparison effects in the social realm: the average reported frequency of meeting people is found to be significant with a negative coefficient, indicating that these social aspiration levels exert an impact on SWB. This finding is in line with Clark (2008) who finds comparison effects in several domains. It is important to note that the regions in the BHPS may be potentially too large to capture comparison effects.

It is important to assess the relative size of coefficients (Dolan and Kavetsos, 2012). In our model the size of the lagged coefficient is quite prominent, which underlines the importance of the intrinsic dynamics in SWB. Crucially, the coefficients of many of the significant lagged variables are very comparable in size to the coefficients on the respective contemporaneous variables corroborating the claim that intra-individual reference-dependence is important.

The Kernel Density estimate, which compares the distribution of residuals in the model with the normal distribution, provides evidence of deviations from a normal distribution with little distribution mass at the tails and a significant amount centred around the mean (kurtosis < 3). However, the deviation from normality is not immense, as can be seen by comparison by comparison of homo- and heteroskedastic standard errors in table 4. The Arellano-Bond test for zero autocorrelation confirms our lag structure. Serial correlation in the first-differenced errors at an order higher than one implies invalid moment conditions (Table 6). The test statistic indicates that this is not the case, as the 2^ndorder differenced-error autocorrelation is rejected. The results are robust to using different dynamic panel estimation techniques, as comprehensively evidenced in table 4. Using different instruments, as suggested by the systems approach (Arellano and Bover, 1995; Blundell and Bond, 1998), only marginally changes the results and increases the efficiency of the estimators. The results also remain robust when we use homoscedastic standard errors. The null hypotheses of the overidentifying restrictions being valid, is not rejected by the Sargan test statistic, although heteroscedasticity biases the Sargan test towards rejecting the null hypothesis (Table 7). Furthermore, most findings are robust to using static fixed effect regressions. However, due to the omission of the lagged dependent variable in the static fixed effects approach, the coefficients in the latter seem to be upward biased as highlighted in Table 4. A Hausman test for attrition bias comparing the coefficients of the unbalanced panel with a perfectly balanced panel (that drops all individuals who did not respond to the survey at least once) indicates no systematic difference (Table 9).

Conclusion

This article argues that the evolutionary setting may be important for our understanding of SWB. This simple evolutionary framework shows that for example income, SWB and health may have common causes, which stands in stark contrast to the idea that changes in one of the domains results in changes in another.

The dynamics in SWB seem more complicated than assumed thus far in the literature: There is an unspecific persistence effect that makes people with currently high SWB likely to exhibit high SWB tomorrow, but there are adaptation effects that make people with high derived SWB from a specific domain likely to derive less SWB from that domain. The omission of unspecific internal dynamics in SWB can be interpreted as a misspecification of past models so that the robustness of the old adaptation tests (Lucas, 2007) needs to be reconsidered.

In summary, this article makes two theoretical contributions. Firstly, it derives a model that shows why an autoregressive and persistent SWB function is more evolutionarily efficient than a static one. The article opens the possibility that (non-)adaptation patterns can be understood in evolutionary terms: This means that there are some goods with intrinsic value for evolutionary efficiency (social status, a friendship network), whereas other goods do not have intrinsic value for evolutionary efficiency (income, food consumption). Secondly, it contributes to the empirical literature with three findings: First, the article provides evidence of differential domain-specific adaptation. There is adaptation to expenditure of eating out and food expenditure, but there is no adaptation to expenditure on leisure activities, social status as well as the frequency of meeting neighbours. Secondly, SWB is found to be autoregressive and persistent for both a single-item scale and multi-tem scale. Lastly, the coefficient of the mean of SWB in a certain region is positive, suggesting that SWB may be 'contagious', whereas the coefficient of average frequency of meeting people in a certain region is negative, indicating comparison effects in the social realm.

---

Acknowledgments

First of all, I would like to thank Peter Hammond, Jennifer Smith and Jeremy Smith for their fruitful feedback and advice. Two anonymous referees' excellent comments and detailed suggestions for improvement are highly appreciated. I am grateful to Wiji Arulampalam, Giana Boero, Rumen Kostadinov, Nikita Orlov, Andrew Oswald, Maximilian Pesch and André Sieverding for their insightful comments and support. I also want to thank all conference participants at the Carroll Round 2012 at Georgetown University as well as participants at the Centre of Longitudinal Studies Conference at the Institute of Education in London. This article was written during my studies at Warwick University and would not have come into existence without the great environment of Warwick Economics Department. The biggest thank goes to my family for their support. Any remaining errors are mine.

List of figures

Figure 1a Average type under the autoregressive and static SWB-functions: 'Mathematica' simulation^[27]

Figure 1b: Simulation with a different parameterisation

List of tables

Table 1: Key summary statistics

Table 2: Summary statistics of the independent variable

Table 3: Results of the Arellano- Bond Dynamic Panel Data Estimation

Table 4: Results from different estimation techniques

Table 5: Single-item measure – multi-item-measure

Table 6: Arellano-Bond test for zero autocorrelation in first-differenced errors

Table 7: Sargan test of overidentifying restrictions

Table 8: More elaborate variable descriptions

Table 9: Hausmann Test for Attrition

Appendix

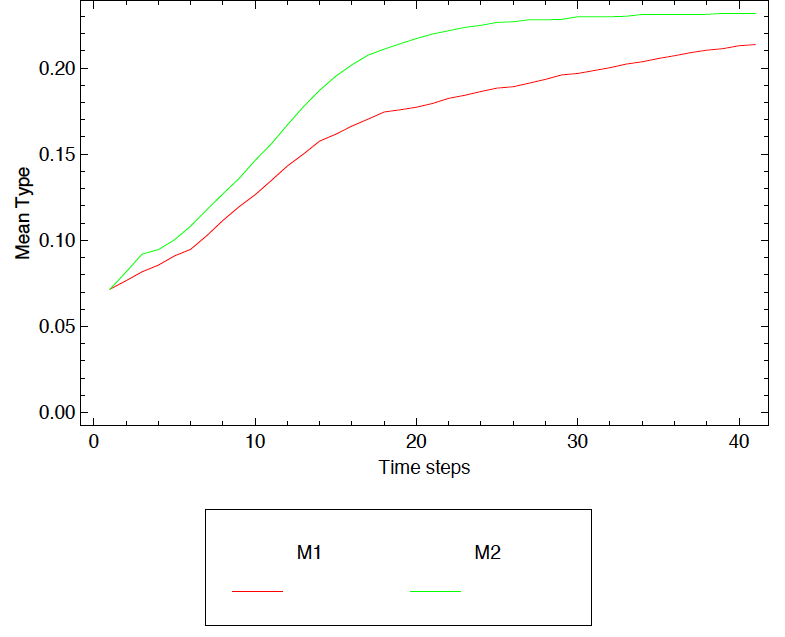
Figure 1a: Average type under the autoregressive and static SWB-functions: 'Mathematica' simulation

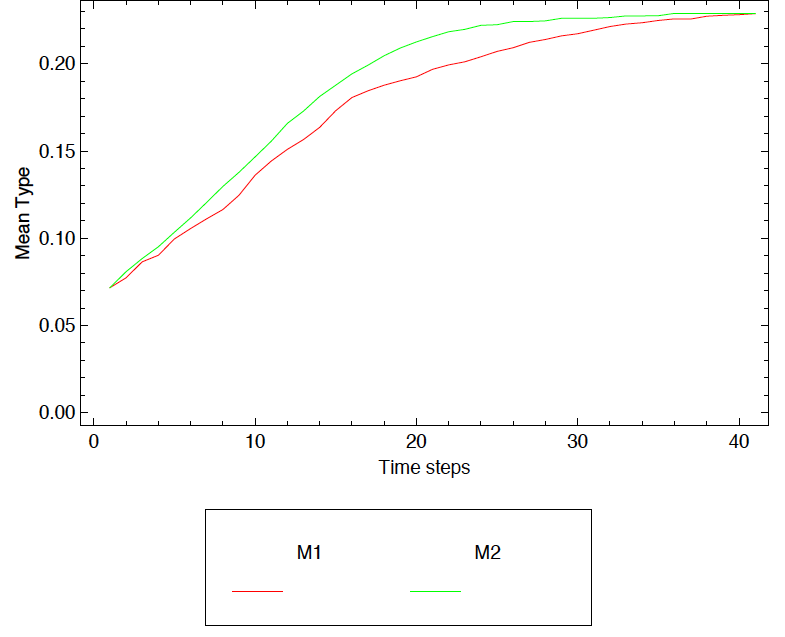
Figure 1b: Simulation with a different parameterisation

N=56114	Variable		Mean	Std. Dev.
	GHQ		25.14	5.13
	Subsample	N	Mean GHQ	Std. dev.
Gender	Male	28116	25.79	4.71
	Female	27998	24.49	5.46
Marital status	Married	32512	25.15	4.92
	Divorced	5198	24.71	5.50
	Separated	1181	23.67	6.43
	Widowed	796	24.23	6.051
	Never married	16268	25.41	5.25
Employment status	Employed	45809	25.18	5.03
	Unemployed	964	22.40	7.01
	Self-Employed	5753	25.51	4.729
	Retired	874	25.87	5.176

Table 1: Key summary statistics

N=56114
Status	Overall	42.41	13.84
(Measured by SIOP)	Between		12.67
	Within		6.31
Married	Overall	0.57	0.49
	Between		0.47
	Within		0.17
Mean SWB in a region	Overall	25.15	0.30
	Between		0.25
	Within		0.18
Mean status in a region	Overall	42.41	1.61
	Between		1.56
	Within		0.51
Log mean real income	Overall	3.37	0.14
In a region (in a given year)	Between		0.12
	Within		0.07
Mean frequency of meeting	Overall	3.29	0.093
People	Between		0.084
	Within		0.045
Expenditure on meals	Overall	5.04	3.18
Spent eating out	Between		2.74
	Within		1.87
Expenditure on food	Overall	6.94	2.07
	Between		1.86
	Within		1.13
Expenditure on leisure	Overall	4.61	3.34
	Between		2.87
	Within		1.98
Frequency of talking to neighbours	Overall	2.96	.096
	Between		0.85
	Within		0.59
P.c. log real household income	Overall	3.35	0.67
	Between		0.60
	Within		0.40

Table 2: Summary statistics of the independent variable

Variable	Coef .	Std. Err.	t-value	P value
Autoregressive component
Lag of SWB	.111	.011	9.65***	0.000
Status variables
Status (log)	.008	.004	2.03**	0.042
L1.	-.059	.004	1.50	0.113
Status (log) last year	.0005	.0002	2.35**	0.019
Expenditure on leisure	.0436	.012	3.42***	0.001
L1.	-.001	.011	-0.870	0.598
Expenditure on food	.007	.032	0.22	0.862
L1.	-.076	.037	-2.04**	0.042
Expenditure on eating out	.006	.014	0.45	0.653
L1.	-.038	.012	-3.01***	0.003
Regional reference points
Mean SWB	.998	.133	7.47***	0.000
Mean income	-2.12	.1.359	-1.57	0.117
Mean frequency of meeting people	-1.40	.553	-2.54***	0.011
Mean Status	-.086	.067	-1.29	0.517
Real income (in logs)	2.336	.1.622	1.46	0.145
L1.	-.387	.669	-.580	0.563
Freq. of talking to neigbours	.075	.037	2.02 **	0.043
L1.	.009	.0368	0.26	0.0798

Table 3: Results of the Arellano- Bond Dynamic Panel Data Estimation
*** significant at the 1% level; ** significant at the 5 % level, * significant at the 10 % level

Variable	1) A-B heteroskedastic	2) A-B homoscedastic	3) Systems Approach	4) Fixed Effects Clustered SEs
Number of observations	41145	41145	56114	56773
Autoregressive component
Lag of SWB	.111*** (.013)	.111*** (.011)	.120*** (.006)
Status variables
Status (log)	.0086** (.289)	.0086** (.0042)	.009** (.005)	. 0063** (.0022)
L1.	-.0059 (.0039)	-.0059 (.0037)	-.005 (.0036)	-.0064** (.0023)
Status (log) last year	.0005** (.0002)	.0005** (.0002)	.0005** (.0002)	.0003*** (.0001)
Hyperbolic discounting and financial capability
Financial capability 1	-.556 (.352)	-.556** (.026)	-.649** (.250)	-.948*** (.025)
Financial capability 2	-.566*** (.201)	-.566*** (.169)	-.626*** (.159)	-1.03*** (.129)
Smoker	-.133 (.160)	-.133 (.145)	-.095 (.140)	.193 (.144)
Not saving	-.130 (.089)	-.130 (.085)	-.171** (.075)	-.2441*** (.058)
Health prob:alcoholdrugs	-1.84 (1.17)	-1.84*** (.0679)	-1.85*** (.668)	-1.751*** (.747)
Consumption variables
Expenditure on leisure	..0436*** (.0133)	.0436*** (.012)	.0477*** (.012)	.0523*** (.010)
L1.	-.001 (.012)	-.001 (.011)	-.001 (.011)	-.0046 (.009)
Expenditure on food	-.007 (.035)	-.007 (.032)	.0263 (.032)	.0550*** (.0144)
L1.	-.076* (.0420)	-.076** (.037)	-.0749** (.0296)	-.0606** (.016)
Expend. on eating out	.006 (.014)	.006 (.0144)	.011 (.013)	.0291*** (.007)
L1.	-.038*** (.013)	-.038*** (.0127)	-.036*** (.0121)	-.0269*** (.008)
Regional reference points
Mean SWB	.998*** (.137)	.998*** (.133)	1.03 ** (.127)	.916*** (.082)
Mean Frequency of meeting people	-1.40*** (.571)	-1.40*** (0.553)	-1.23*** (.525)	-.853*** (.380)
Income variables
Real income	2.366 (1.818)	2.366 (1.622)	1.165 (1.164)	.113** (.051)
L1.	-.387 (.737)	-.387 (.669)	-.244 (.477)	-.1300*** (.044)
Social ties
Freq. of talking to neigbours	.075* (.040)	.075** (.037)	.073** (.036)	.0664*** (.027)
L1.	.009 (.038)	.009 (.0369)	.005 (.035)	.016 (.020)

Table 4: Results from different estimation techniques
*** Significant at the 1% level; ** significant at the 5 % level, * significant at the 10 % level
1) Main regression is based on the linear Dynamic Panel Data model by Arellano-Bond (1991) with robust standard errors (Table 3)
2) Main regression with homoscedastic standard errors
3) Systems Approach: Dynamic Panel Data Model based
4) Static Fixed Effects Panel Data model

Arellano-Bond Dynamic Panel Estimation			Number of observations=27701
Group Variable: pid			Number of Groups=7777
Time variable: year
number of instruments = 73			Wald chi2(55) = 282.69
One Step Results			Prob > chi2 = 0.000
		Robust
	Coef.	Std. Err.	z	p > z
Lfsato
L1.	0.072	0.0146	4.97	0.000

Table 5: Single-item measure – multi-item measure
AR(1) process with positive lagged dependent variable also for the single-item scale:
Robustness of results corroborated by persistence in the lagged single-item scale dependent variable given by:
How satisfied are you with your life overall? (On a scale from 1 - Not satisfied at all, 7 - completely satisfied)

Order	z	P-value
1	-18.915	0.000
2	-.79484	0.4267

Table 6: Arellano-Bond test for zero autocorrelation in first-differenced errors
H0: no autocorrelation in the errors

Sargan test	χ2	Prob > χ(27)2
	31.45461	0.2529

Table 7: Sargan test of overidentifying restrictions
H0: Overidentifying restrictions are valid

The 12 questions used to create the GHQ-12 measure appear in the BHPS questionnaire as follows: Here are some questions regarding the way you have been feeling over the last few weeks. For each question please ring the number next to the answer that best suits the way you have felt.

Have you recently

a) been able to concentrate on whatever you're doing? Better than usual (=1), Same as usual (=2), Less than usual (=3), Much less than usual (=4)

b) lost much sleep over worry?, e) felt constantly under strain?, f ) felt you couldn't overcome your difficulties?, i) been feeling unhappy or depressed?, j) been losing confidence in yourself?, k) been thinking of yourself as a worthless person? with the responses: Not at all (=1), No more than usual (=2), Rather more than usual (=3), Much more than usual (=4)

c) felt that you were playing a useful part in things?, d) felt capable of making decisions about things?, g) been able to enjoy your normal day-to-day activities?, h) been able to face up to problems?, l) been feeling reasonably happy, all things considered? with the responses: More so than usual (=1), About same as usual(=2), Less so than usual (=3), Much less than usual (=4)

Regional Variables:

There are 19 regions in the dataset: 1) Inner London, 2) Outer London, 3) Region of South East, 4) South West, 5) East Anglia, 6) East Midlands, 7) West Midlands conurbation, 8) Region of west midlands, 9) Greater Manchester, 10) Merseyside, 11) Region of North West, 12) South Yorkshire, 13) West Yorkshire, 14) Region of Yorks & Humberside, 15) Tyne & Wear, 16) Region of North, 17) Wales, 18) Scotland, 19) Northern Ireland

Individual-specific control variables:

Marital status; Married, divorced, widowed, separated.

Employment status: Dummy variables are introduced in the model: Whether someone is unemployed, on maternity leave, is currently in paid employment, in retirement (retired) or is self-employed (selfempl)

Educational achievement: Whether someone obtained a High degree, first degree, is still at school, has not acquired a formal qualification, has completed an apprenticeship, has achieved another "high qualification", a teaching qualification or another "vocational qualification".

We also control for whether the respondent has been in hospital last year (approximation for physical health), cares for a handicapped person in the household number of children and age & age2.

Furthermore, a dummy variable indicating whether an individual cares for handicapped person in the household is included in the regression.

Consumption Variables (household level variables):

1) Amount spent on leisure per month: 13 categories (1: Nothing, 2: Under 10, 3: 10-19, …,12: 140-159, 13: More than 160)

2) Total weekly food |and grocery bill: 13 categories (1: Nothing, 2: Under 10, 3: 10-19, …, 12: 140-159, 13: More than 160) 3) Amount spent |eating out per |month: 13 categories (1: Nothing, 2: Under 10, 3: 10-19, …, 12: 140-159, 13: More than 160)

3.6 Social Ties:

Measured by the variables "frequency of talking to neighbours" as well as "frequency of meeting people" measured on a five point scale (5: on most days, 4: once or twice a week, 3: once or twice a month, 2: less than once a month, 1: never)

3.7 Reference Points: The paper additionally constructs a 5 reference points: Mean income /status /SWB /frequency of meeting people.

Table 8: More Elaborate Variable Descriptions

Hausmann test	χ2	Prob > χ(72)2
	64.22	0.7314

Table 9: Hausmann test for attrition
H0: difference in coefficients not systematic

Notes

[1] Christopher Roth, from Heidelberg, Germany, is reading for an M.Phil. in economics at Oxford after having completed his undergraduate studies in economics at the University of Warwick in 2012. His research interests are situated at the intersection of economics and psychology with a specific focus on developing economies and well-being. He is currently working on social networks and consumption decisions with data from Indonesia. He intends to pursue a Ph.D. after the completion of his M.Phil. in 2014.

[2] It is pivotal to include both lagged independent and dependent variables, as the comparison effects can only be appropriately modelled if both the unspecific persistence effects as well as the domain-specific comparison effects (conditional on lagged SWB) are taken into consideration.

[3] They use a single-item measure of SWB and argue that their persistence results constitute an artefact of the low reliability of their dependent variable.

[4] A teleological fallacy of this model is avoided, provided we recognise that the evolutionarily stable goal is something like the probability of long run survival.

[5] Even though the environment we live in has changed so that the SWB functions may be suboptimal in today's world.

[6] For example, non-adaptation to unemployment.

[7] The field of positive psychology has accumulated a vast amount of evidence in favour of this claim.

[8] One should think about those risk factors as idiosyncratic risk factors present in natural selection.

[9] Those surviving have one offspring.

[10] It would be possible to introduce marriage by making S the probability of surviving into marriage, rather than just surviving.

[11] The equilibrium level is determined by the data on types, distribution of types and number of individuals.

[12] By repeated substitution, it can be demonstrated that through the lagged dependent variable dynamic specifications contain the entire history of the independent variables (Piper, 2012).

[13] Results resemble fixed effects estimates, although the latter seem to be upward biased due to the omission of the lagged dependent variable and as endogenous variables are not treated as such.

[14] The difference on the SWB scale between 12 and 13 may be much smaller than that between 26 and 27. Equidistance implies additivity and intra- and interpersonal comparability and consistency of survey responses.

[15] Results concerning persistence of SWB similar to Orlov (2011) who uses a non-linear semi-parametric dynamic specification.

[16] The correlation between the fixed effects and SWBi1is left unrestricted: there is no necessity for any stationarity condition to be satisfied.

[17] Assuming that most people who go to hospital do so due to physical problems, but not psychic ones. This assumption clearly neglects psychiatric morbidity.

[18] Cluster the standard errors at the level of the most aggregated right-hand side variable. For the Arellano-bond dynamic panel estimation clustering of standard errors at a level other than individual is non-trivial. The clustering in the fixed effects regressions did not substantially change the results.

[19] Many relevant consumption variables as well as variables from the social realm only became available at the beginning of wave 8.

[20] Observations were lost as some individuals did not respond to all of the relevant variables from the model and due to the inclusion of lagged dependent and independent variables.

[21] Also, the GHQ avoids the problem presented by the life satisfaction question in the BHPS, as it is not asked in the middle of the survey questionnaire.

[22] Running from 0 (responses indicating lowest SWB) to 36 (responses indicating high SWB).

[23] Conducted in approximately sixty countries.

[24] The paper also finds that several variables capturing the concept of hyperbolic discounting are significant and positive. Additional results offered on request.

[25] This result seems robust and is corroborated by the output of the test of autocorrelation in the errors.

[26] The field of positive psychology has accumulated a vast amount of evidence in favour of this claim.

[27] I am happy to provide the code for different simulations that demonstrate the robustness of results.

[28] JEL classification: I31, D0

 

References

To cite this paper please use the following details: Roth, C. P., (2013), 'Darwin's Happiness Hypothesis: Subjective Well-Being in an Individual Panel from an Evolutionary Perspective,' Reinvention: an International Journal of Undergraduate Research, Volume 6, Issue 1, www.warwick.ac.uk/reinventionjournal/issues/volume6issue1/roth Date accessed [insert date]. If you cite this article or use it in any teaching or other related activities please let us know by e-mailing us at Reinventionjournal at warwick dot ac dot uk.