Households are a natural unit for epidemiological data collection: many studies of (particularly respiratory) diseases recruit everyone sharing living arrangements at one address.

Household epidemic dynamics can be modelled exactly using methods from applied probability. At present there are two options: where immunity is long-lasting, arbitrary recovery-time distributions can be modelled using sophisticated techniques like imbedding; where individuals can become susceptible again following recovery, a continuous-time Markov chain with a self-consistent term is appropriate.

These household type models have been applied to pandemic influenza and are being used to understand RSV (Respiratory Syncytial Virus) control.

Much of the code we have written on this is available via the EpiStruct website.

There are three main applications of household modelling that have been considered by researchers in WIDER:

Dynamics

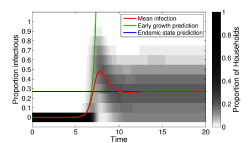The transient dynamics of a household-structured model are often quite different from non-household dynamics (as shown on the left). This is due to the strong transmission that occurs within the household compared to the weaker transmission between them. In essense the household acts to amplify infection.

Interventions

Two main issues have been considered:

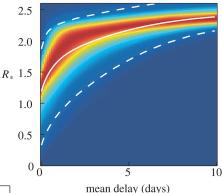• Vaccination can be optimised on the basis of household structure; this expands on the work of Frank Ball and coworkers and we have begun to think when "equalising susceptibility" is optimal. In addition, some assumptions about that action of vaccines that are equivalent in non-household-structured populations have distinct consequences when households are modelled. The figure on the right shows the impact of the mean delay between infection and action of antivirals on the between household reproductive number, R*.
  
• Household structure provides a useful target for reactive control measures, such as distribution of anti-virals. Using cutting-edge tools and latest data, our work has shown how the delay in delivering antivirals can have a substantial impact on the level of control that can be achieved.
  

Inference

Working with household-stratified data allows for the inference of far richer sets of epidemiological parameters than can be inferred from population-level data. In particular we are interesting in understanding how transmission scales with household size and household composition -- clearly not all links within a household are equal, but can we measure these heterogeneties and utilise them to target controls.

---

Publications

A. Black, T. House, M.J Keeling, and J. V. Ross (2013) Epidemiological consequences of household-based antiviral prophylaxis for pandemic influenza. Journal of the Royal Society Interface 10( 81) (2013) 20121019

House, T., Ross, J.V., Sirl, D. (2013) How big is an outbreak likely to be? Methods for epidemic final-size calculation. Proceedings of the Royal Society A 469 (2150), art. no. 0436

J. V. Ross, T. House and M. J. Keeling, "Calculation of disease dynamics in a population of households," PLoS ONE 5:3 (2010) e9666.

T. House and M. J. Keeling, "UK household structure and Infectious Disease Transmission," Epidemiology and Infection 137 (2009) 654-661.

T. House and M. J. Keeling, "Deterministic epidemic models with explicit household structure," Mathematical Biosciences 213 (2008) 29-39.

Funded by: EPSRC, MRC

WIDER people Involved:

Matt Keeling

Thomas House

Lorenzo Pellis

Tim Kinyangui

External collaborators:

Joshua Ross (Adelade)