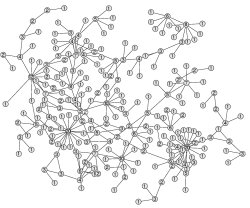
Networks are a powerful tool for conceptualising the potential interactions within a population that can lead to the spread of infection. Networks allow us to capture three important aspects of the interactions that lead to transmission (i) frequent interaction with a few individuals within a large population (ii) large variations (between individuals) in their number of contacts (iii) clustered nature of contacts -- such that networks form cliques.

Related work considers the implications of livestock movement networks for the transmission of infections, particular bovine TB and endemic Foot-and-Mouth Disease.

Pairwise models

Spatial heterogeneity is vitally important to the dynamics and persistence of many biological populations. Often this spatial heterogeneity can be a reflection of variations in the underlying distribution of resources. However, a secondary cause of spatial heterogeneity is the interaction between organisms leading to spatial correlations; a good example of which is the spread of infection through a network.

Traditionally, such spatial structure was only reproduced by complex spatial models, more akin to simulations than mathematical equations. In recent years however a series of tools has been developed to directly model the spatial correlations that can arise when discrete organisms interact with their local environment. One of the simplest type of such models is the pair-wise model, where instead of modelling the number of individuals, the number of interacting pairs is modelled by a set of differential equations.

This framework is particularly useful for understanding the spread of diseases, where a contact network determines who interacts (and therefore can infect) whom. A mixture of analytical and numerical studies have shown that including the correlations that develop within this network structure can have strong quantitative (as well as qualitative) effects.

Recent work shows that pairwise models give accurate predictions for SIR-type models on unclustered networks. On-going research aims to extend these results to clustered networks and SIS-type dynamics. Both of these are extremely complex due to the multiple feed-backs that occur.

Measurement of contact patterns

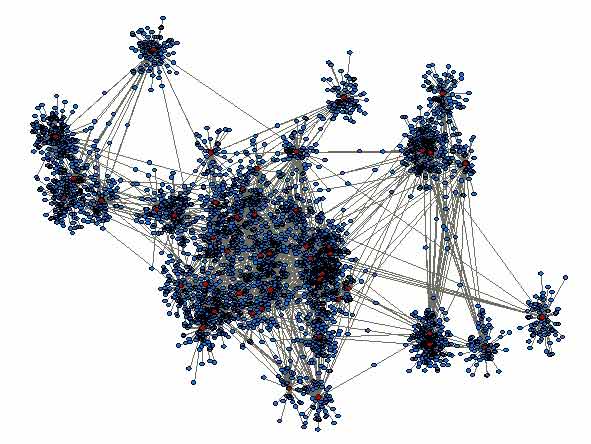
Generally, very little is known about the mixing patterns that facilitate the transmission of diseases. This is particularly so for diseases which spread through social contact, whether it is via airborne droplets or through closer contact, such as touch. Influenza, smallpox, the common cold, SARS, and MRSA are all infections that spread through social interactions. Quantifying social networks, from the viewpoint of infections, is therefore important to predict the spread of possible pandemic infections and to predict the effectiveness of various social control measures.

The number of people (degree) encountered by an infectious person during a day is important for disease transmission, and at the scale of the population can ultimately determine whether an outbreak occurs. Most mathematical models of infection include this measure, yet very little is known about it for human populations and societies. In addition, how frequently individuals see people (contacts) during the period for which they are infectious, and the relationship between these contacts, also determine the rate at which a disease can spread though a group of friends, a school or workplace, or even a city or country. For more information see the Contact Survey pages.

Synthetic populations

To fully specify the dynamics of a disease through a network, it would be ideal to survey the entire population and understand where and what each person in the population is doing at every moment of the day. This is however patently impossible, due to many factors such as the cost that to gather this information would incur and also ethical issues such as invasion of peoples privacy.

As a step in this direction, whilst avoiding the issues mentioned above, it is possible to create a synthetic population. The idea of a synthetic population is that rather than having information on each person in your population, you can generate a population of similar size and with similar characteristics using available data sources (such as census and time use surveys). In the synthetic population, "people" are assigned with demographic information, live in households of a certain size where they will make contact with other members of the household, and workplaces/schools where they will make contacts with others at the same location.

One of the main uses for such a population would be to choose the best intervention from a list of given interventions that could be implemented during an epidemic. As the synthetic population is assumed to have similar characteristics as the true population, these results can be used in the event of a epidemic taking place in the real world and can therefore be used to inform medical policy when the need arises for these decisions on intervention to be made.

Along with the use of these populations towards simulation of epidemics, once we have this population it is possible to use it in many other situations. There are many scenarios where having a population of people with demographic data assigned to them, who live in households in given areas, and work at certain locations, would be useful. Examples of this would be consideration of the affect of road closures on the movement of citizens and the potential risk to life of a chemical leak or biological incident emanating from a specific source.

Funded by BBSRC, DTI/HO, EPSRC, EU, NIH, Leverhulme, Wellcome.

 

WIDER people involved:

Matt Keeling

Thomas House

Lorenzo Pellis

James Nokes

Matt Graham

External collaborators:

Jon Read (Liverpool)

Leon Danon (Queen Mary's)