Regression to the mean
A policy proposal recently put forward by Nick Clegg has been supported by apparent evidence that children from poor families of high ability massively underachieve relative to children from wealthy families of similar ability, and that conversely children from wealthy families of low ability massively overachieve relative to children from poor families matched on ability. Below we see a figure that has been widely circulated in the media (from Feinstein, 2003). I will refer to this is Figure 2, following Feinstein’s own labelling.
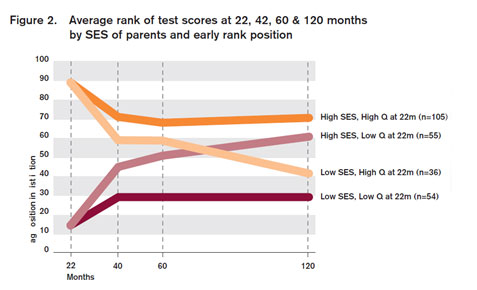
While I do not wish to comment on the proposals themselves, I suggest that this Figure illustrates a a statistical artifact called “regression toward the mean,” and that the apparently shocking pattern of results is simply what we would expect when we have two populations of differing ability, and several imperfect measurements of that ability.
Regression toward the mean (abbreviated from now on as RTTM) occurs whenever measurements are selected for their extremeness (e.g., the high or low scores are chosen for further analysis), and then compared to other measurements of the same quantity. In this example, we select students that score high or low on a test at one time, and then compare those scores to ones taken at another time. The second measure can be taken before, after, or at the same time as the first. When this is done we will find that, on average, the extreme measurements that we selected will be accompanied by less extreme measurements at another time. This might seem mystical when stated like this, but if we think of everyday examples it is obviously true. For instance, imagine that you look at all the sprints made by Usain Bolt, and find his personal best. You then look at how fast he ran on his next sprint. It will probably be slightly slower, and his previous sprint will be slower as well. That is because we deliberately selected the fastest sprint and then looked at what happened on other sprints. If we had selected his slowest sprint, we would find the same thing reversed – the adjacent sprints would now be a bit faster.
We don’t just observe this for the most extreme events, but in general if we select an above or below average event then the adjacent events will tend to be more average. In an appendix I describe other ways we might observe RTTM in our everyday life. The list is chosen to show how we can easily misinterpret this statistical anomaly as having causal significance, and indeed how we probably do so every day.
To understand RTTM we have to break down an observation (such as a sprint or a dinner) into two parts. One part is the enduring ability of the sprinter, which is repeated trial after trial. The other part includes idiosyncratic factors which either speed up or slow down the sprinter on each occasion. For Usain, the track might be more or less slippery from sprint to sprint, there might be a tailwind or a headwind, or a variety of other factors. The very fast sprints are likely to have been bolstered by idiosyncratic factors that are less likely to be there on other sprints, while the very slow ones are likely to have been impeded by other non-repeating idiosyncratic factors.
The graph above turns on an interpretation of how a measure of ability changes over time. Any measure of ability can be broken into two components – the true score, which is the actual ability of the respondent – and the idiosyncratic component just described which is often called error. (This is a simplification, and interested readers are urged to read the superb article by Nesselroade et. al. referred to below). A very reliable test is one that produces results with little error, while the results from an unreliable one will have a lot of error.
In the original study, the ability of children was measured at several points. Their ability scores at one of those points (22 months, the first measurement) were ranked. The top and bottom quartile were then selected, and these were then divided into rich and poor (high and low SES). Figure 2 shows what happens to the relative performance of these children over time.
It is useful to take the analysis in two stages. First, lets look at the wealth groups taken individually. RTTM predicts that the low ability group will improve over time, while the high ability group will get worse. Moreover, this effect will occur almost entirely from the first measurement to the second. This is very clear in Figure 2, which shows big drops and leaps from 22 months and 40 months, and not a lot thereafter.
In brief, the ability of the high ability groups was overestimated at 22 months – simply because they were selected based on unreliable test scores – and the ability of the low ability groups was underestimated. This was corrected on later occasions when extreme positive and negative error was less likely to occur.
But there is another element in Figure 2. The rich/low ability group goes up more than the poor/low ability group, and the poor/high ability group goes down more than the rich/high ability group. In fact, at 10 years, both rich groups are outperforming both poor groups. This is the shocking element of Figure 2. It looks like the poor/high ability children are plummeting in ability, while the rich, even of low ability, are catching up and surpassing them. Can RTTM explain this?
The answer is yes. We expect that the mean toward which each group will regress is its own population mean. To illustrate, imagine that two extremely tall parents have a son and a daughter. We expect their children to be taller than average, but not as tall as their parents. Moreover, we will expect the daughter to be shorter than the son. The daughter will regress toward the mean height of females, and the son toward the mean height of males.
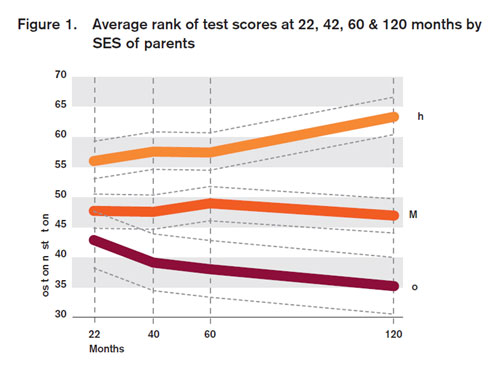
So if the rich group has a higher average ability than the poor group, we expect the mean toward which the extreme scores will regress to be higher. In fact, this is the case. In Figure 1 of Feinstein’s paper, we see that the average rank of the rich group is indeed higher at all ages. The data do not tell us why this is the case, and clearly this is an important if somewhat unsurprising observation, but because this is true we can predict that both rich groups will end up closer to their own population mean, and both poor groups farther from their mean. And this is what occurs[i].
The original article describing these results contains a further piece of evidence that regression to the mean is the primary cause of the effect. In Figure 3 it shows the measurements of children selected for extreme performance at 40 months. Regression toward the mean predicts that if we look backwards at their 22 month scores, and then forward to their 60 month scores, we will see regression effects in both directions. We do. If we did not recognise this as the effect of regression toward the mean we would draw some strange conclusions. At age 22 months some children suddenly improve very rapidly, with poor children improving more quickly than rich ones. But then just as suddenly, their performance falls off, with poor children falling more rapidly than rich ones. This is a pure statistical artifact, and has no causal significance whatsoever. As with Figure 2, the correct way to interpret the graph is by simply eliminating the 40 month measurement and looking at what is left. If we do that there is very little change in the four groups, which show nearly constant performance from 22 months to 120 months.
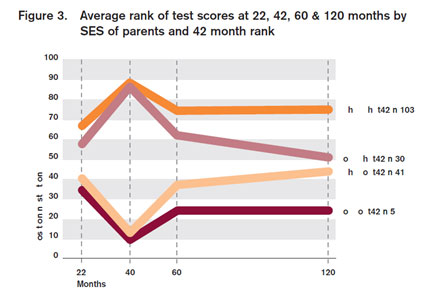
It is possible that RTTM is not the only time-linked effect in the data, and so I will put the most charitable interpretation on it. In both Figure 2 and Figure 3 we see that even after the first adjustment period (that is, from 22 to 40 months, or 40 to 60 months) the relative performance of the rich/low ability group goes up, and that of the poor/high ability group goes down. While this could easily be due to RTTM (again, the Nesselroade et al. article is a good source for understanding this) it may be that there is a genuine effect of environment, with (for example) rich children coming to outrank poor ones because of their enriched environment. It should be noted, however, that even if this is a genuine effect – and more analyses are needed– it is very small compared to the RTTM effect which is surely the major reason that Figure 2 was so widely published.
The data of Figure 2 have been put forward to support the policy of intervening in the environments of poor children, because their intellectual development or opportunities are being impaired by those environments. This is an admirable goal, and no doubt there is other evidence that can be brought to bear on the issue. But these data do not suggest that such a policy would work. What looks like the social scandal of poor children failing to live up to their potential, is a statistical artifact due to an inappropriate analysis of the data.
Other phenomena possibly due to regression toward the mean
Tall fathers tend to have sons that are slightly shorter than they are ... and tall sons tend to have fathers that are slightly shorter than they are.
An outstanding meal at a restaurant can bring us back on another occasion, when the meal is not so good as it was before. (Notice how we never go back to restaurants that disappointed us the first time, so we never experience regression in the opposite direction.)
An X-factor contestant who messes up one week, will probably come back the next week with a better performance. But one who performs outstandingly one week, is probably more ordinary the next.
A political party that wins by a landslide, wins by a smaller margin next time. A political party that is routed, makes a modest comeback next time.
The sophomore slump. An artist that produces an outstanding first album, comes back with one that is a bit of a disappointment. (Notice that only artists whose first album is exceptional get a second chance – this is the selection required for RTTM).
Child stars are usually less successful as adult stars. (But note that adult stars were probably less successful as child actors.)
Great books make average movies.
After speed cameras are installed in accident blackspots, the accident rate goes down.
Some technicalities
Regression toward the mean is synonymous with imperfect correlation. If the squared correlation coefficient between two measures is less than one, there will be RTTM such that on average, when one measurement deviates from the mean, the other measurement will be closer to the mean. Alternatively, if RTTM is observed, it means that the squared correlation coefficient is less than one. Recognising this makes the concept of RTTM less magical.
RTTM does not mean, however, that if you have an extreme measure that the other measure will always be closer to the mean. But rather, that if you select many measurements that deviate systematically from the mean (i.e., they are either higher or lower) then the average of the other measurements will be closer to the mean. It also does not mean that the two unselected sets of measurements differ in their mean and variance. They might or might not, it is irrelevant.
Imagine two sets of measurements, X1 and X2. Assume that the mean of all the measurements is the same, denote it m, as is the standard deviation. (If these assumptions are not met it is simple to adjust, but conceptually it adds nothing) The correlation between each set is denoted rij, as in r12 and so forth. Suppose we have a measure x1 drawn from the first set, and the corresponding measure x2 drawn from the second.
Then the expected value of x2 is:
E(x2) = m+ r12(x1-m).
And the expected value of x1 is
E(x1) = m+ r12(x2-m).
If the measurements are completely unreliable (r12 = 0) then E(x1) and E(x2) = m, while if they are completely reliable (r12 = 1) then E(x1) = E(x2) = x1 = x2.
And that is regression toward the mean.
References
The original work is reported in the following papers:
Feinstein, L. (2003). Very Early. CentrePiece, Summer, 24-30.
Feinstein, L. (1998) Pre-School educational inequality? British Children in the 1970 cohort. CEP discussion paper 404.
A more technical and comprehensive account of regression toward the mean is found in this classic article:
Nesselroade, J. R., Stigler, S.M., & Baltes, P. B. (1980). Regression toward the mean and the study of change. Psychological Bulletin, 88, 622-637.
[i] Note that the average rank of high SES groups goes up and the average rank of low SES groups goes down. This is what we would expect if there are differences between groups, but the early measures of ability contain more error than the later. The 22 month measures of cognitive ability are more unreliable than later ones, and therefore this accounts for much of the observed pattern.
