Statistical Inference
Statistics is an important component of much of the work within WIDER, some particular areas of relevant expertise in the statistics department are outlined below.
Missing data and intractable likelihood
For almost all real-life epidemics it is impossible to observe complete information about the way a disease has spread through a population. For example, it is usually impossible to recover the exact time an individual has been infected and from which individual the infection originated. If there isn’t a perfect or “gold-standard” diagnostic test available, it will not even be possible to determine whether an individual was infected or not with certainty. Unfortunately these “missing data” are needed to calculate the likelihood function, on which statistical inferences are usually based. One solution is to attempt to infer the missing data alongside the parameters of interest; however this greatly increases the scale and complexity of the inference problem.
A particular strength is the use of advanced MCMC techniques.
Outbreak detection
Sophisticated statistical models can be fitted to routinely collected data in an attempt to identify changes in behaviour, such as epidemics, case clusters or outbreaks. Once putative outbreaks have been identified they can be referred to public health services for further investigation. It is therefore extremely important that the rate of false alarms is kept as small as possible. If extra information is available, such as the spatial location of cases, then this can be used to improve the detection sensitivity. These methods are currently being applied in a public health setting to cases of campylobacteriosis in New Zealand. However it remains extremely challenging to process the large amount of information that is available rapidly enough to produce timely interventions.
InFER
The InFER project is developing the statistical techniques for performing inference of parameters for inprogress epidemics.
Coalescent models
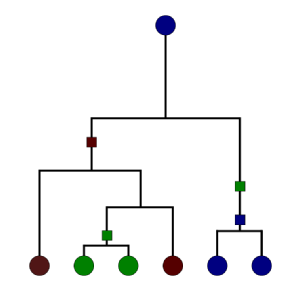
Coalescent models from population genetics can be used to infer the infection chain from genetic data sampled from the pathogen responsible for the disease. The behaviour of a population evolving according to forwards-in-time processes such as the Wright-Fisher and Moran models is described by the Kingman coalescent in the infinite-size population limit. Importantly, the Kingman coalescent allows a backwards-in-time interpretation of the process starting with just a sample from the population at a particular time and following the ancestral tree backwards to the common ancestor. Mutations (square boxes in the diagram) can be included. In our case the population is the set of infected individuals at the present time; the ancestral tree then gives the infection chain for a sample of these individuals. The Kingman approximation allows for easy computation of the likelihood of a given ancestral tree.
Another method of epidemic inference begins with a model describing the (stochastic) epidemic process and supposes that noisy data on the number of infectives in the population is available at certain time points throughout the process. Particle MCMC methods are used to estimate parameters associated with the process, such as rates of infection/under-reporting, by considering the likelihood of the observations for each given set of parameter values and updating the values accordingly. Incorporating information from the coalescent model analysis into this procedure allows us to construct a joint likelihood function for both observations and sequence samples, which improves the accuracy of the inference.
Funded by EPSRC, BBSRC, MRC
People involved
Gareth Roberts, FRS
Simon Spencer
Thomas House
Ashley Ford
Chris Pettitt
