In this project researchers are designing new self-tuning MCMC algorithms allowing for automated and reliable Bayesian inference.

Bayesian inference is often the preferred methodological approach for researchers in genomics, infectious diseases, climate, or financial and industrial models, because it quantifies uncertainty of the statistical reasoning through the posterior probability distributions of such quantities as the model parameters, the missing data, or the predictions. These posterior distributions are explored using MCMC algorithms, such as the Metropolis-Hastings, the Metropolis Adjusted Langevin algorithm, the Gibbs sampler, Hybrid Monte Carlo, or the slice sampler. However, in modern high-dimensional applications, of the shelf versions of these algorithms often need extensive tuning for optimised performance, that are time consuming and require expert knowledge.

Adaptive MCMC is an approach to design self-tuning MCMC algorithms that learn about the target distribution as the sampling progresses and optimise parameters of the sampling algorithm accordingly. They allow for automated and reliable Bayesian inference in these important applications.

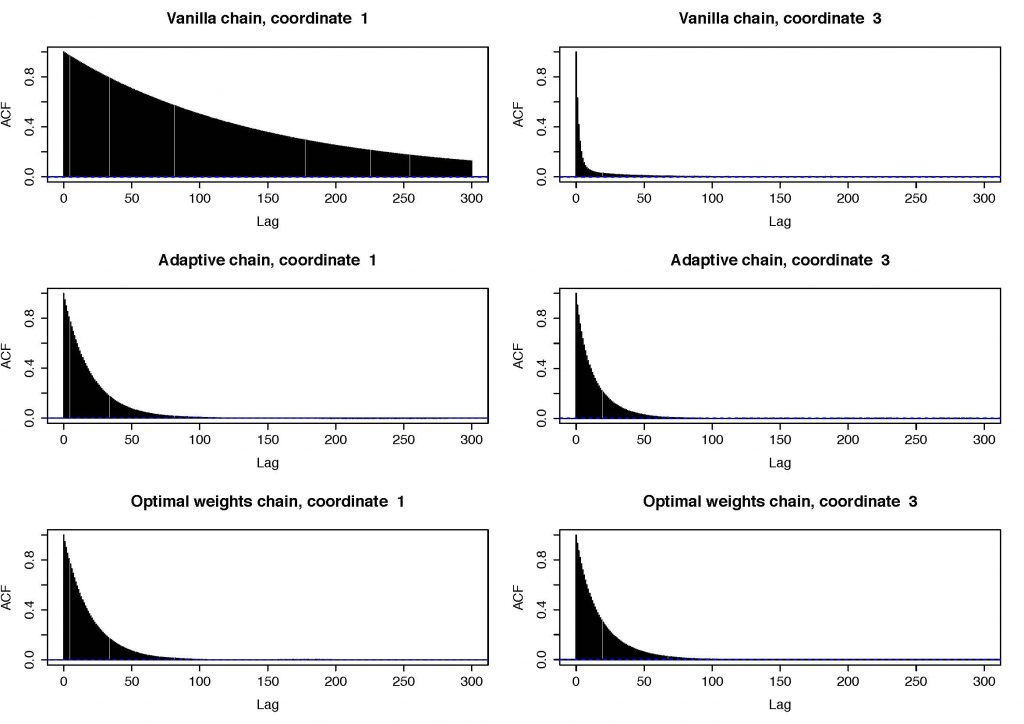
Autocorrelation plot of an adaptive Gibbs sampler

Organiser:

Dr Krys Latuszynski, Associate Professor of Statistics, University of Warwick

People:

Cyril Chimisov, University of Warwick

Chris Holmes, University of Oxford

Alex Mijatovic, King's College London

Emilia Pompe, University of Oxford

Gareth Roberts, University of Warwick

Mark Steel, University of Warwick

Lukasz Szpruch, University of Edinburgh

Wilfrid Kendall, University of Warwick

David Green, The Alan Turing Institute

External collaborators:

Louis Aslett, Durham University

Jim Griffin, University of Kent

Jeff Rosenthal, University of Toronto