Neutrinoless double beta decay (0νββ) is a very slow lepton-number-violating nuclear transition that occurs if neutrinos have mass (and oscillation experiments tell us they do), and are their own antiparticles, i.e. Majorana particles. An initial nucleus (Z,A), with proton number Z and total nucleon number A decays to (Z + 2,A) emitting two electrons in the process.

With the exception of one unconfirmed observation, 0νββ has never been seen, and searches are ongoing in a number of laboratories across the world. 0νββ-decay violates total lepton number by two units and is forbidden according to the Standard model. It can be seen as two subsequent steps (see Figures 1 and 2)

First a neutron decays under the emission of a right-handed νe . It is then absorbed as a left-handed νe . To fulfil these conditions, the neutrino must be a Majorana particle (the neutrino and antineutrino are identical). This is different from all other fermions where particles and antiparticles can be distinguished by their charge. Majorana particles are preferred by most Grand Unified Theories to explain the small magnitude of neutrino masses [1].

Double beta decay is considered the ”gold plated” channel to probe the fundamental character of neutrinos. In order for the neutrino to be able to change helicity, it is necessary that it is a massive particle. The reason is that the wavefunction describing neutrino mass eigenstates for mν > 0 has no fixed helicity and therefore, besides the dominant left-handed contribution, has an admixture of a right-handed component (or vice versa for antineutrinos), which is proportional to mν /E.

It is 0νββ-decay that offers the possibility to probe the nature and absolute mass of the neutrino. For the decay to occur at all, the neutrino must be a Majorana particle and if 0νββ exists, the absolute mass can be found.

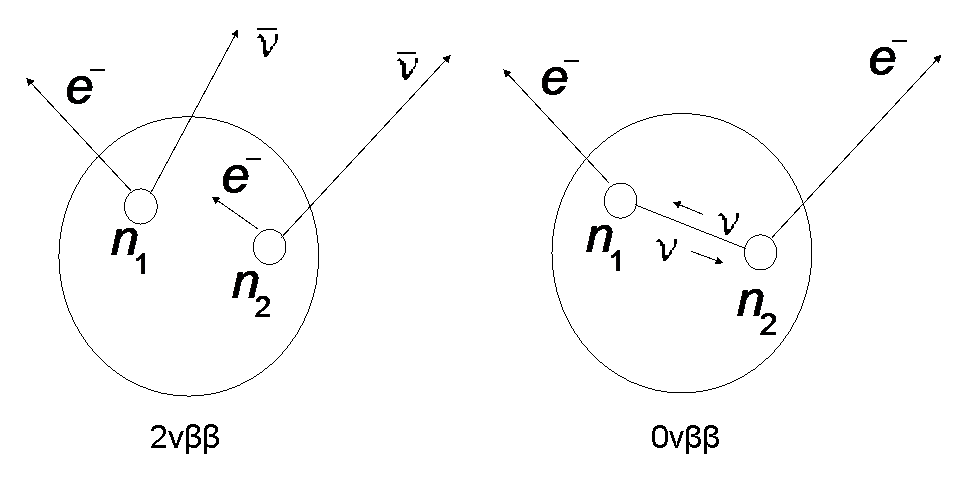
Figure 1: Principle of double beta decay. Left, the simultaneous decay of two neutrons as an allowed higher order process (2νββ-decay). Right, the lepton-number violating mode (0νββ-decay) where the neutrino only occurs as a virtual particle. This process is not allowed in the Standard Model [2], [1].

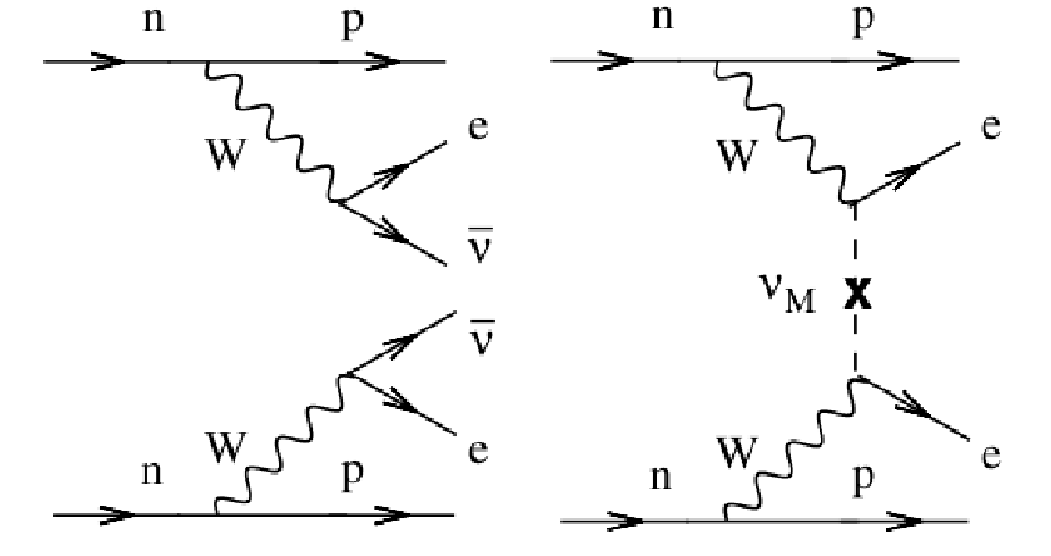
Figure 2: Feynman Diagrams for 2νββ (left) and 0νββ (right) [3].

References

[1] K. Zuber, Double Beta Decay, Contemp. Phys. 45 (2004) 491-502

[2] Kai Zuber, Neutrino Physics, Institute of Physics (2004)

[3] F.T. Avignone III et al., Double Beta Decay, Majorana Neutrinos, and Neutrino Mass, arxiv:0708.1033v2 [nucl-ex] (2007)