Inference methodology and numerical methods developed by Sbider

Inference of mechanistic models
Sbider develops new techniques for Bayesian inference for simulator-based and sequentially-structured models. These include novel Markov chain Monte Carlo, sequential Monte Carlo and approximate Bayesian computation methods.
Bayesian inference
In order to make accurate predictions using mathematical models, their parameters must be fit to existing data. Bayesian inference quantifies uncertainty about these parameters which can, in turn, lead to a description of uncertainty in predictions. Knowledge of this uncertainty leads to more robust decision-making based on models.
Improved MCMC
Markov chain Monte Carlo (MCMC) is a key technique for Bayesian inference of parameters, but can be computationally expensive, particularly when using a large data set. Researchers in Sbider have developed new MCMC approaches that do not use the standard Metropolis-Hastings approach, and offer improved scaling on large data sets.

Piecewise-deterministic Markov process (PDMPs)
The zig-zag sampler is a continuous-time process that simulates piecewise-deterministic trajectories that can be used for Monte Carlo estimation. Work in Sbider has focussed on automating the use of this approach in applications.

Bayesian evidence synthesis
Bayesian evidence synthesis helps to merge information coming from disparate sources. An open challenge is how to properly account for the noise generated by each process involved and the effect of the dependencies among said data sources.
Fusing information sources
Real-life models are often complex and include many layers on which we might have separate, noisy and often non-independent data. For example, if an epidemic spreads in a population we might have individual-level data on patients' histories, surveillance data on reported cases at different levels of care, expert knowledge on the virus development or health policies in place etcetera.
Individual-based models
For some applications it is more effective to model individuals rather than devising a model at the population level. For example, in an epidemic model we can view the infection status of each individual as a hidden Markov model. Since individuals can interact by infecting each other, then the population forms a coupled hidden Markov model. Inference in such models can be challenging, and necessitates the development of new methods.
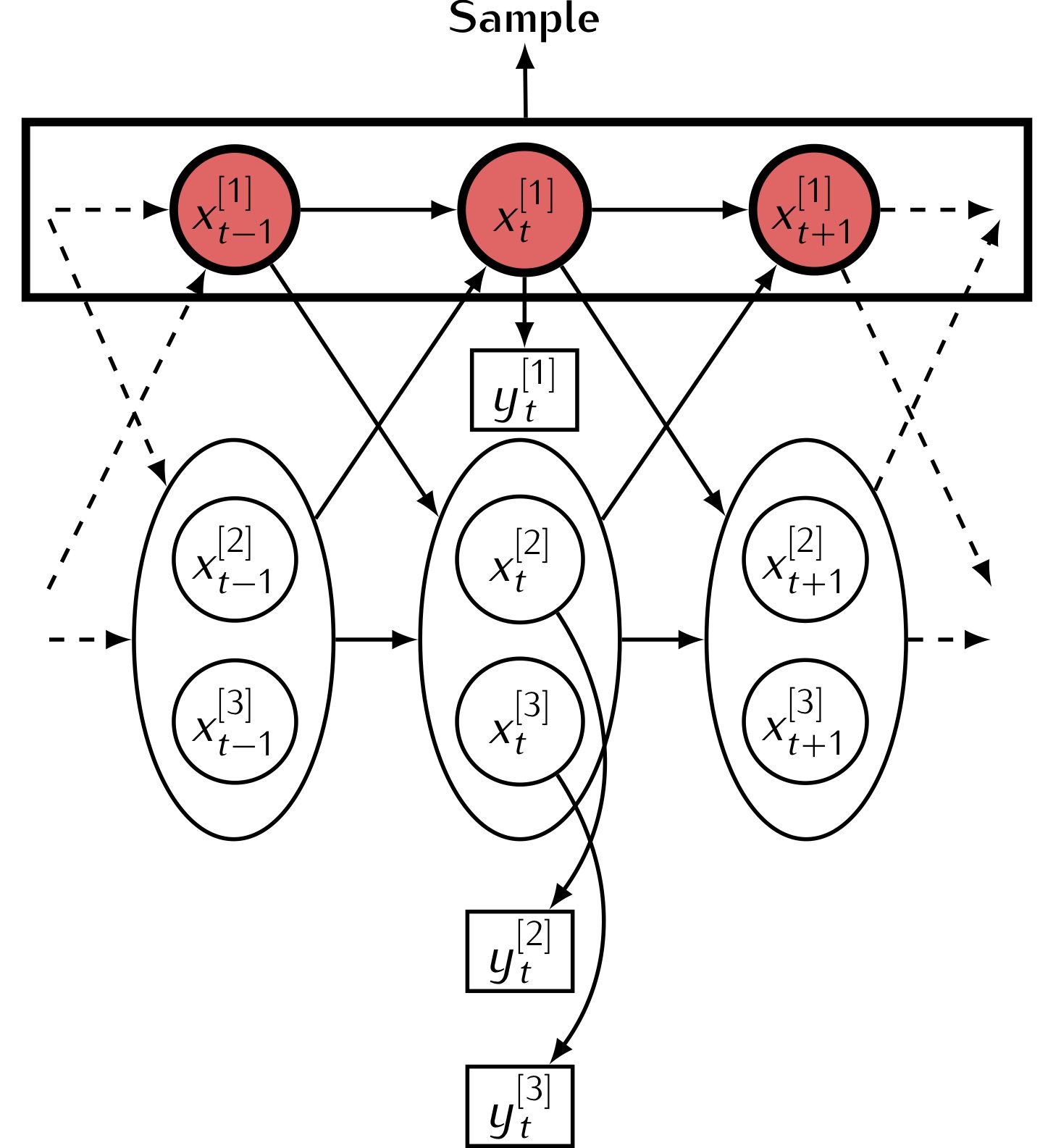
iFFBS
We have developed a novel algorithm for inferring the hidden infection status of each individual called the individual forward filtering backward sampling algorithm (iFFBS). A key feature of this algorithm is that the computation time scales *linearly* in the size of the population and so it can be applied to large populations.

Numerical continuation
Numerical continuation techniques for (systems of) ordinary and partial differential equations employ iterative algorithms that numerically construct steady state solutions for large parameter ranges from a single known solution.
Solving parameterized nonlinear equations
Numerical continuation allows researchers to numerically study unstable solutions which are often equally important as their stable counterparts, for example when transient dynamics occur in systems. It can also be used to determine solution properties, such as the stability of periodic travelling wave solutions in models for spatially patterned ecosystems.
Circadian rhythm and health
The network of molecular clocks within each cell regulates key physiological functions, such as sleep, metabolism, hormone secretion, and DNA repair, over a 24-hour cycle. Circadian disruption is linked to increased risk of chronic diseases, including cancer, cardiovascular disorders, and psychiatric conditions, and is associated with worse outcomes in cancer patients.

Detecting circadian disruption
Sbider experts develop the statistical methodology and results needed for circadian biomarker data and their use for detecting circadian disruption.
