In collaboration with the Department of Medical Physics & Clinical Engineering, University of Sheffield and Department of Mechanical Engineering, University of Bath.

1. Background/Context

The focus for the present work was to investigate the potential for mathematical modelling to improve the support for clinical decision making in critical care environments, specifically the adult general intensive care unit (ICU). Two very different strands of internationally recognised research work came together at the start of this project: the development of real-time data management systems for ICUs1,2 (Department of Medical Physics and Clinical Engineering, Sheffield) and the development of compartmental models of the respiratory system3,4 (Department of Mechanical Engineering, University of Bath).

Critical care environments (CCEs) describe those clinical areas where the functionality of organ systems are artificially maintained or supported. Examples of critical care environments include ICUs, operating theatres (as a result of anaesthesia) and trauma units. Such environments are data intensive with up to 40 measurements an hour being recorded by nursing staff in the ICU1,2. In addition to these measurements, there are the results from chemical and biochemical assays together with images (particularly chest x-rays) that provide information on the chemical and anatomical components of disease. These complex, multidimensional data sets are used to inform decisions by clinical staff on patient management1.

Using computer technology to routinely support clinical decision making remains an unachieved goal. We believe one of the reasons for this is that pattern recognition approaches (for example using neural networks or production systems) cannot be made sufficiently patient specific. Our hypothesis is that mathematical models of (patho-) physiological processes can inherently be made more patient specific and therefore offer the potential for supporting the clinical decision making processes. The data intensive nature of critical care environments provide an ideal opportunity for developing mathematical models of the respiratory system. This project has developed and validated a mathematical model of the respiratory system of artificially ventilated adult patients on an ICU

2. Key Advances and Supporting Methodology

2.1 Introduction & Overview

The starting point for modelling within this project was a model of the respiratory system developed by the Bath group for assessing the breathing apparatus used by deep sea divers3,4. This model was essentially a pneumatic model. In a series of meetings between the two collaborating research groups, this model was reviewed to determine work needed to port this model to artificially ventilated patients. A number of key differences existed:

• Artificially ventilated patients on the ICU make minimal respiratory effort and the respiratory rate and tidal volume are primarily determined by the ventilator settings. There is no control of respiration.
• During artificial ventilation, the patient’s upper airway is bypassed by an endotracheal (ET) tube which is passed through the mouth and connects the patient to the ventilator.
• Patients considered within this study are admitted to the ICU as a result of acute lung disease resulting in inadequate blood oxygenation. Within the original Bathfp model the lung was simply a piston.
• The ventilator must be modelled

In order to create a comprehensive model of artificially ventilated patients, all these issues had to be addressed. In addition, a major problem with the previous Bathfp model of respiration was that it contained a large number of constants that could not be readily determined experimentally. Therefore a way of determining or eliminating these became an essential aim of the project if it were to yield a model which could be made patient specific. A block diagram of the model implemented is shown in figure 1. The Bathfp software was used for the implementation of the compartmental components of the model.

To implement this model, work has been undertaken in the following specific areas:

• Modelling the ventilator
• Modelling airflow within the ET tube and the major airways
• Modelling gas exchange in acute lung disease

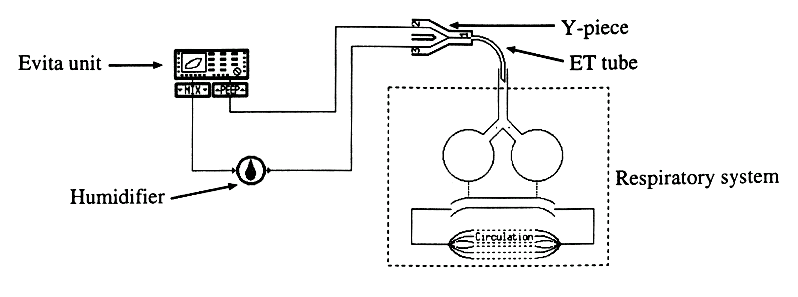
Figure 1: schematic diagram of the model of the respiratory system showing the Evita ventilator, the ET tube which connecting the ventilator to the patient's airways together with the lungs and pulmonary vascular circulation.

2.2 Modelling the Ventilator

In order to implement a model of an artificially ventilated patient, we needed to create a model of the standard ventilator used on the ICU at the Royal Hallamshire Hospital, Sheffield – the Draeger Evita II. The complete breathing circuit is shown in figure 1. On inspiration, gas is delivered to the patient through a mixer valve which is individually calibrated to deliver the required flow rate. On expiration, gas from the patient passes through a PEEP/PIP (Positive End Expiratory Pressure/Peak Inspiratory Pressure) valve which controls pressure within the airways. Whilst the Evita II has a number of different modes of operation, within this project we were only concerned with the Biphasic Positive Airways Pressure mode (BIPAP). In this, the clinician has control over the pressure applied during inspiration (Pinsp), the PEEP pressure, the time taken for the pressure to rise from PEEP to Pinsp; the ratio between inspiratory and expiratory times (Ti:Te) and the respiratory rate (RR). Gas flow is controlled to maintain the required pressure within the airways. Modelling of the pneumatic components of the ventilator is achieved by assuming uniform gas characteristics within a series of discrete vessels. Each vessel connects to at least one other vessel by ports where flow between vessels is controlled by a model of a pneumatic orifice. A friction model is used to account for the convoluted nature of the hoses which connect the ventilator to the ET tube. The simulation integrates the rate of change of pressure and temperature of the gas in each component together with the mass of gasses. Volumetric flow is determined from the ideal gas laws. Good agreement was found when the waveforms obtained from the model ventilator were compared with those obtained from the actual ventilator when the patient was replaced by a series of pneumatic resistances.

2.3 Modelling airflow within the ET tube and major airways

In the original Bathfp respiratory models the mouth and major airways were rigid smooth bodies where the dynamics of flow were described by ODEs. The introduction of the ET tube into the upper airways gives a discontinuity in tube diameters. In addition, the upper airways is not a smooth tube, but rather a tube with a series of semi-rigid rings around it. Peak flow from the ventilator is 60l/min giving Reynolds numbers of around 11,000 in the ET tube and 2,500 in the airways. Therefore flow will be turbulent and a 3D finite volume solution was implemented. From the literature, an ‘ideal’ geometry for the airways was identified and a finite volume model of this with an ET tube inserted into it implemented using CFX from AEA Technology. Figure 2 shows a typical result showing flow down the airways. Two options existed for incorporating the results from the 3D analysis into a compartmental model based around Bathfp: firstly to perform the 3D analysis for each time step within the compartmental model so that flow was calculated for a particular set of conditions; or secondly, to use a look up table where the flow was purely determined by pressure difference. An analysis of the transient characteristics of the flow following a step change in pressure difference across the model for different time steps in the 3D analysis showed that for the time steps used in the compartmental model, a look up table could be used. This video clip requires Windows Media Player, available at http://www.microsoft.com/windows/windowsmedia/download/

Figure 2 - velocity in the z direction determined by the 3D model of the ET tube and the airways. Blue is the low velocity whilst red is the high velocity. Click to animate.

2.4 Modelling gas exchange for acute lung disease

The primary reason most patients are admitted onto the adult general ICU is that they are suffering from acute lung disease resulting in an inability to maintain adequate blood oxygenation. Thus a method of modelling acute lung disease was an important element of the modelling process. It is well established in the literature that distribution of ventilation and perfusion over the lung is not homogenous5-8. Results from multiple inert gas elimination techniques (MIGET) suggest that for normal healthy lungs, ventilation and perfusion are log-normally distributed6,7 while patients with Adult Respiratory Distress Syndrome (ARDS)5 or other pathologies8 have been shown to have bimodal distributions. Using these results as a starting point, we examined a theoretical model of a multi-compartment lung having a log-normal distribution of VQ ratios to determine what pattern of damage would give rise to a bimodal distribution. This showed that a bimodal distribution for D% lung damage was obtained by setting the VQ ratios for a randomly selected D/100 compartments to 1% of their non-damaged value.

To validate our theoretical model we required a technique which spatially measures VQ ratios. Isotope (VQ) lung scans where different isotope compounds are used to assess ventilation (V) and lung perfusion (Q) independently are routinely used to investigate patients with suspected pulmonary embolism (PE). Such scans are however, not tomographic. Four views are normally taken: anterior, posterior, left oblique and right oblique. The problem with the two oblique views is that left and right lung images are partially superimposed – therefore only the anterior and posterior views were used in this study. Using data from the Visible Human project, a 3d anatomical model of the lungs within the thorax was constructed. Each voxel within this model was identified as belonging to 1 of 3 material types: lung, air and soft tissue. Using the linear attenuation coefficients for gamma radiation, this model was used to construct virtual VQ lung scans. These were very similar to lung scans obtained from normal subjects. Scans from 10 normal subjects and 10 subjects with PE were used to validate the theoretical model of lung damage. From the average of the anterior and posterior scans from each of these subjects the distribution of VQ values was obtained. To assess the degree of lung damage, these lung scans were first registered to the theoretical lung scans obtained from the Visible Human using an affine transform. Cross sectional slices from the Visible Human model could then have lung damage added, as shown in Figure 3. Ca and Cp are the measured isotope counts; t1 and t2, l1 and l2, and d1 and d2 represent the boundaries of the thorax, lung and damage respectively along a line in the anterior-posterior direction. Solving the integral equations relating Ca and Cp to isotope activity within the lung for d1 and d2 across the whole slice gives the size of the damaged area. Repeating this process across all slices allows us to compute a % damage by volume. 

This work was carried out in parallel with the development of the overall model and its evaluation is independent of the evaluation of the model as a whole. The key findings from this initial assessment of the model are:

• The distribution of VQ values from the isotope scans failed to show a bimodal distribution in subjects with PE.

• The modal values of the isotope VQ scans are approximately equal to the modal values in the theoretical VQ distributions

• The spread of model values in the VQ distributions from the isotope studies for subjects with PE was greater than that in normal subjects.

• The mean rms error between the isotope determined and distribution for the for the subjects with PE was independent of % damage (r2 = 0.16)

MIGET depends on gas transport across the alveolar membrane whereas the isotope technique used in this study is independent of the transport properties of the membrane which may account for the lack of a bimodal distribution. However, the other 3 results suggest that we may have a way of modelling acute lung damage. There is a need for further theoretical and experimental work to further investigate these findings.

2.5 Implementation and validation of complete model

Figure 1 shows the complete model of the respiratory system. The lung is modelled as a Windkessel model where the inflation volume is proportional to the integral of the applied pressure. The chest wall is modelled as a large surface area, small displacement piston. Gas transport across the alveolar membrane was calculated using previously published equations4. The experimental protocol involved making respiratory, cardiovascular and blood gas measurements before and then 15 minutes after a change in a single ventilator setting. Up to 3 changes in one of the following ventilator setting were made on each patient: Pinsp, PEEP, FiO2, Ti:Te. Patients were studied on the adult intensive care unit at the Royal Hallamshire Hosptial in Sheffield where a standard sedation regime is used. To investgate the effect changes in ventilator setting will have on the cardiovascular system, measurements (heart rate, systemic blood pressure, pulmonary artery pressure and central venous pressure) before and after changes in ventilator setting were compared using a chi-squared test. A Bonferroni correction was used to correct for multiple measurements. This showed no significant systematic change in these parameters with changes in ventilator setting. Therefore, it can be concluded that the sedation regime used abolished cardiac and respiratory interaction. Therefore, the pulmonary circulation was modelled as a constant flow rate ‘pipe’ with pre-set values of venous oxygen concentration (i.e. the metabolic demands are not modelled). Using this model, 46 changes in ventilator setting taken from 6 patients were analysed. The compliance of the lung for each set of measurement was obtained from the measured value of mouth pressure and the calculated value of lung volume (obtained by integrating the airflow signal) averaged over at least 10 breaths. The compliance values obtained from different measurements made on the same patient were very similar. Therefore, the mean value of compliance calculated over all the measurements taken from each patient were used to characterise the compliance for that patient. One of the constants within the model is the % lung damage. Unfortunately there is no direct method of determining this. Therefore, the degree (%) of lung damage for both O2 and CO2 for each set of measurements was determined using the 'gas exchange model'. The total ventilation was determined from the tidal volume (determined as described above) and the respiratory rate. There was a reasonable consistency in the % lung damage values obtained for O2 within the data from a single patient. This was not true for the CO2 values where there were very different values within each patient. Therefore, the mean % lung damage for O2 was used to characterise the lung damage for each patient.

For each set of data an analysis was run. The ventilator settings, FiO2 venous blood gas values, and pulmonary perfusion were entered. The analysis was run for 120s of data irrespective of the respiratory rate. Preliminary studies showed that the results are settled to within 1% by this time. Once the analysis was complete, the arterial blood gas values, tidal volume and change in pressure at the distal end of the ET tube were extracted and a 'line of best fit' analysis was carried out on each of the parameters analysed (Table 1). The equation of the line provides an indication of how the relationship deviated from the line of identity whilst r2 shows how much of the variance in the data is described by the correlation between the measured and modelled parameters.

2.6 Conclusions

The current models are derived from physiological principles and currently have not been optimised in any way. Therefore the most important test currently is that the correlations are linear with a high r2 factor. Differences in absolute values can be resolved by optimising constants.

The modelled mouth pressure is consistently higher than the measured mouth pressure suggesting that we have not correctly modelled the output port from the ventilator. Specifically, it is possible that flow is impaired by a high lung compliance. Since the lung is a Windkessel model, the increased mouth pressure also goes some way to account for higher modelled tidal volume when compared with the measured values. Within the model we have assumed a single value for lung compliance across a complete respiratory cycle which is not true. This probably accounts for the greater spread in tidal volume values than those observed in the mouth pressure. The correlation for PaCO2 values is better than that for O2 values. This may be due to the shallow slope of the O2 saturation curve for normal PaO2 values where large differences in PaO2 only give a small change in Oxygen saturation. The current analysis is slightly 'circular' as the same information goes into determining the % lung damage as goes into the final model. However, there is currently no independent way of quantifying lung damage.

The research has been successful in demonstrating that a modular approach to modelling physiological systems incorporating a number of different modelling methodologies gives a flexible model which shows good correlations with real data without optimisation. Through this, the understanding of how to model physiological systems had advanced. The modular approach allows a systematic approach to studying the relative sensitivities within the overall model. This, together with our novel approach to modelling lung disease and our finding that the model predicts different patterns of lung damage for O2 and CO2 requires further research.

3. Research Impact and Benefits to Society

The original stimulus for this work was clinical decision support in the ICU. The work carried out in this project provide a foundation to move towards that goal. Such a system would be valuable within the ICU, particularly to junior doctors. We have already had an approach from the Royal College of Paediatricians about the potential of using the model as a ‘simulator’ for teaching artificial ventilation of newborn babies. Much modelling in the past has been based on normal or ‘ideal’ physiological processes. In this project we specifically address the problem of modelling pathologies. Our exploitation plans include publication in journals from a number of different disciplines which should promote further collaborative work on modelling in medicine.

4. Further Research or Dissemination Activities

Currently 2 conference presentations have resulted from this work:

Murphy CM, Brook BD, Tilley DG, Miles AW, Breen D, Wilson AJ The validation of computer models of a mechanical ventilator and the human respiratory system intended for use in adult intensive care. In proceedings IMACS Symposium on Mathematical Modelling, February 2-4, 2000, Vienna University of Technology, Austria. ARGESIM Report No. 15. Volume 1. ISBN 3-901608-15-X. pp. 251-254. 2000

Brook BS, Murphy CM, Breen D, Miles AW, Tilley DG, Wilson AJ Mathematical modelling of the human respiratory system: quantification of lung injury in adult intensive care. 8th Oxford Conference: Frontiers in control and modelling of respiration, Cape Cod, Massachusetts. 2000.

5. References

[1] Wilson A.J, Bowes CL Holland J. Telematics and Protocols of Care in Critical Care Environments. In: Health Telematics for Clinical Guidelines and Protocols. Ed. Gordon C & Christiansen J., pub: IOP Press, Amsterdam 1994

[2] Ireland RH, James HV, Howes M, Wilson AJ. Design of a Summary Screen for an ICU Patient Data Management System. Med & Bio Eng & Comput. 35:397-403, 1997

[3] Tomlinson SP, Lo JK, Tilley DG. Time Transient Gas Exchange in the Respiratory System. IEEE Engineering in Medicine and Biology 12:64-70, 1973

[4] Tomlinson SP, Lo JK, Tilley DG. Computer Simulation of human interaction with underwater breathing equipment Proc Instn Mech Engrs Part H 208:249-261, 1994.

[5] Dantzsker DR, Brook CJ, Dehart P, Lynch JP, Weg JG. Ventilation-perfusion distributions in the adult respiratory distress syndrome. American Review of Respiratory Disease, 120:1039-1052, 1979

[6] Lenfant CL, Okubo T. Distribution function of pulmonary blood flow and ventilation-perfusion ratio in man. Journal of Applied Physiology, 24:668-677, 1968

[7] Wagner PD, Laravuso RB, Uhl RR, West JB. Continuous distributions of ventilation-perfusion ratios in normal subjects breathing air and 100% O2. Journal of Clinical Investigation, 54:54-68, 1974

[8] West JB, Wagner PD. Lung biology in health and disease. In: Bioengineering Aspects of the Lung, Volume 3, Pulmonary Gas Exchange. Ed. West JB Pub. Marcel Dekker, Inc, 1977