Additional thesis material
Self-contained Mathematica notebook
The Mandelbrot Monodromy
Below shows the interchanging of A and B pieces as we traverse a loop around the Mandelbrot set.
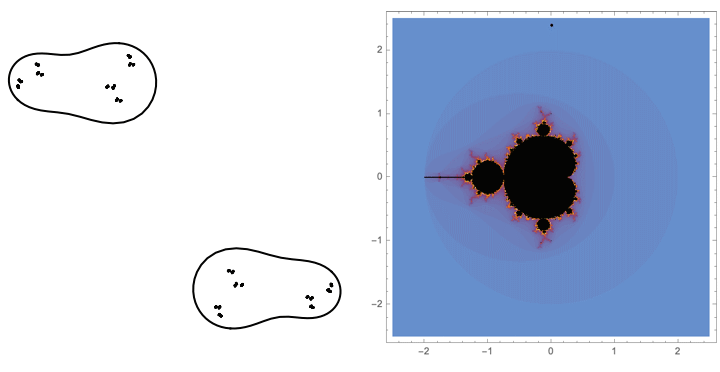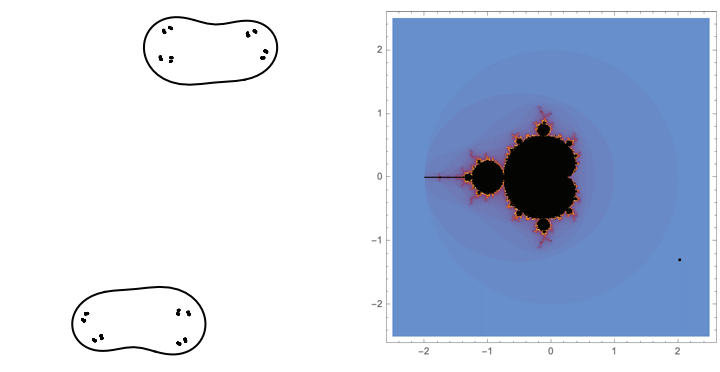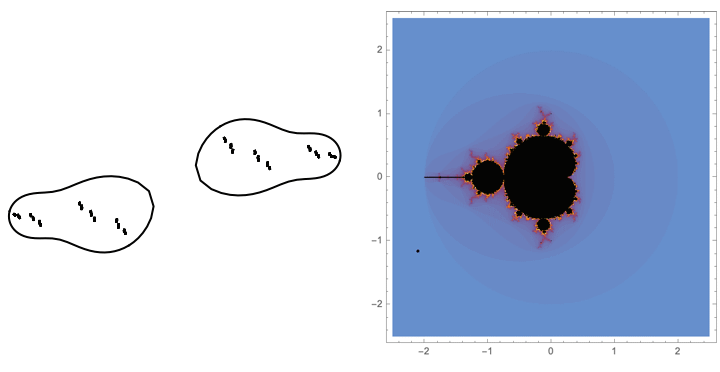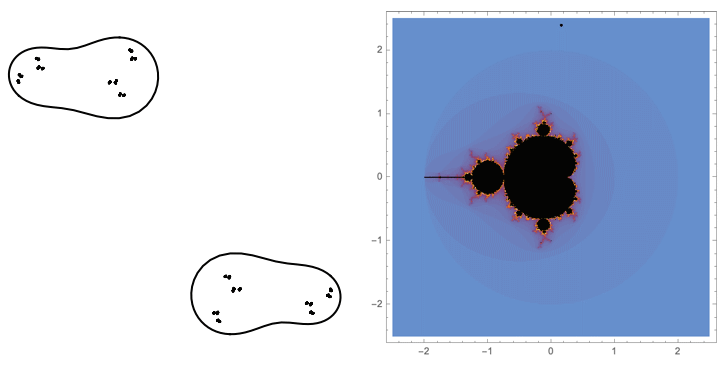
$B\star BAA$
The first loop in Hénon parameter space that we consider is Lipa's $B\star BAA$ loop in the $b=0.05i$ slice of parameter space.

Traversing this loop we see some "trapeze artists" being interchanged on the lower branch of our dynamical picture. These components have itinerary $B \star BAA$ under our map where the top branch is the $A$ branch and the bottom branch is the $B$ branch.
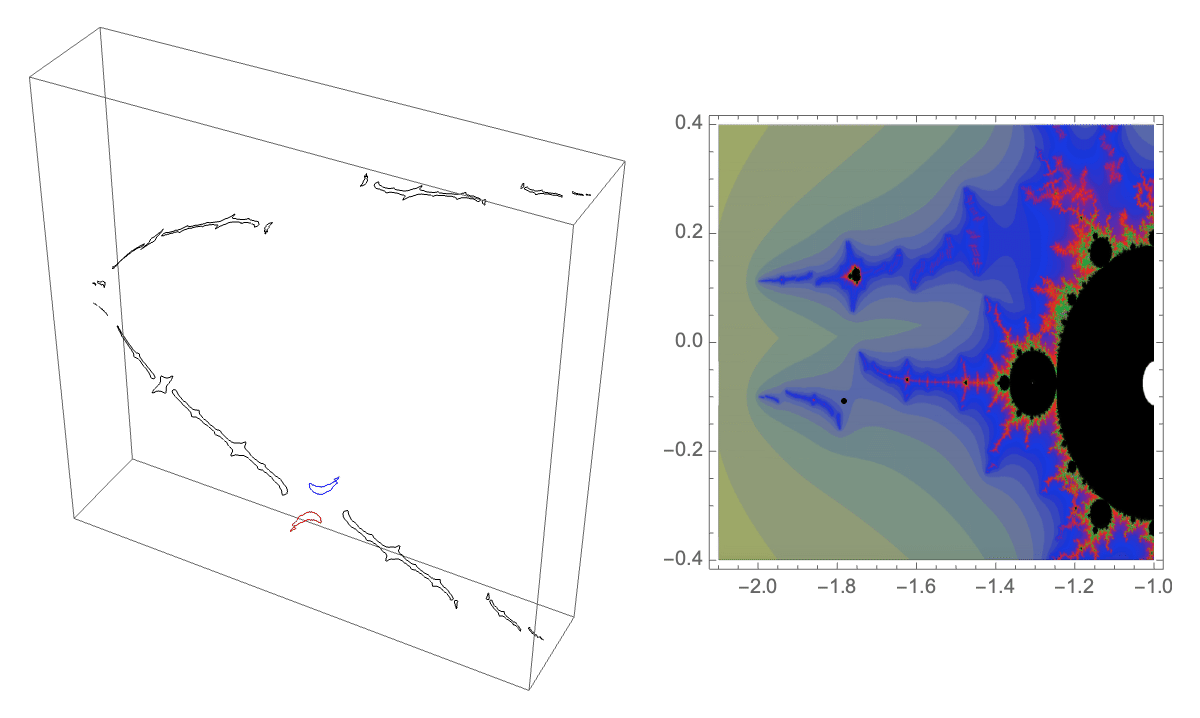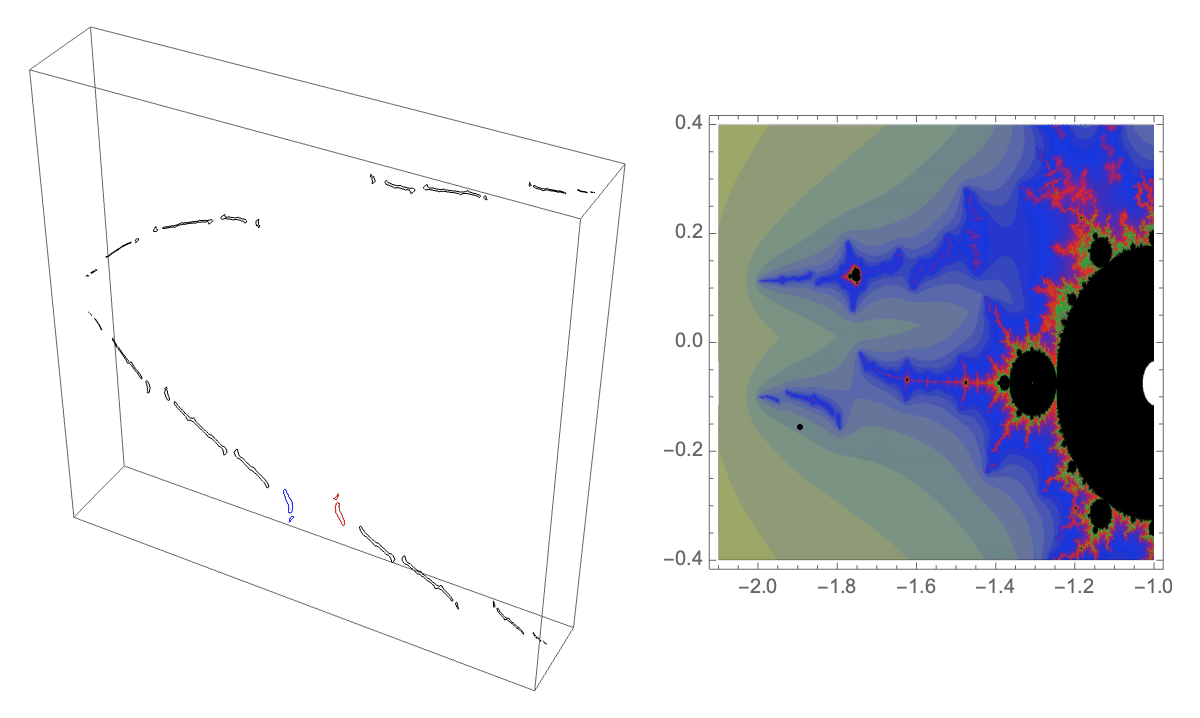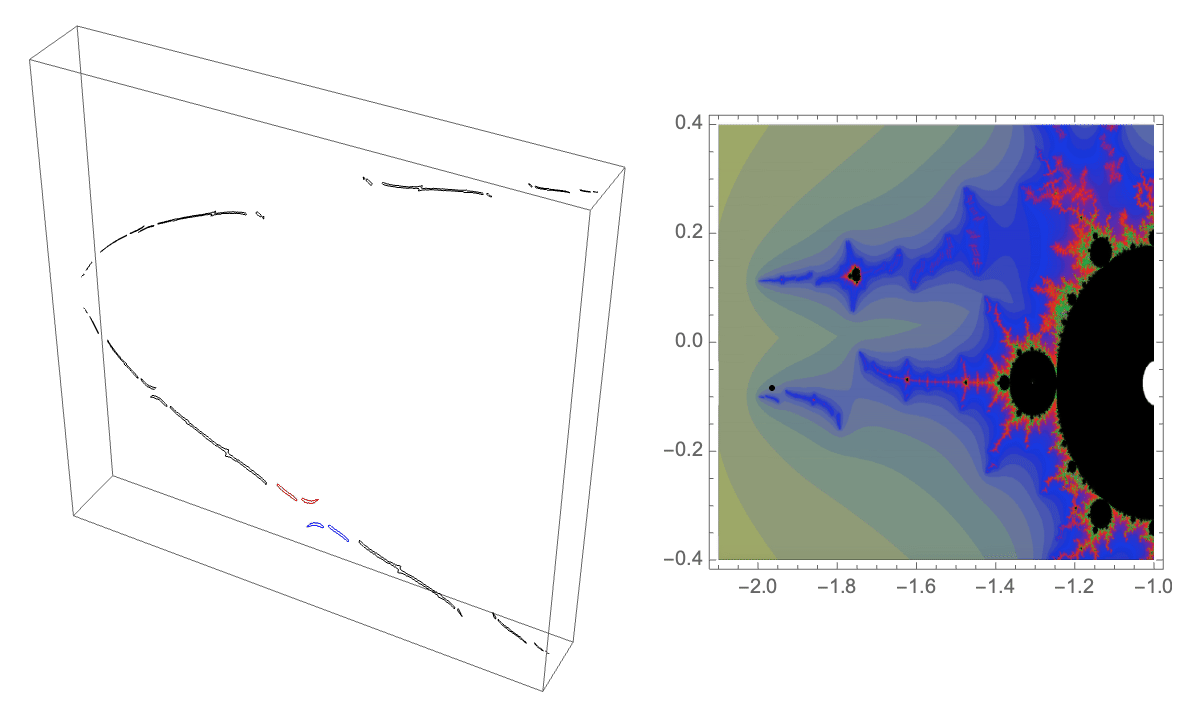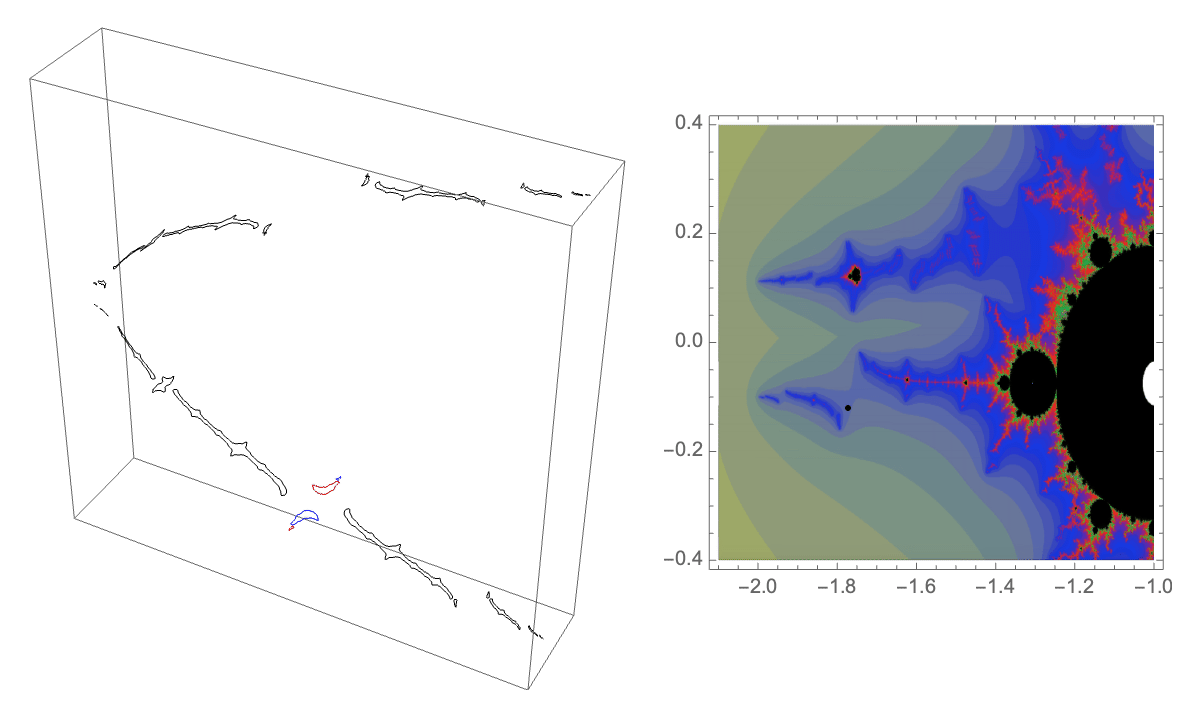
The corresponding external ray picture is given below. The orbit portrait consists of the rays with angles $\{1/7, 2/7, 3/7, 4/7, 5/7, 6/7\}$. The characteristic arc, defining the wake in parameter space in which this portrait is satisfied, is $\{3/7,4/7\}$. Adding the rays $\{3/14, 11/14\}$ gives the puzzle pieces. Pulling back the puzzle piece containing the critical point we can find a piece whose itinerary is $B \star BAA$. It is bound be rays of angles $\{5/14, 11/28, 17/28, 9/14\}$, shown in red below.
We see a critical value spinning as in the work of Blanchard, Devaney, and Keen. In this picture, we fix a dynamical picture and show a critical value of $gg^{\circ 2}$ between the trapeze artists. Following this critical point along the loop continuously we can look at its image under $gg^{\circ 2}$, giving the critical value. Considering all of the critical value as we traverse the loop we see they surround some components of the Julia set, i.e. as we move through the loop, the critical value spins around the component. This gives rise to the interchanging of the trapeze artists. Consider the external ray passing through this critical value.

Pulling it back gives some rays passing through the critical point and separating the trapeze artists, shown below. The piece either side of the critical ray maps with degree one to the component surrounded by our critical value loop. A branch cut argument explains why, as we traverse the loop, the trapeze artists are interchanges.

The $B\star BAA$ automorphism should also arising in the $b=-0.05i$ slice according to Lipa. In this slice, the herds break up in the opposite direction to those in the $b=0.05i$ slice. The parameter space picture below shows the $b=-0.05i$ slice and the corresponding loop we take.

The Julia set approximation as we traverse this loop is shown below. The only difference we see is that the components move clockwise as opposed to anticlockwise previously. This is because we traverse the loop clockwise here instead of anticlockwise, as before.
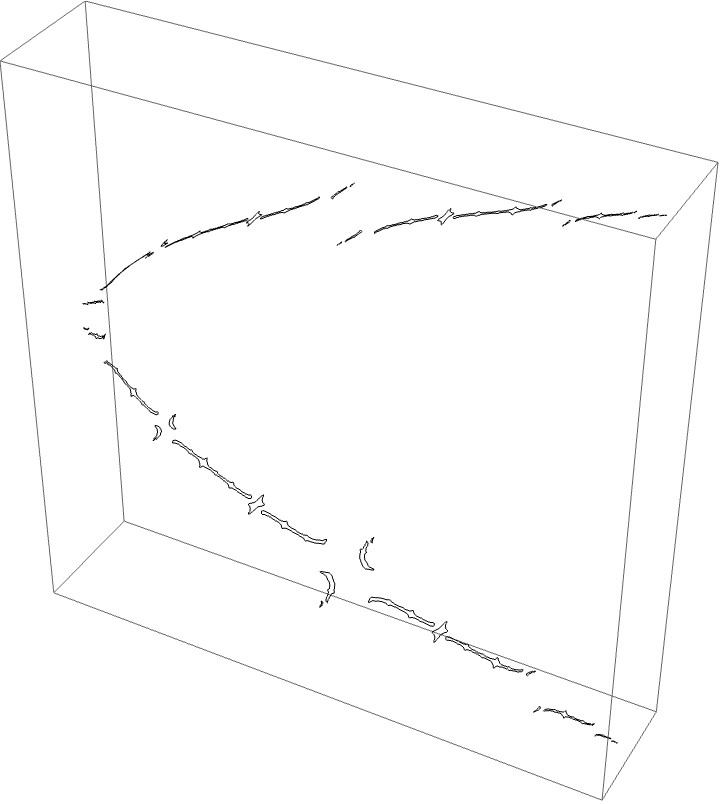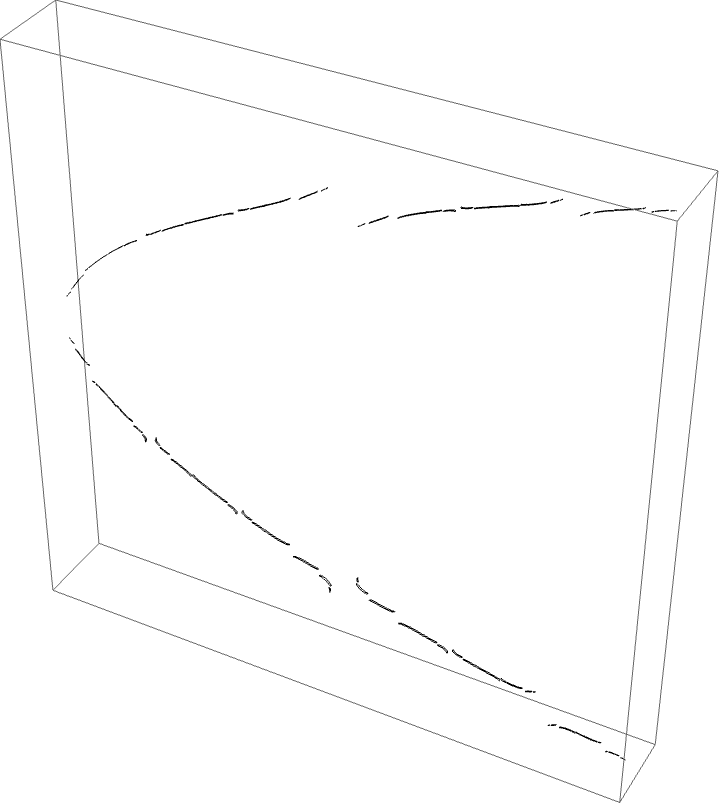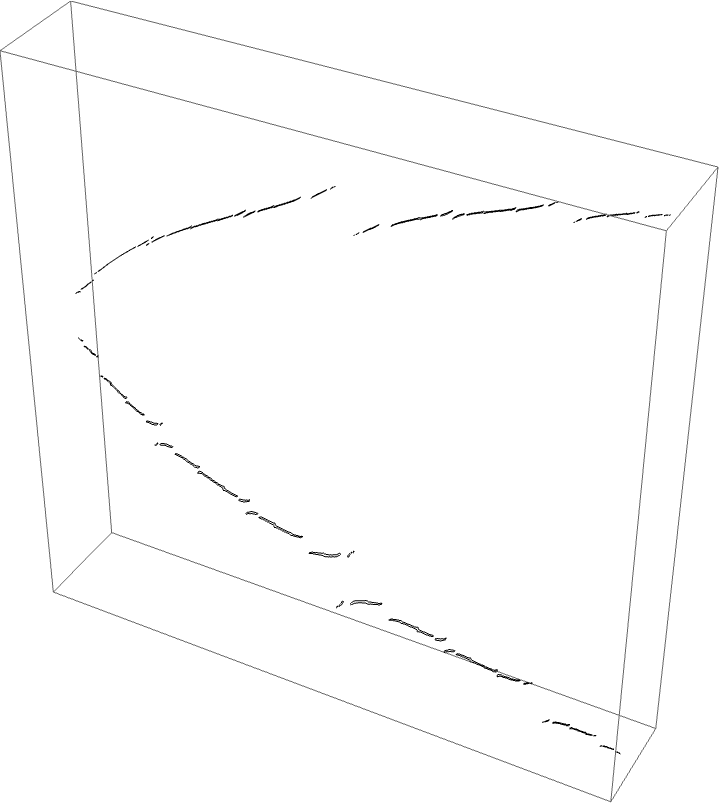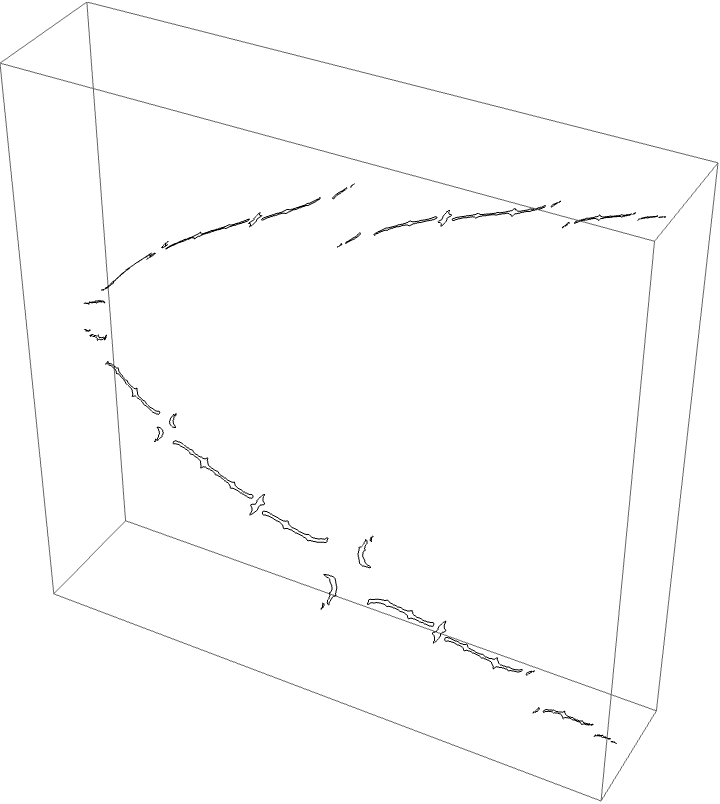
The A herd for the BABB wake, with the airplane wake conspicuous.
This wake is interesting since we have two orbit portraits which partition our dynamical space. The two marker strings are $A\star BAA$ and $A\star BABBA$. The puzzle pieces for the BABB wake are bound by rays $\{5/31, 9/31, 10/31, 11/31, 13/31, 18/31, 20/31, 21/31, 22/31, 26/31,13/26, 49/62\}$. The airplane puzzle pieces are as before. The puzzle piece with itinerary $A \star BAA$ is bound by rays $\{3/28, 1/7, 6/7, 25/28\}$, and the $A \star BABBA$ piece is bound by rays of angles $\{13/124, 9/62, 53/62, 111/124\}$.

Traversing this loop we see the below picture.
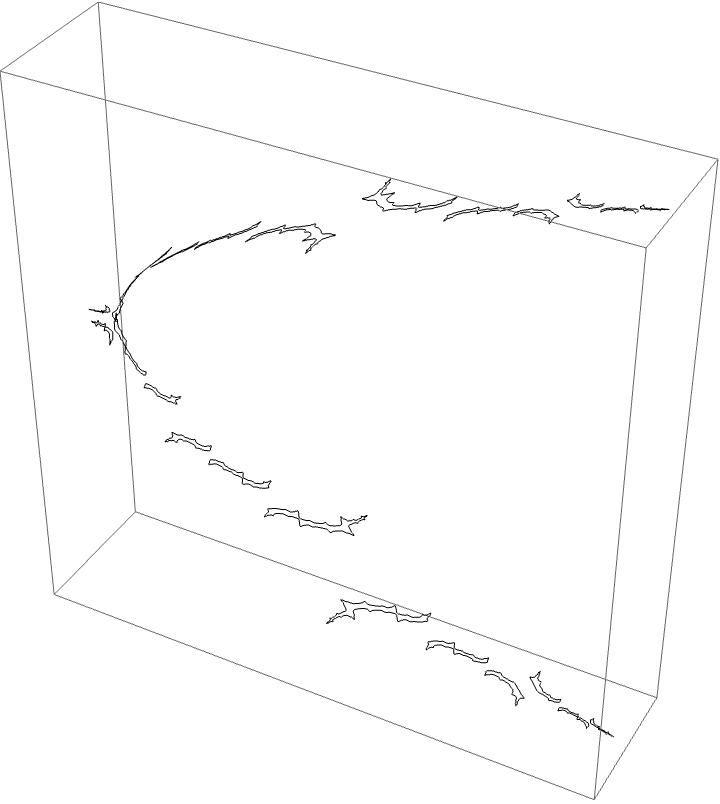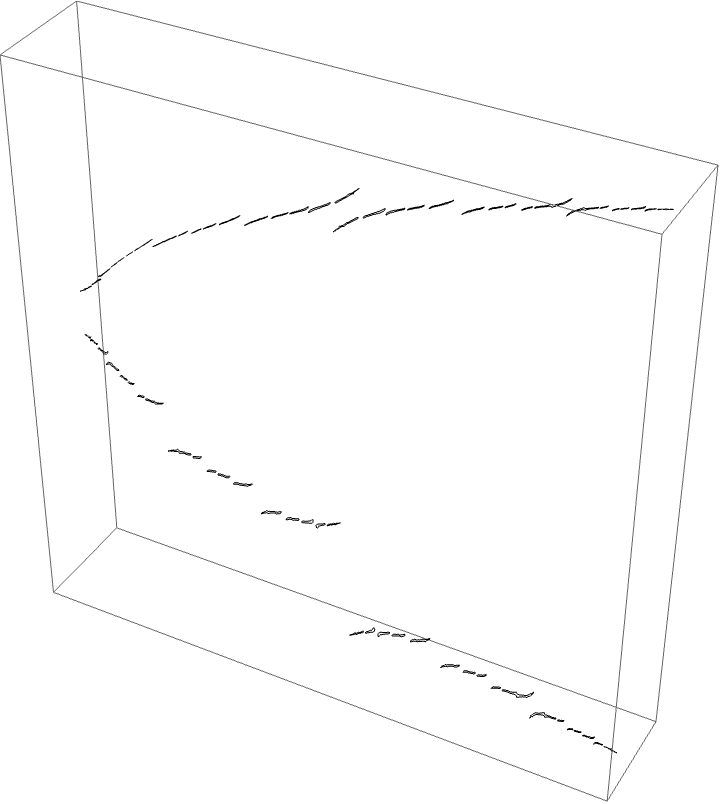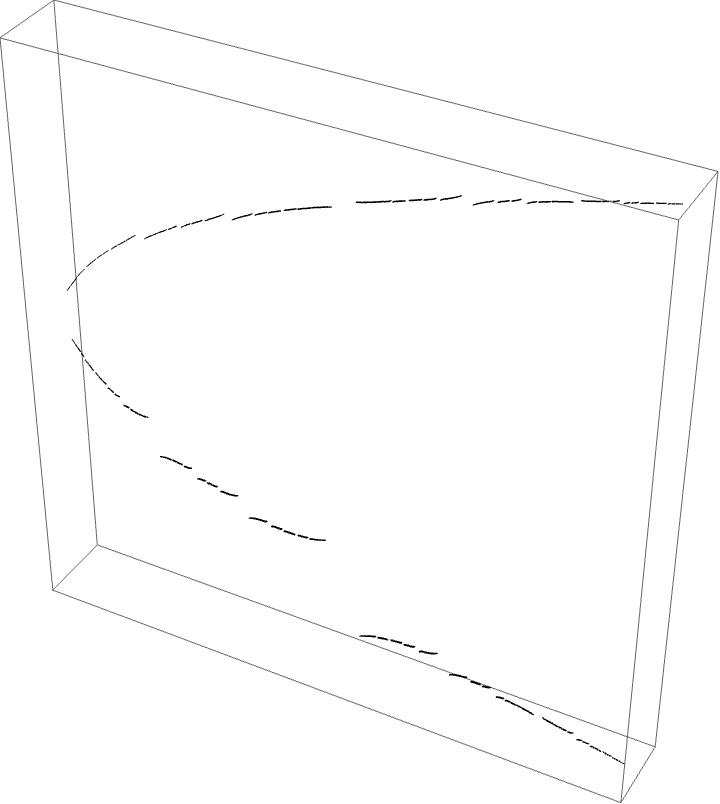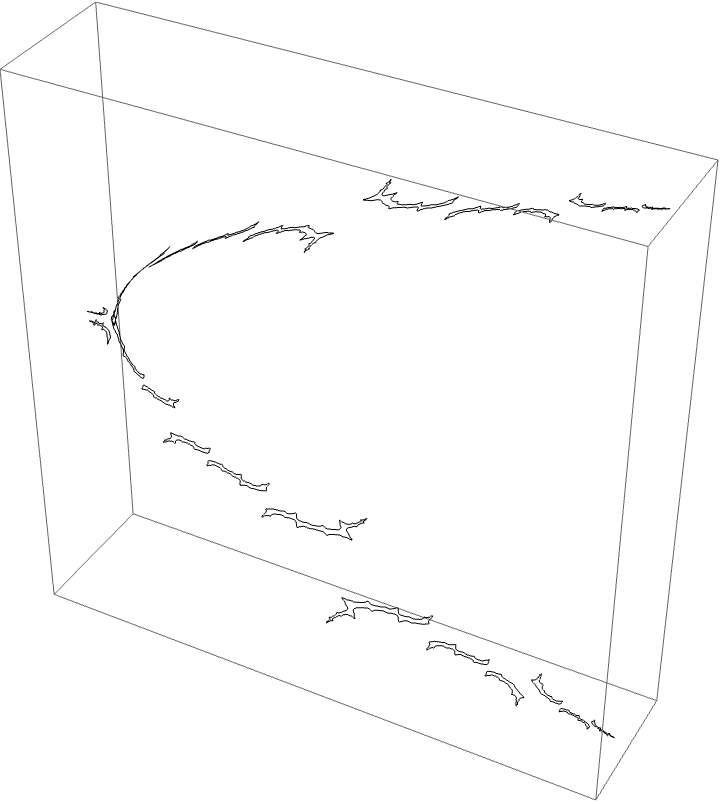
Since the airplane wake is conspicuous to the BABB wake we know the characteristic arc of the airplane portrait is contained in the characteristic arc of the BABB wake. This means the areas where monodromy occurs are nested. We can see this with the external ray picture. The $A \star BAA$ and $A \star BABBA$ are nested in the centre of the top branch of the picture, shown in red and magenta below.
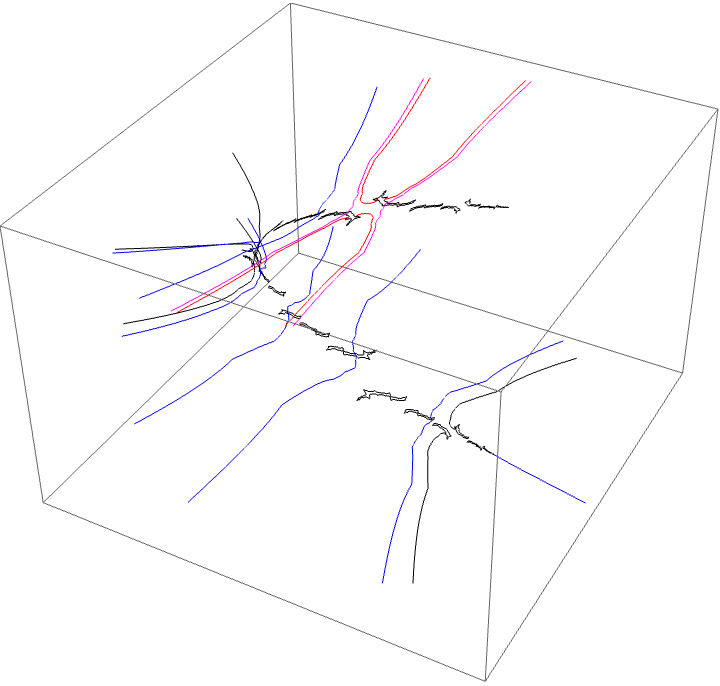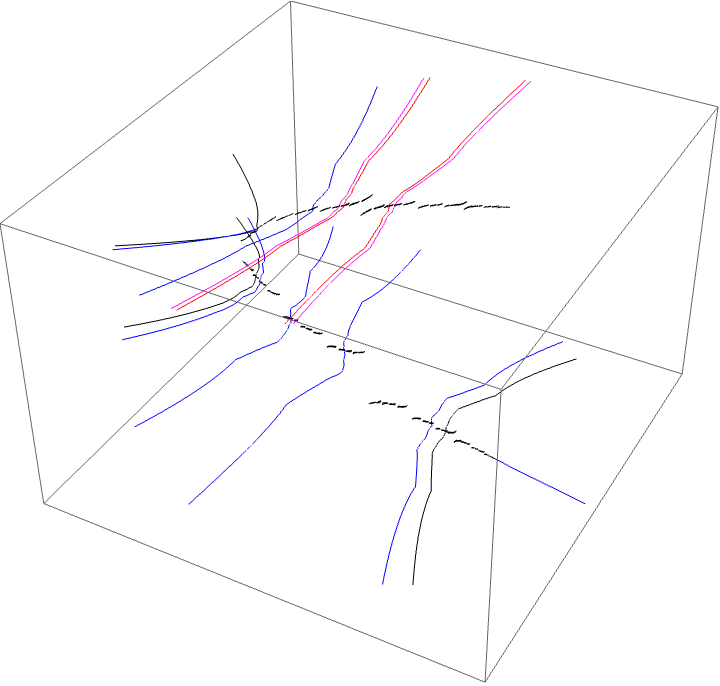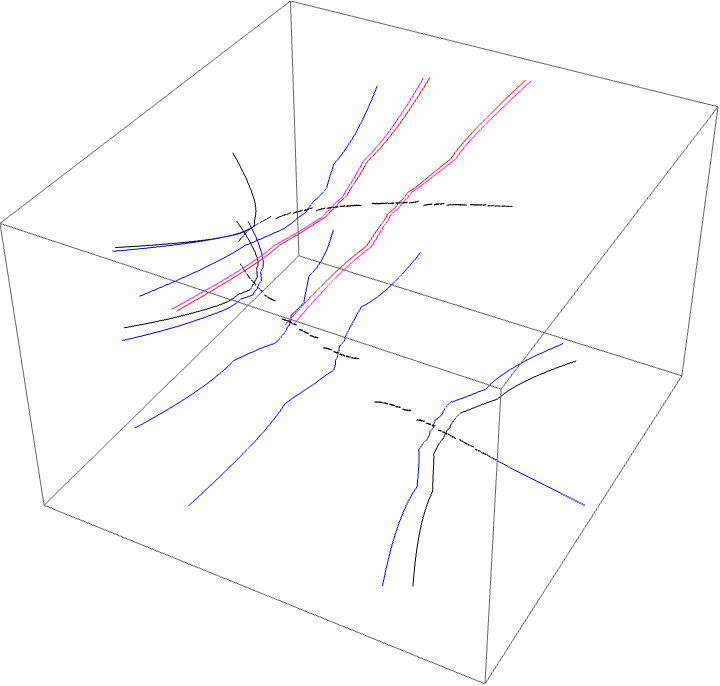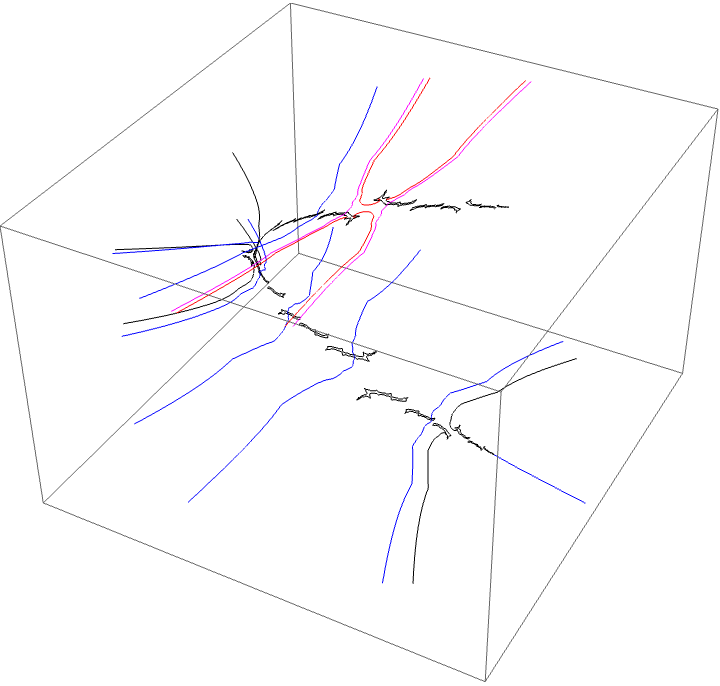
We see the following looping of the critical value. This is a critical value of $gg^{\circ 2}$. The critical point is in the centre of the trapeze artists.

A critical value of $gg^{\circ 3}$ gives rise to the same loop.
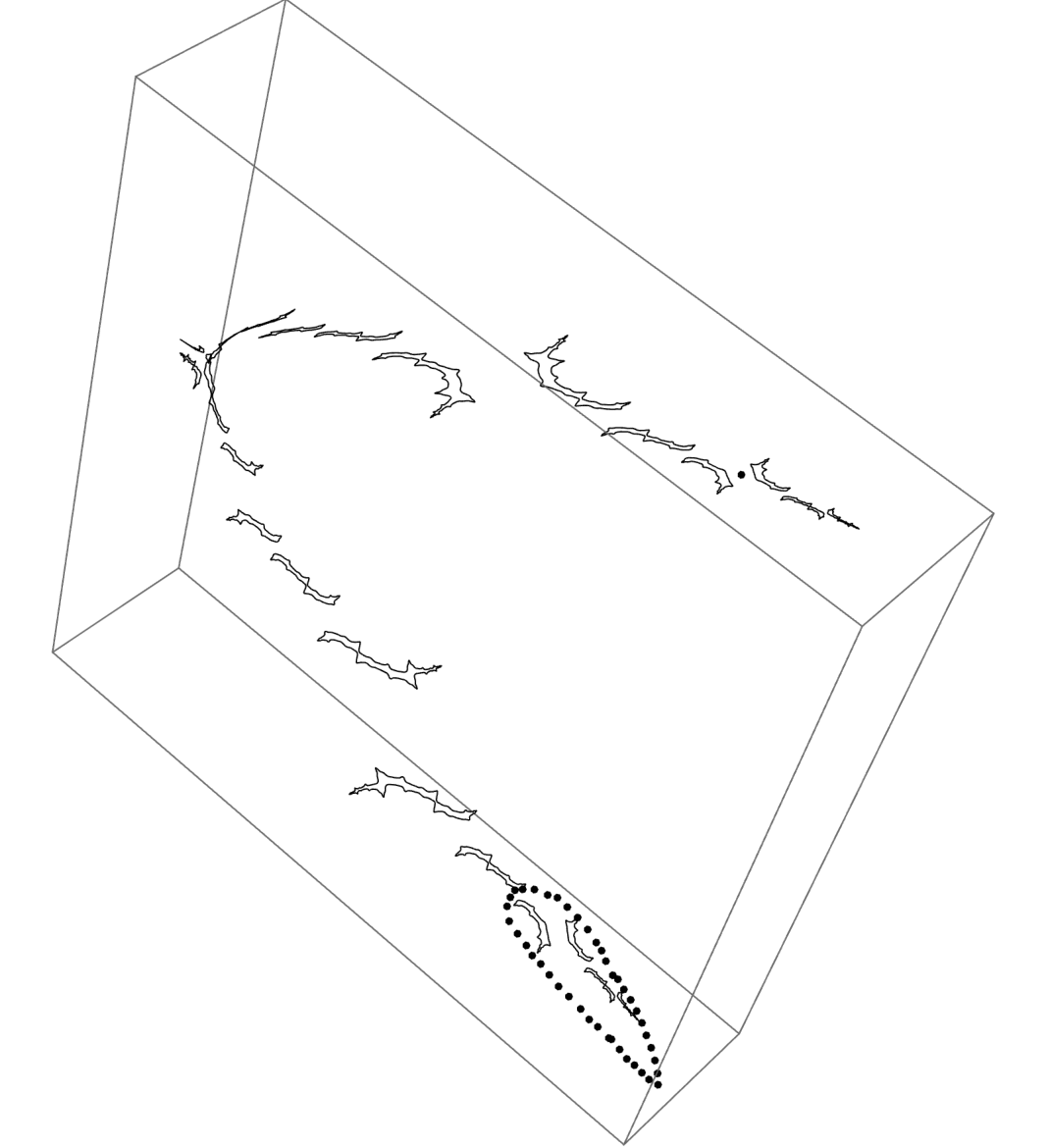
A second splitting of the airplane B herds
If we perturb out Jacobian parameter further we see out B herd splits into two herds coded by strings of length two.
Traversing a loop around the BB herd, and mapping our slice picture forward twice

we get the following dynamical picture
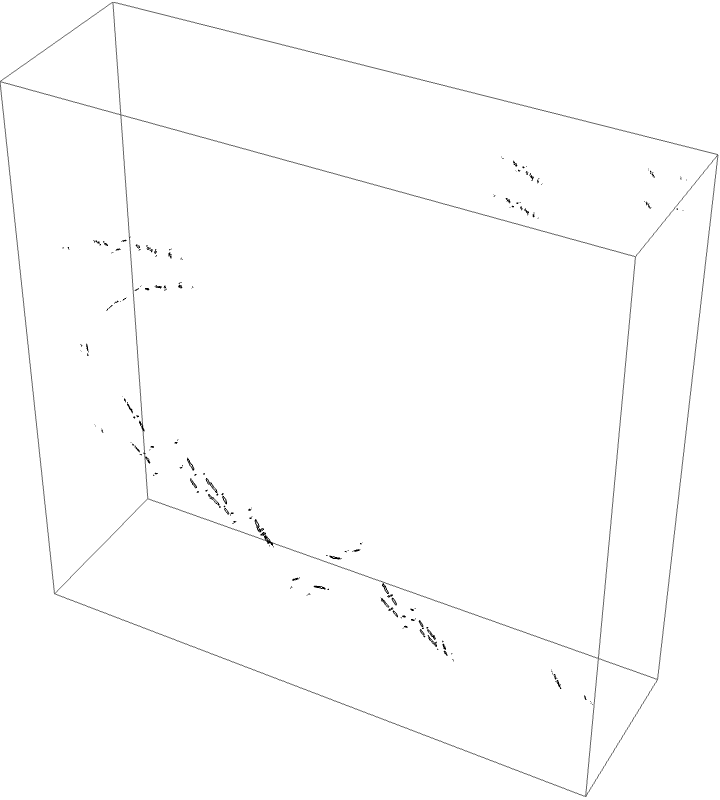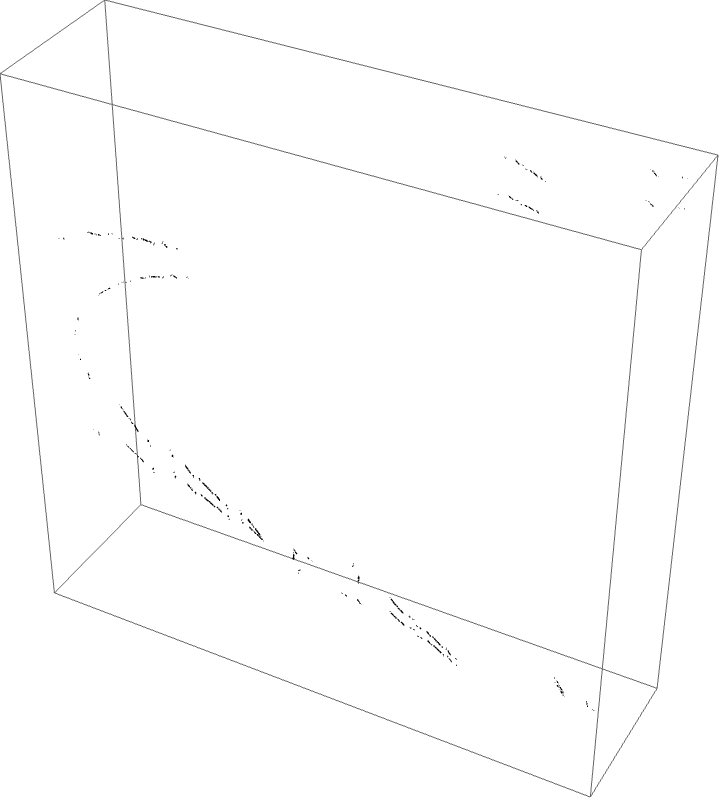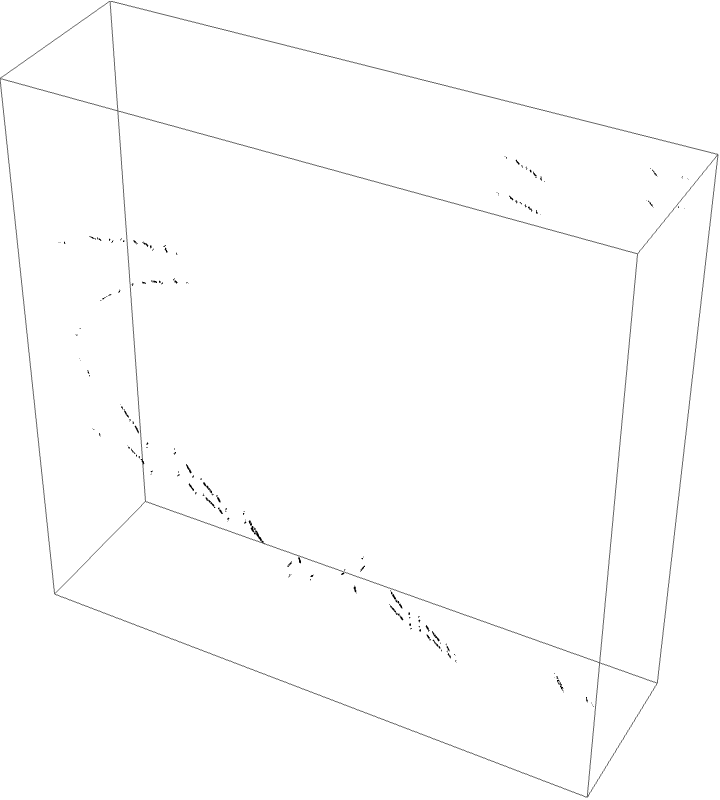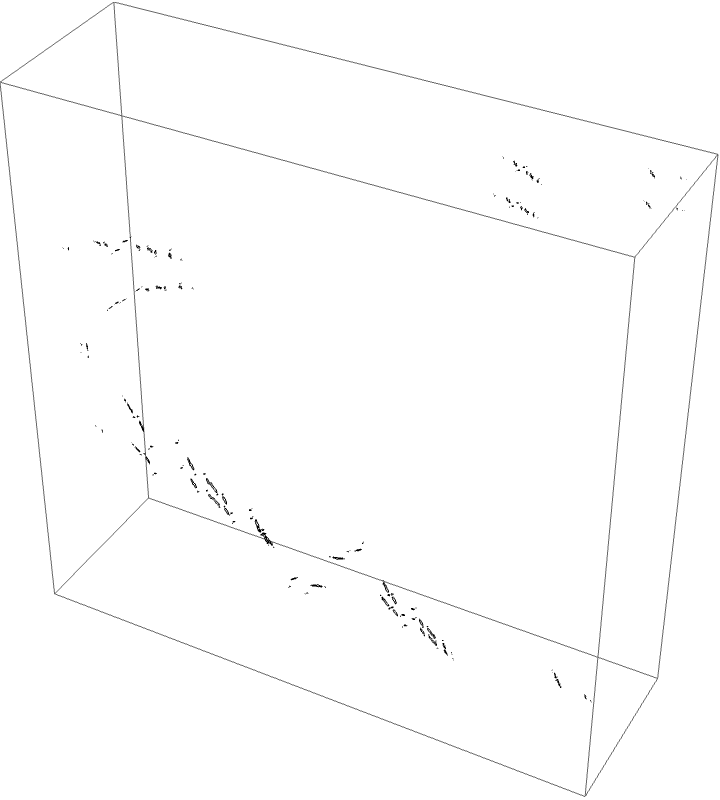
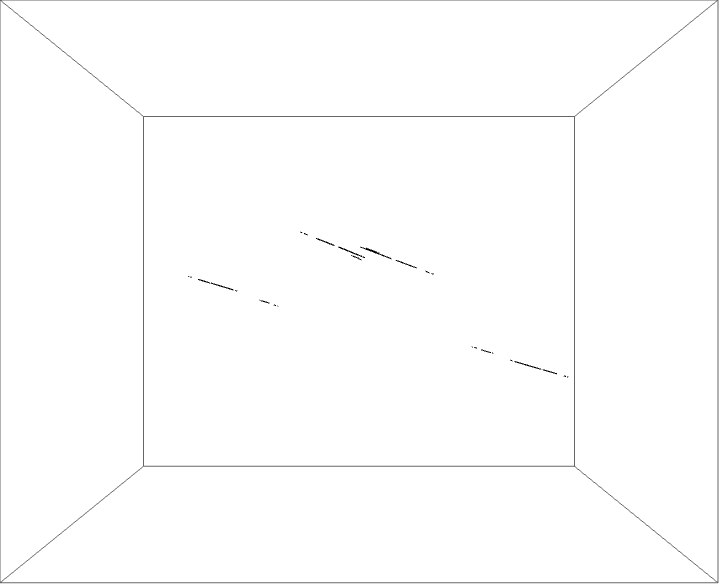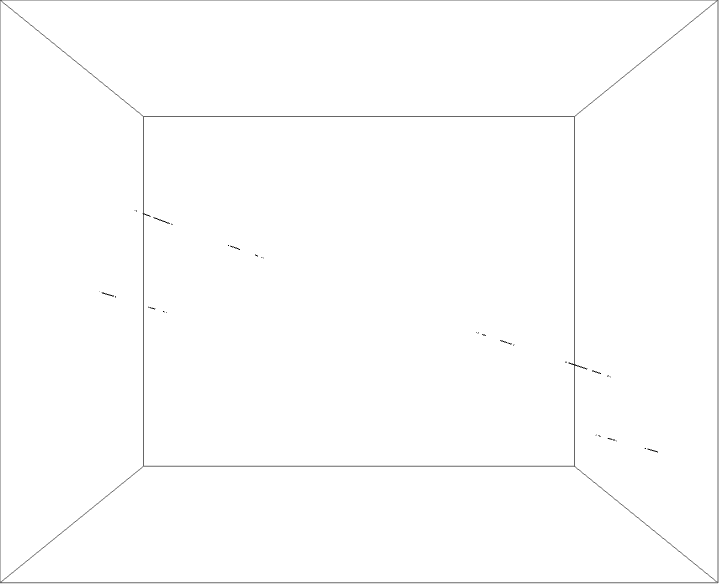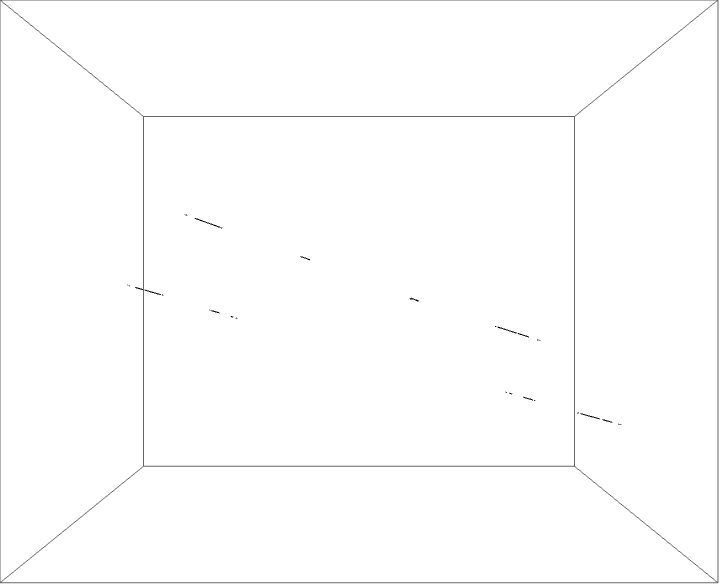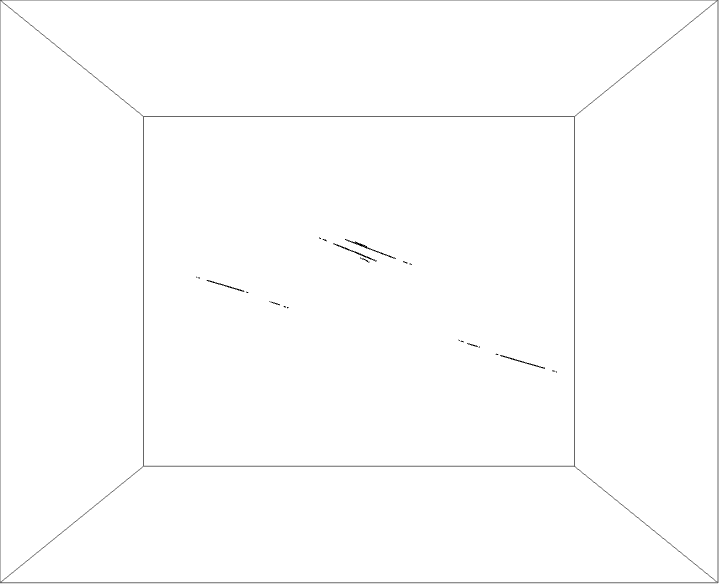
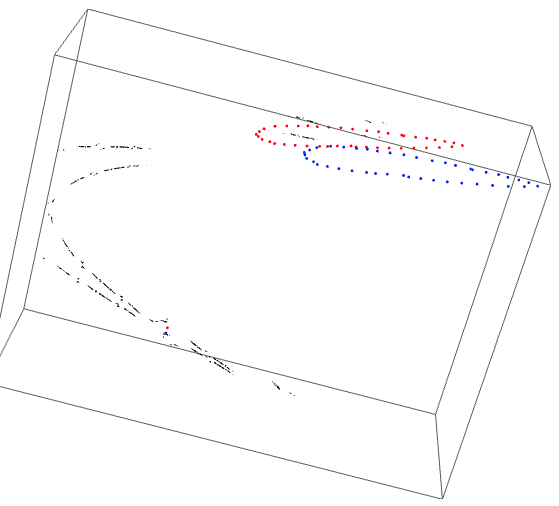
The external ray picture is shown below, with airplane portrait rays.
Critical value picture:
Traversing the loop around the AB herd

we see the following external ray picture, with airplane portrait rays:
Critical value picture:
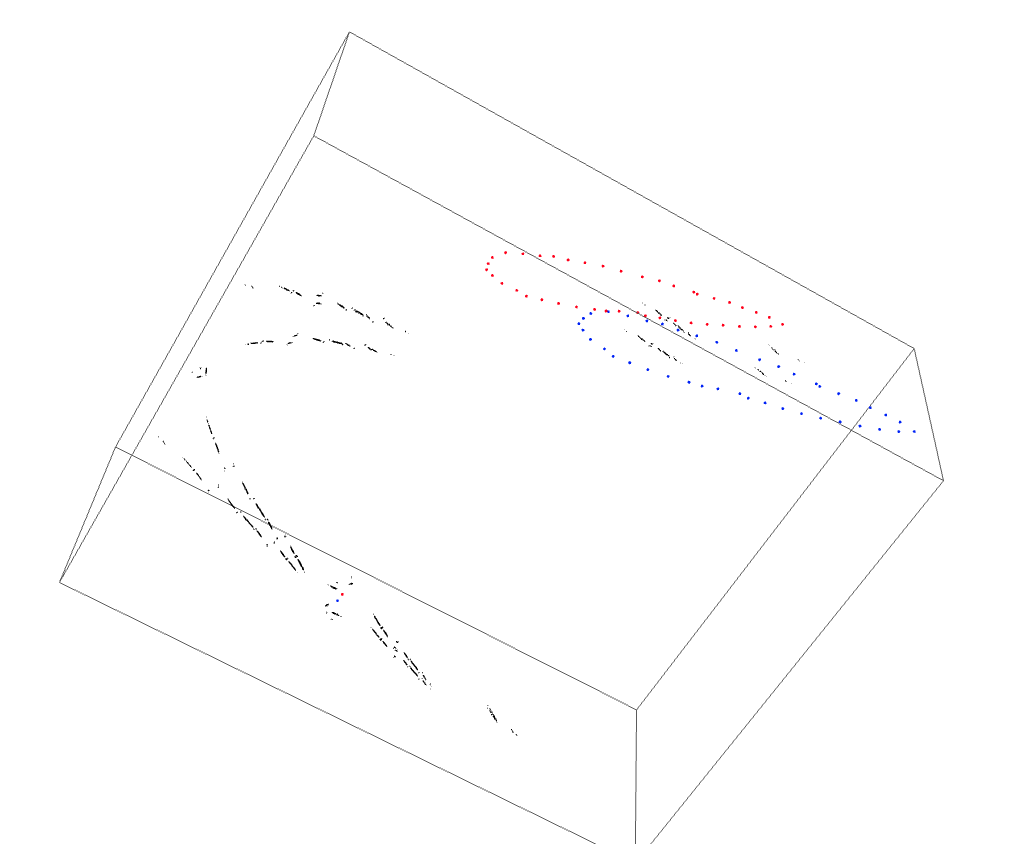
The B herd for the Koch/Tiozzo/Kokopelli wake.
We are looking at the parameter space slice $b=0.0524857 + 0.049287i$.

Traversing the loop:
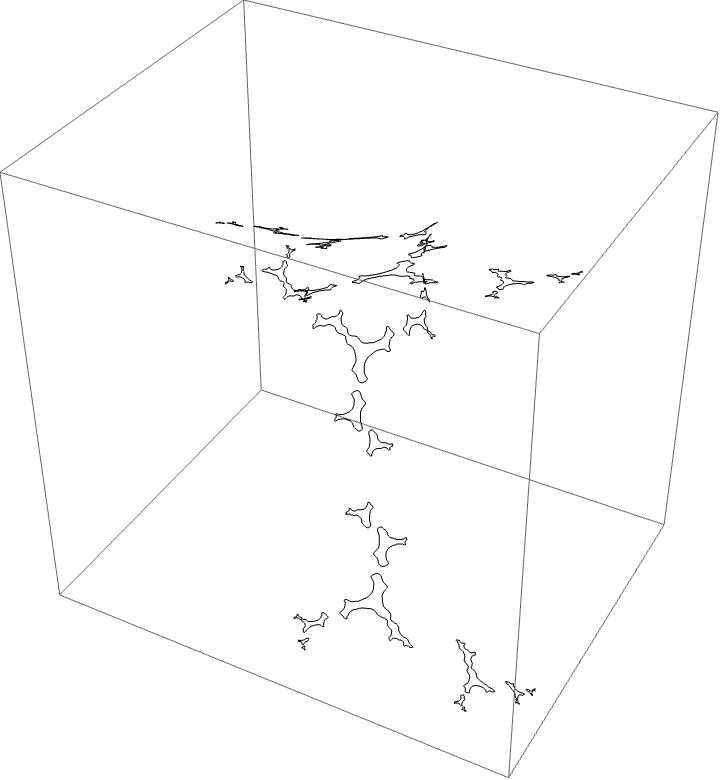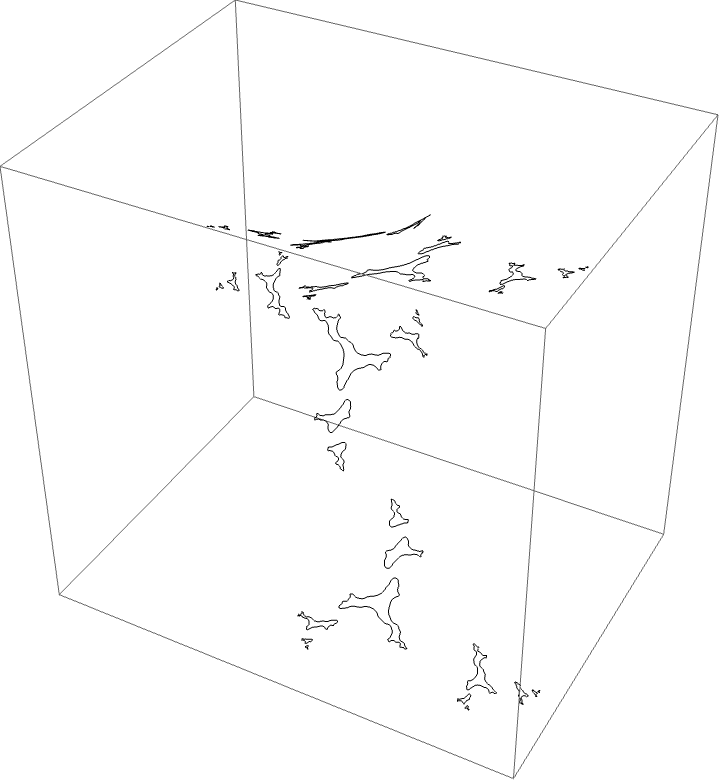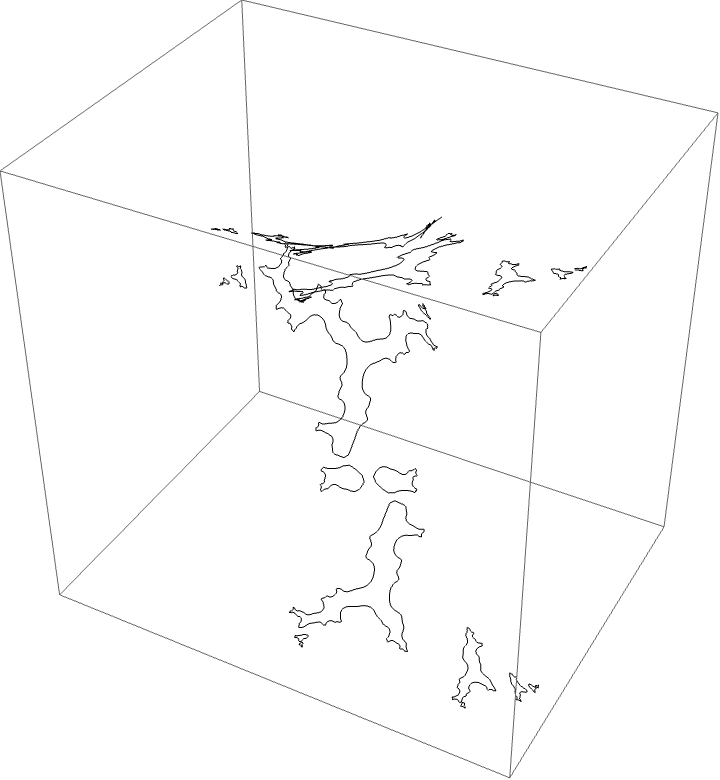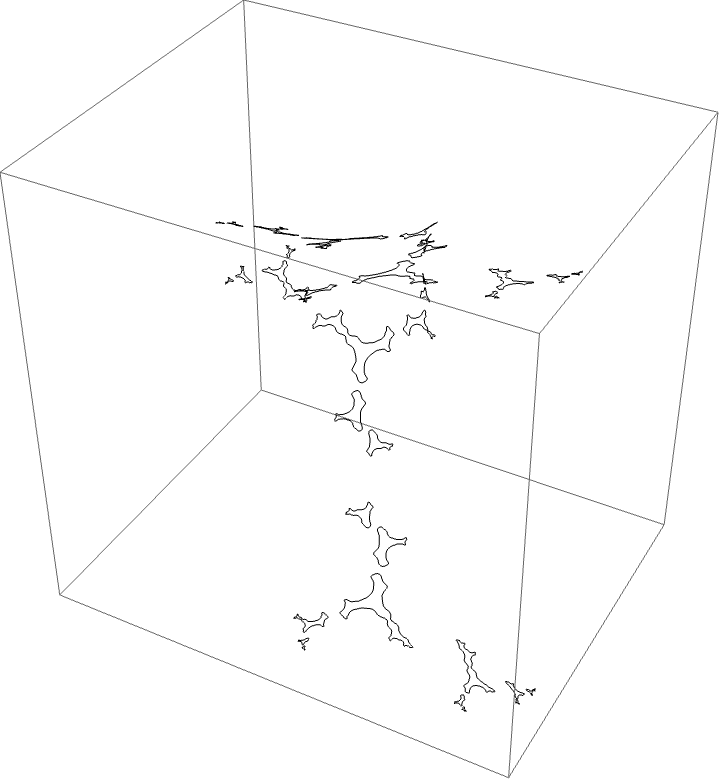
The characteristic arc is $\{3/15, 4/15\}$. The corresponding automorphism around the $B$ herd should be $B \star BBAA$. The piece with itinerary $B \star BBAA$ is bounded by rays $\{3/10, 19/60, 11/20, 17/30\}$ shown in red below.
External ray picture:
Spinning critical value:

A loop off the Basilica component
We are again looking at the $b=0.05i$ slice. We see some component breaking off. Wanted to investigate this to see if the $B \star BAA$ monodromy is seen or if we see a distinct monodromy. The characteristic arc is $\{75/127, 76/127\}$, period 7. There are no conspicuous subwakes by Lavaurs, so only one marker string. Orbit portrait has rays $\{75/127, 76/127, 23/127, 25/127, 46/127, 50/127, 92/127, 100/127,
57/127, 73/127, 114/127, 19/127, 101/127, 38/127\}$. Inserting the rays $\{75/254, 203/254\}$ gives the puzzle piece. The piece where monodromy would occur is bound by rays $\{ 165/254, 101/254, 329/508, 203/508 \}$. Kneading sequence of the wake should be BABBBAA and so the automorphism of this loop should be $B \star BABBBAA$.
The loop:

Critical value picture:
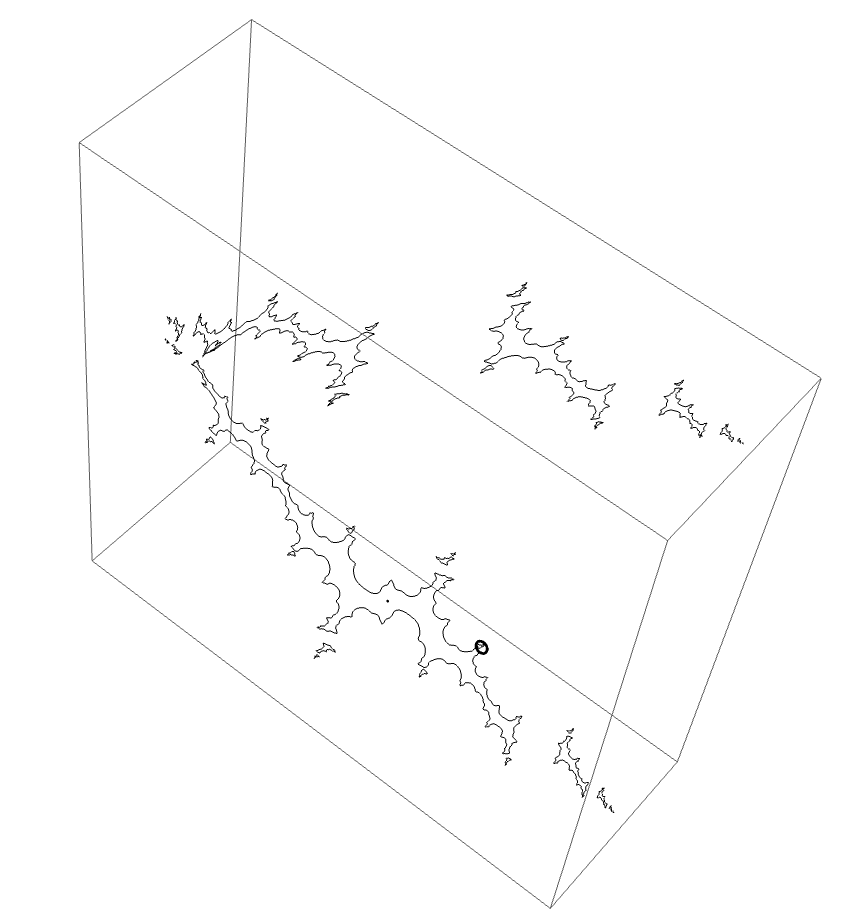
The external ray picture:
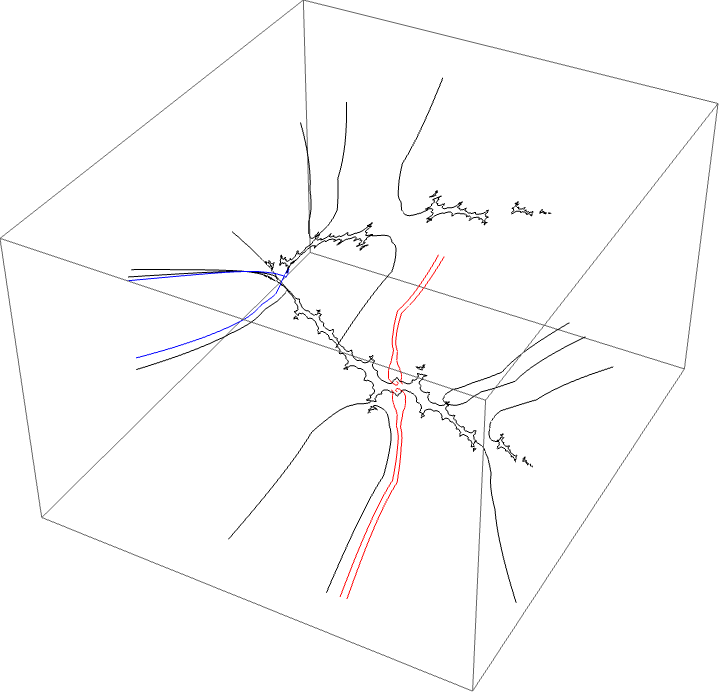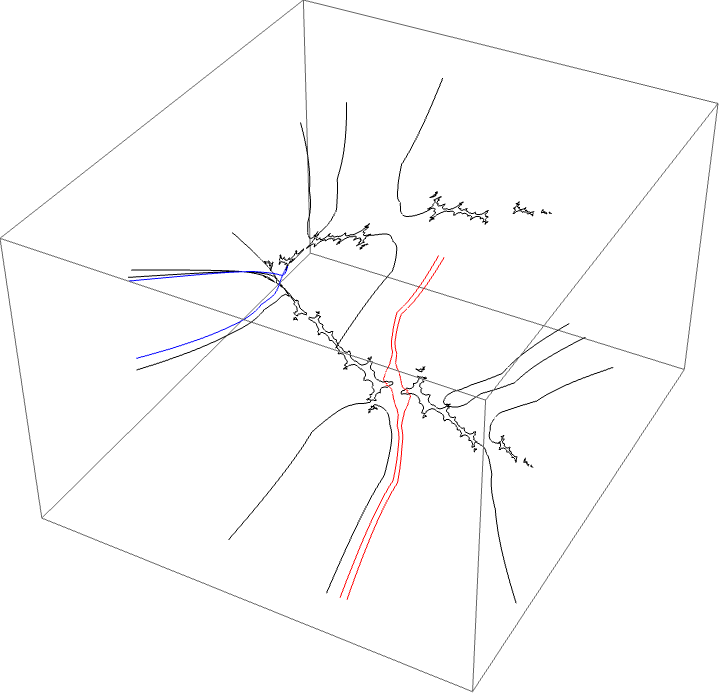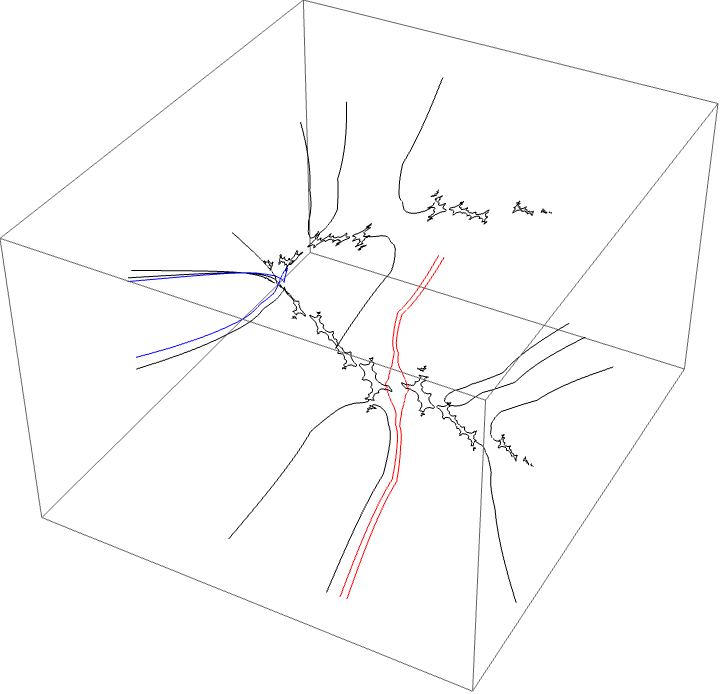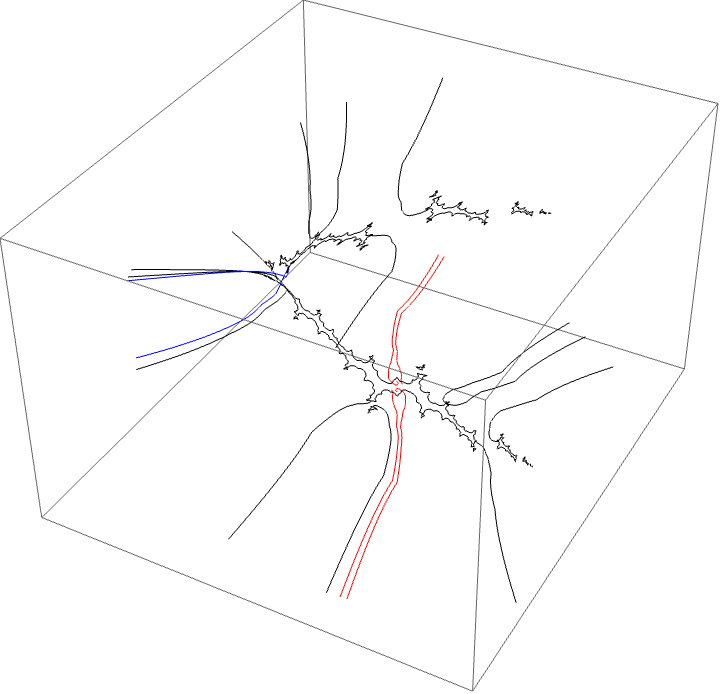
Another loop off the Basilica component
This loop comes from the wake with characteristic arc is $\{19/31, 20/31\}$. It is a period 5 hyperbolic component. There are no conspicuous subwakes by Lavaurs, so only one marker string. Orbit portrait has rays $\{19/31, 20/31, 7/31, 9/31, 14/31, 18/31, 28/31, 5/31, 25/31, 10/31 \}$. Inserting the rays $\{19/62, 51/62\}$ gives the puzzle piece. The piece where monodromy would occur is bound by rays $\{81/124, 51/124, 41/62, 25/62\}$. Kneading sequence of the wake should be BABAA and so the automorphism of this loop should be $B \star BABAA$.
The loop:

The dynamical picture:
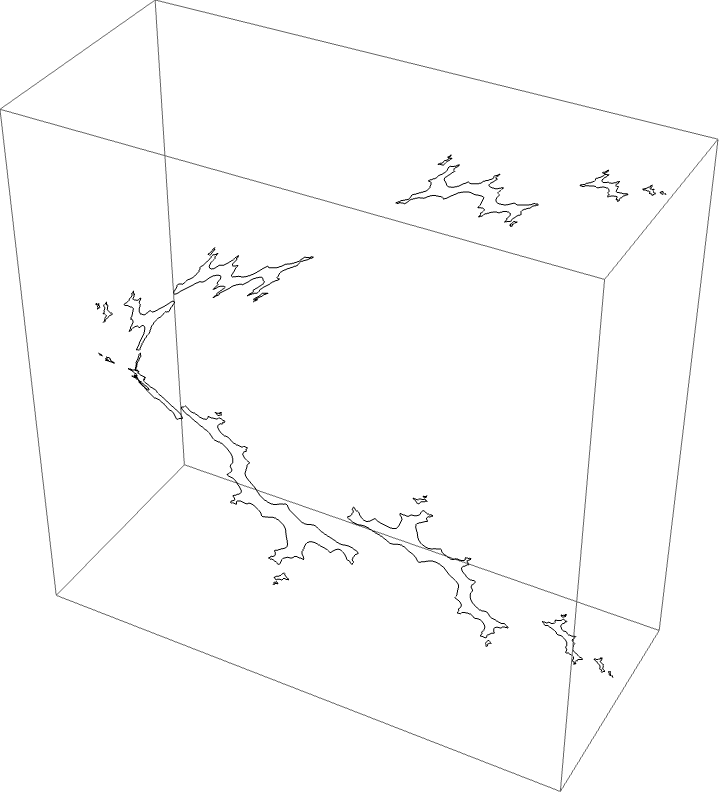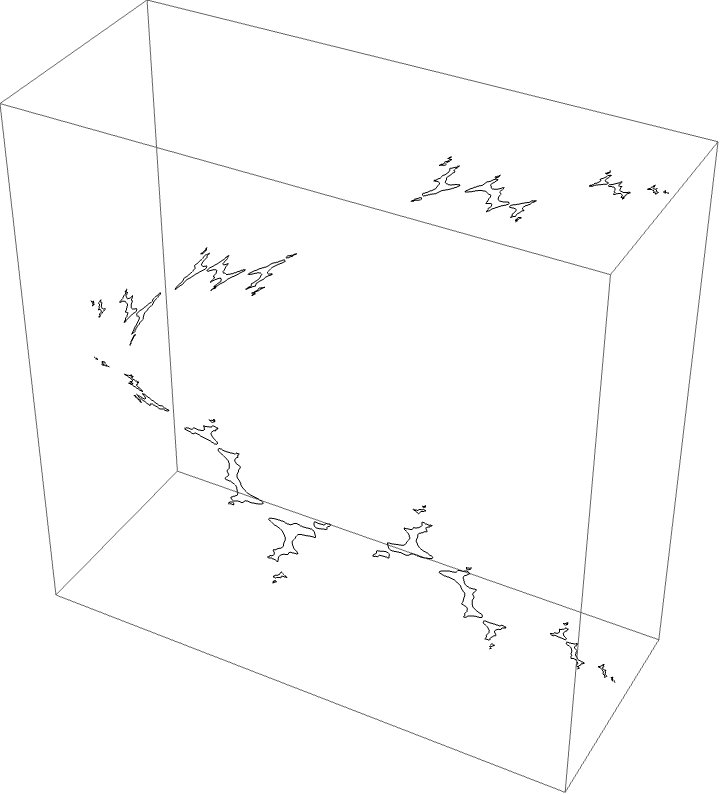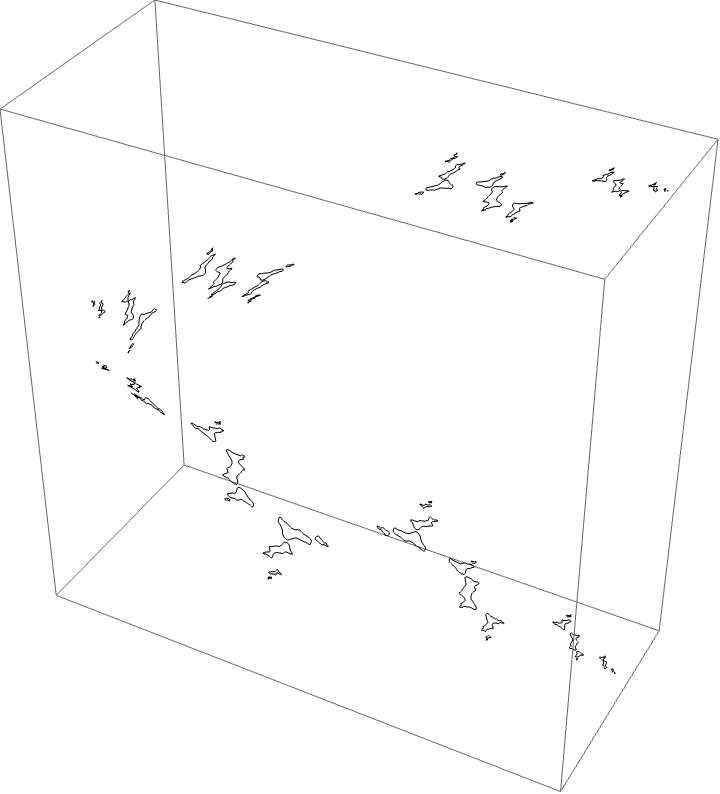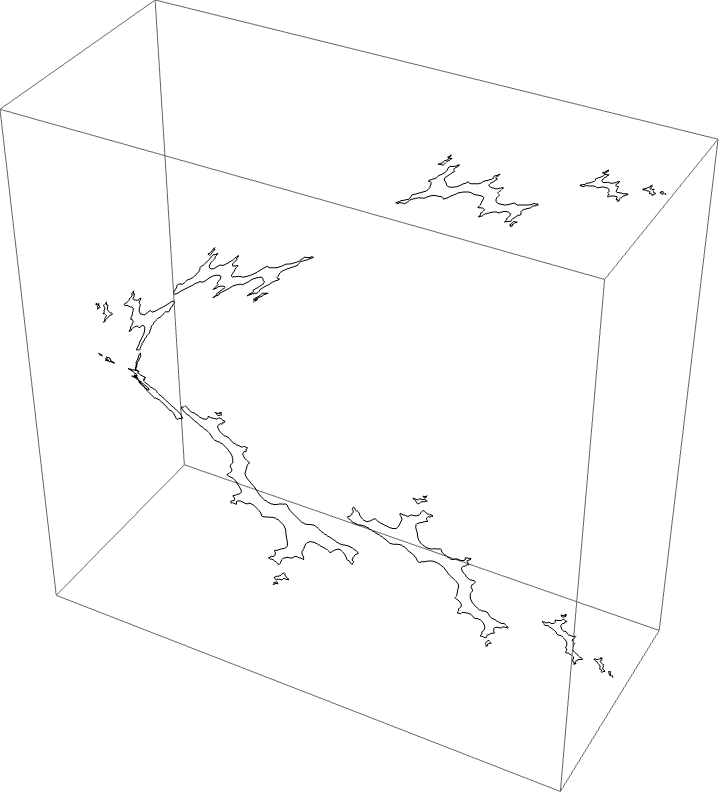
Critical value picture:

The external ray picture:
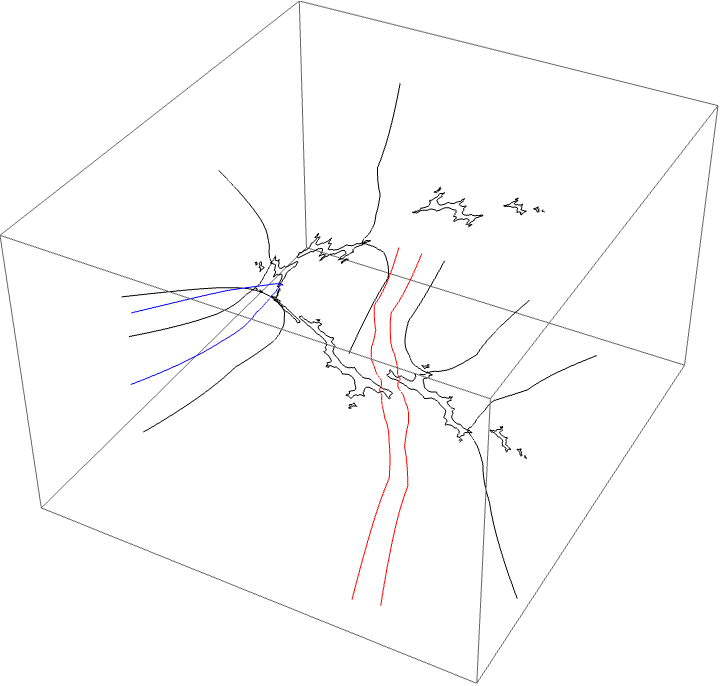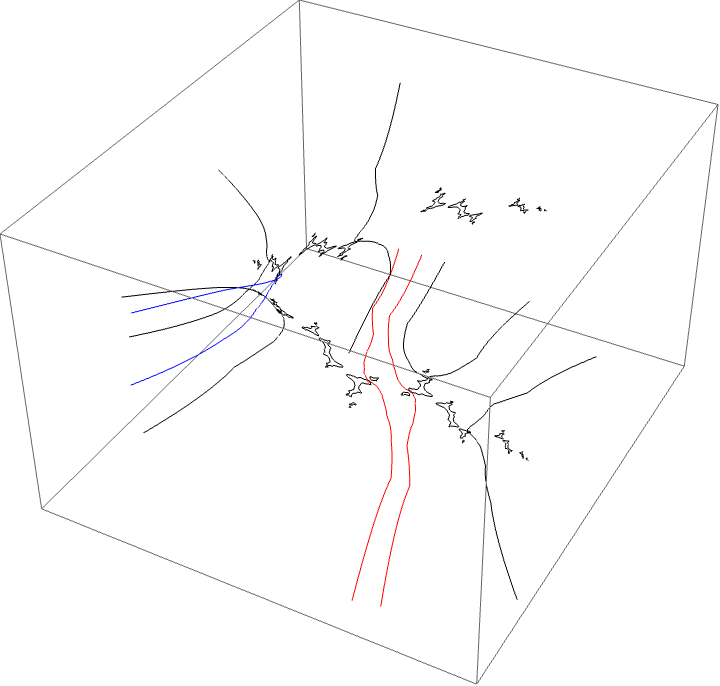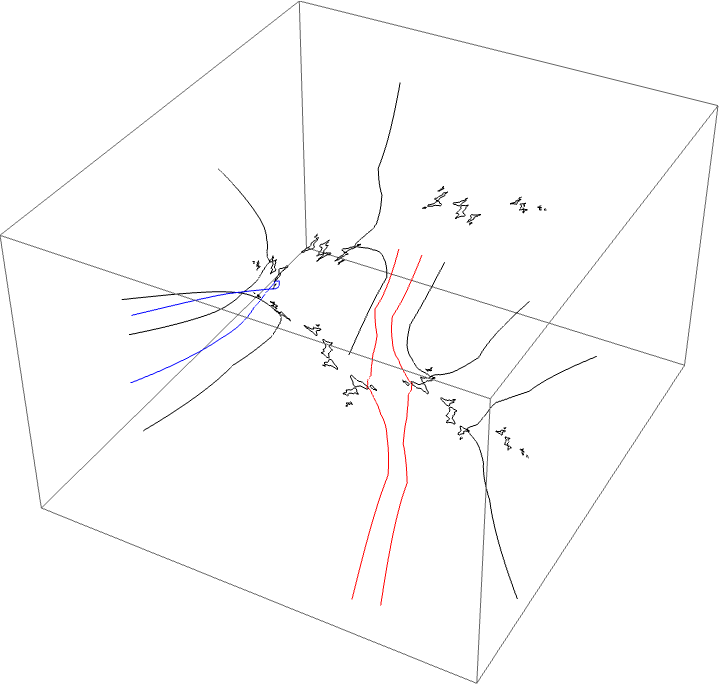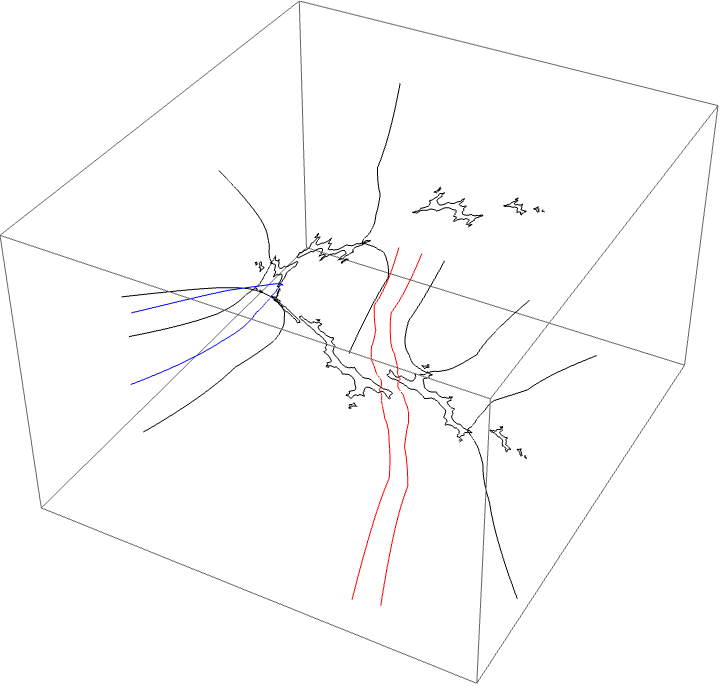
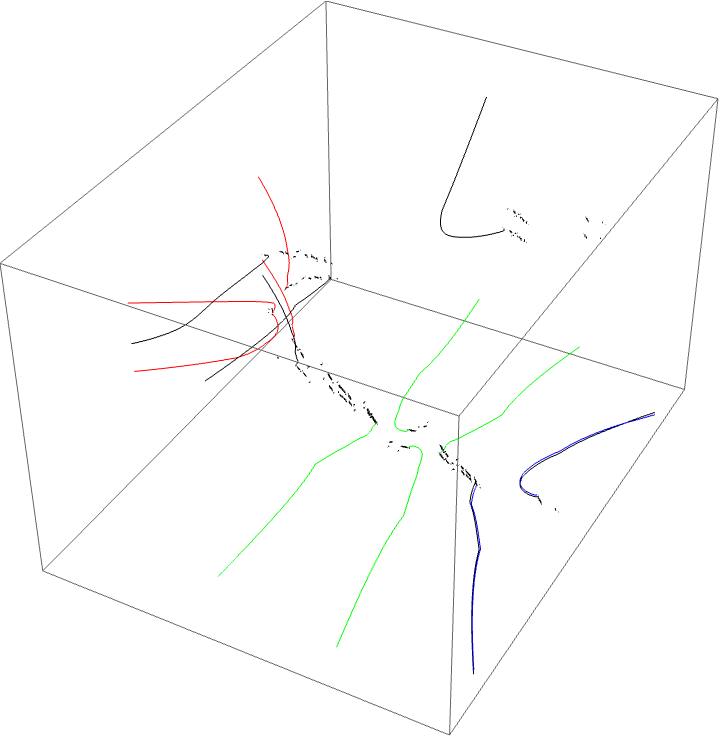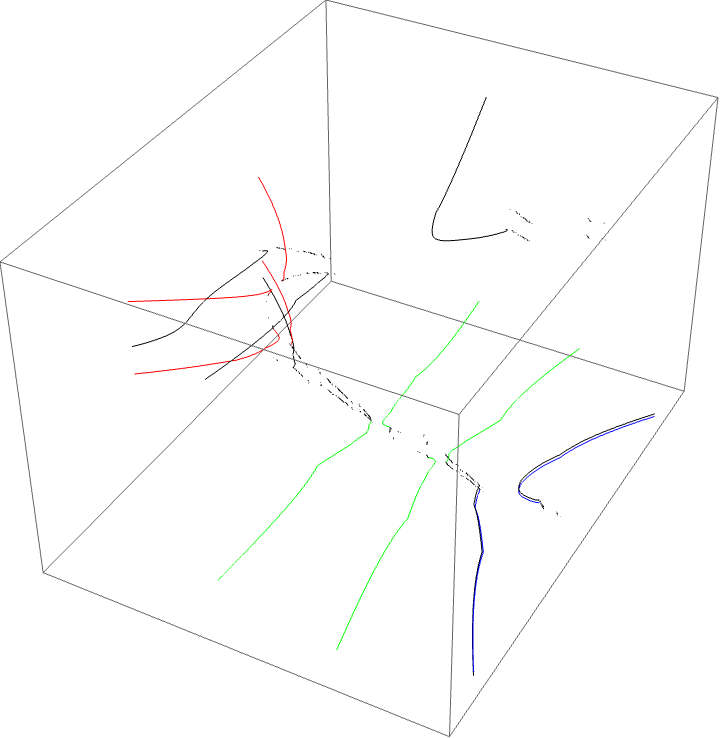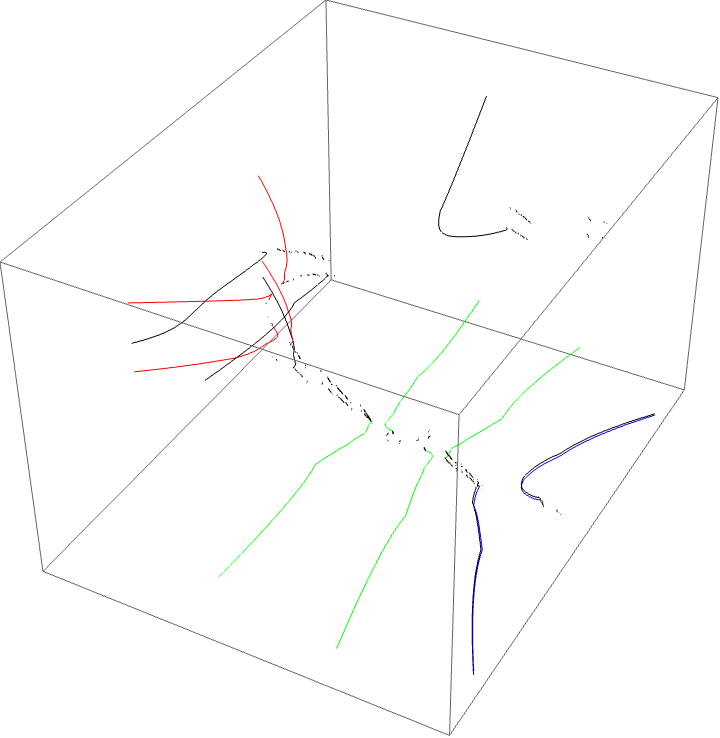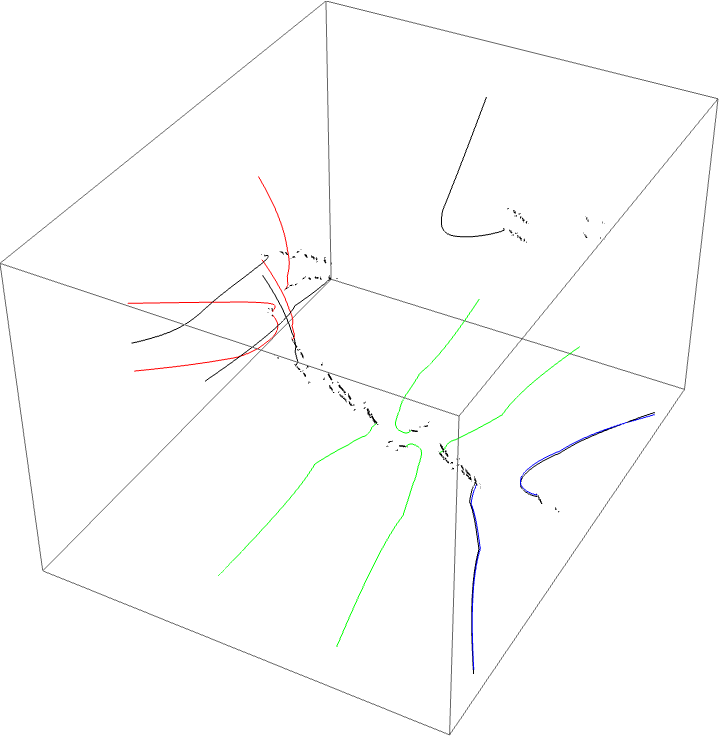
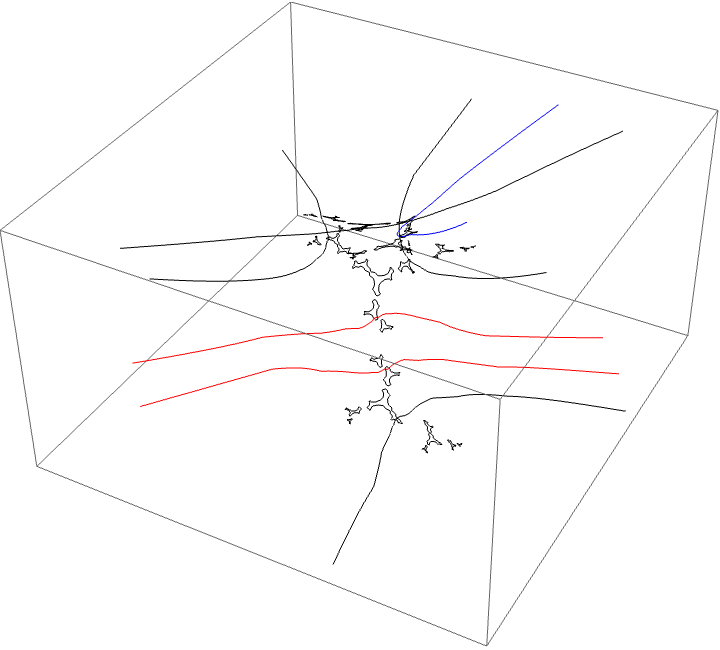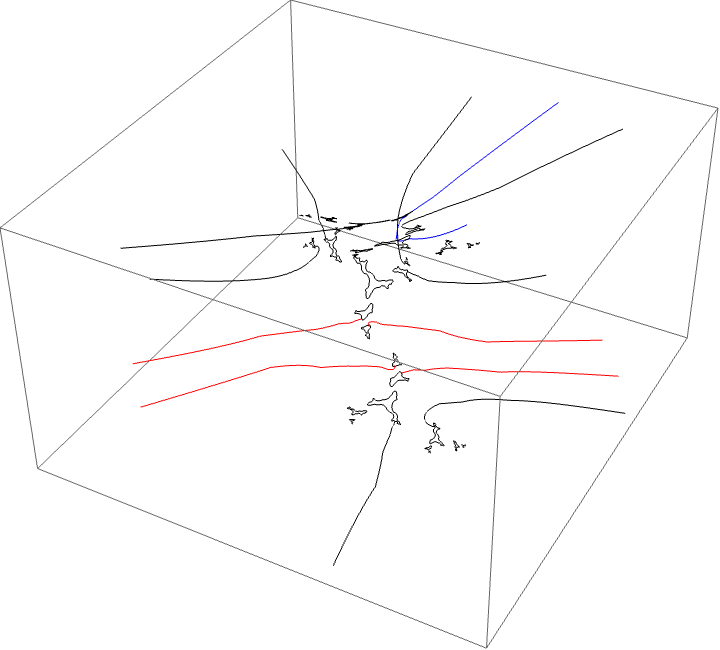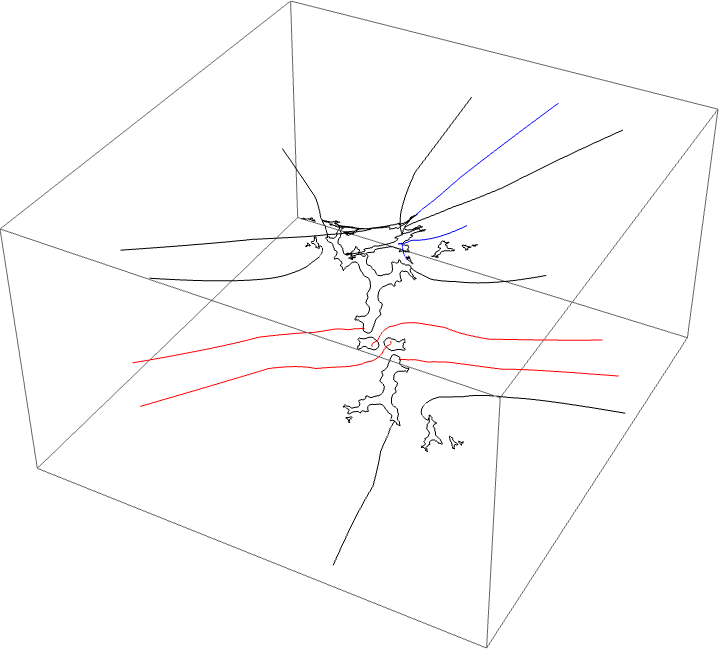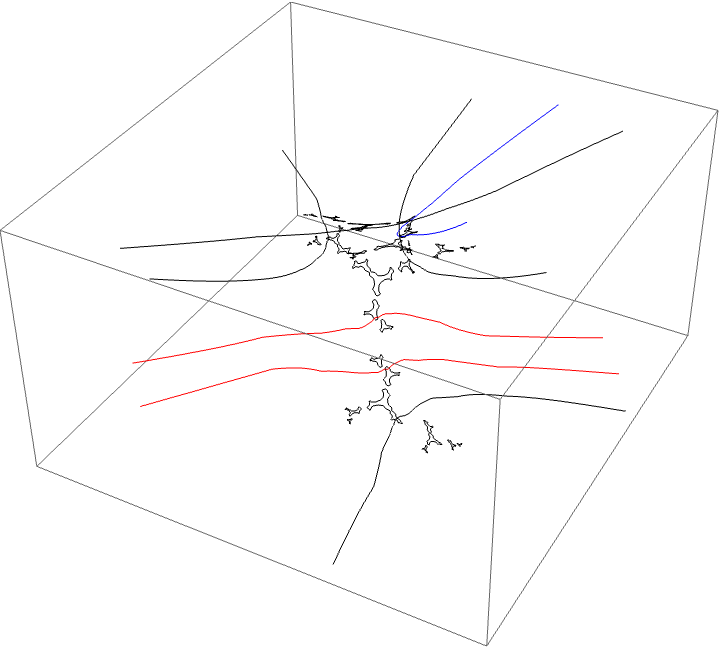
A loop around two herds from different wakes
The following loop wraps around the B herd of the airplane wake and the B herd of the BABAA. The automorphism seems to be the automorphism with markers $B \star BAA$ and $B \star BABAA$, based on the external rays. The black rays correspond to the piece with itinerary $B \star BAA$ and the red rays define the piece with itinerary $B \star BABAA$.
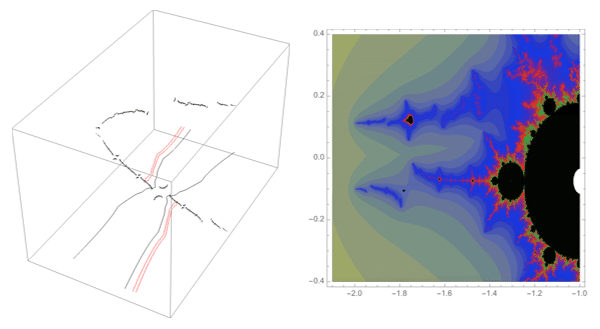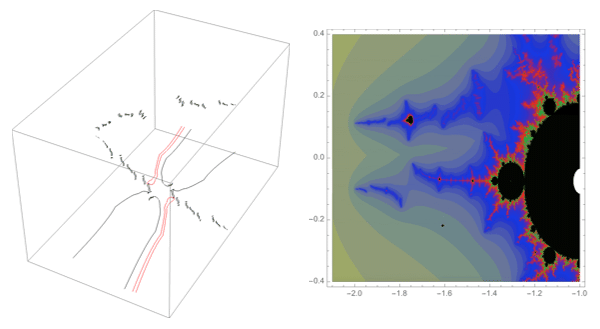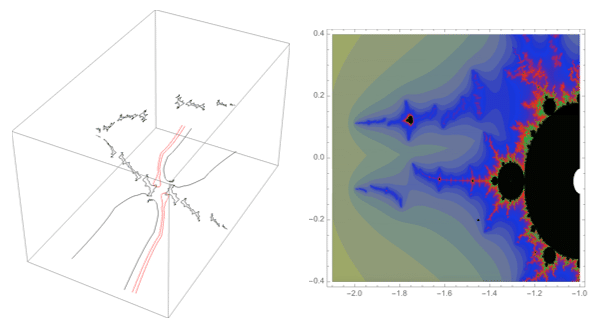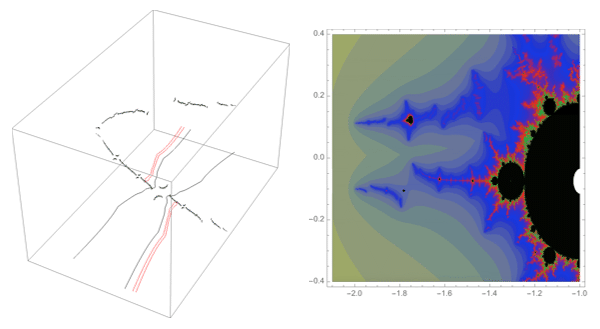
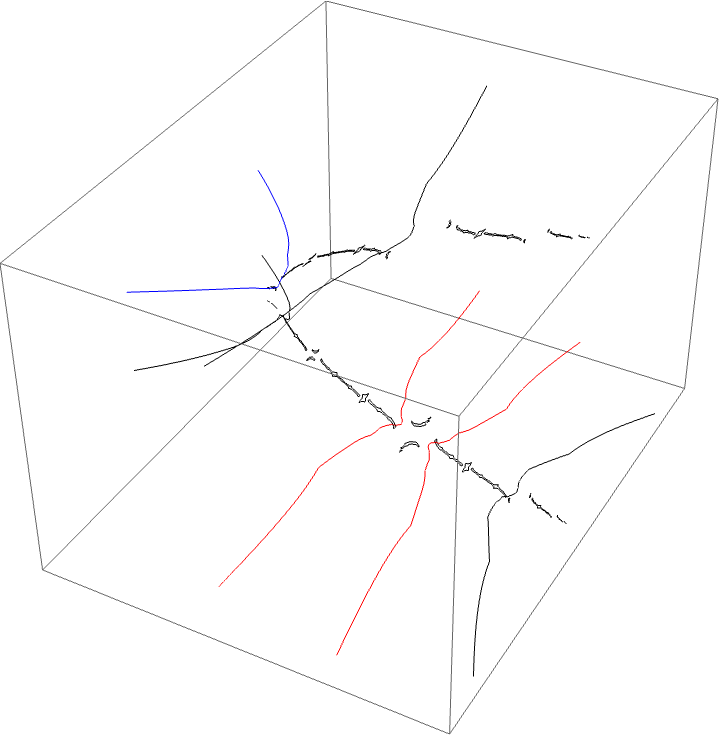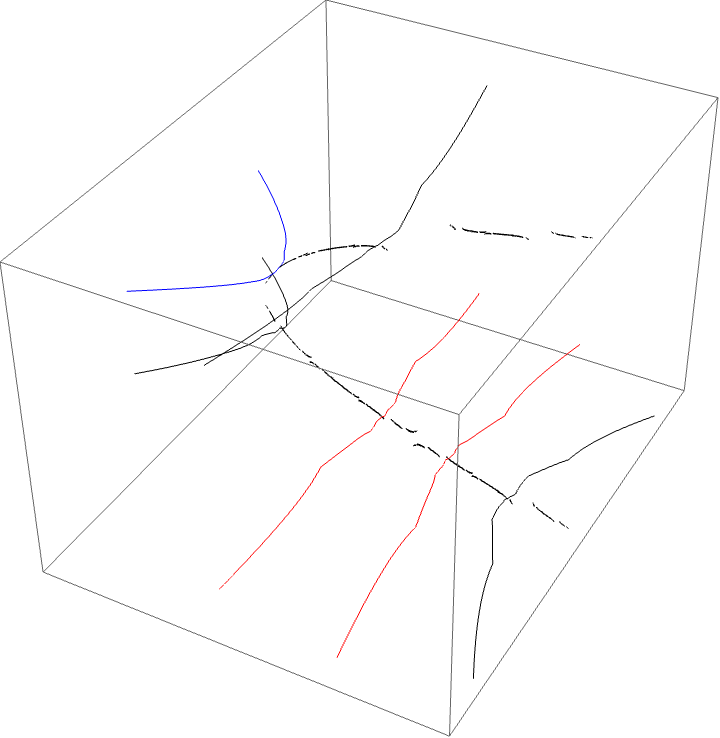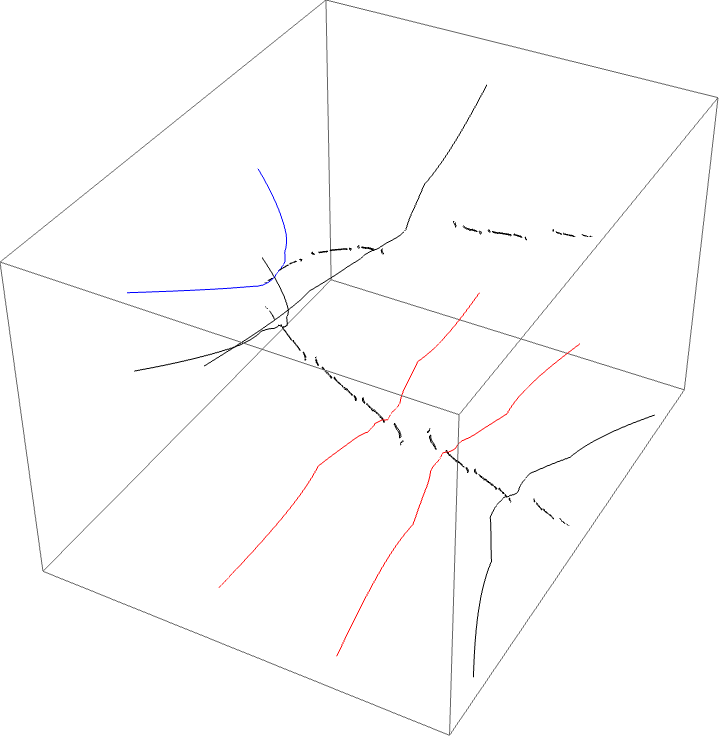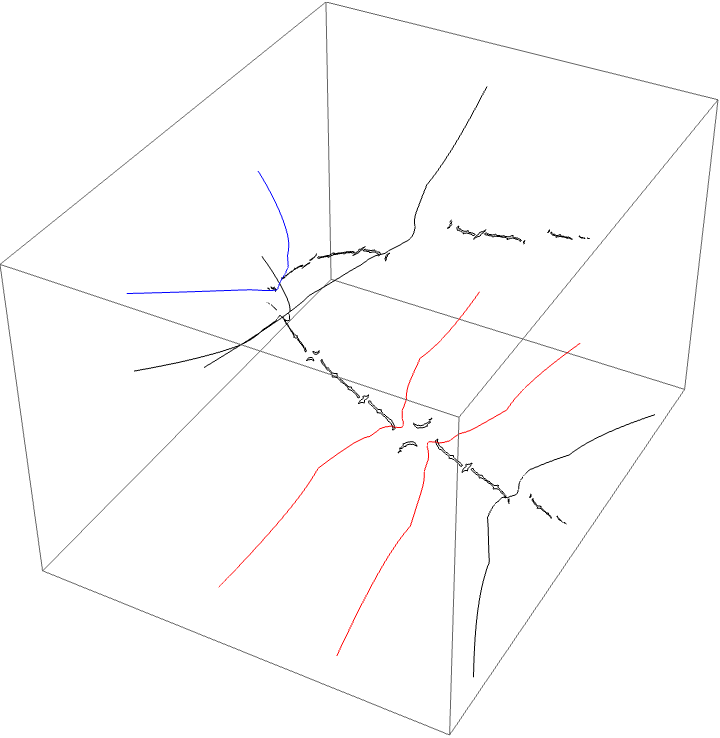
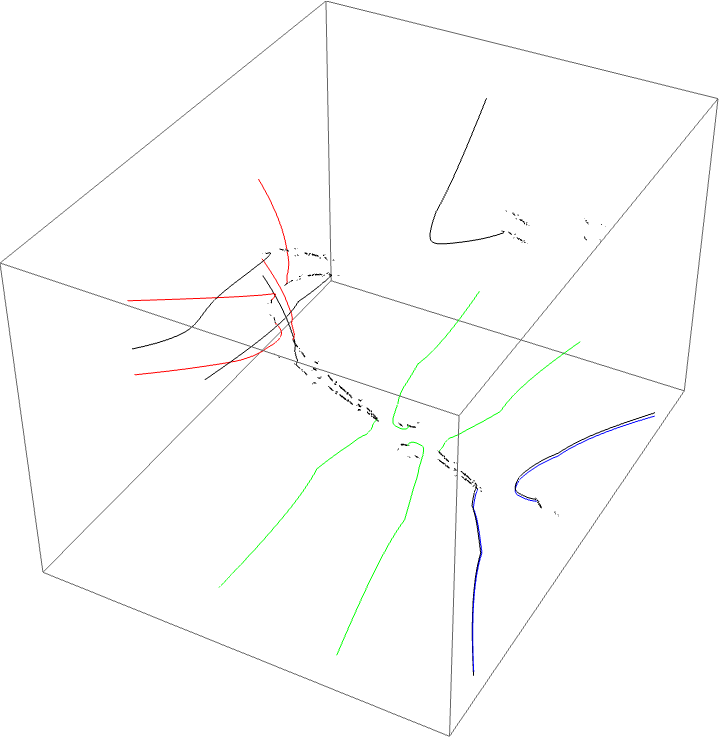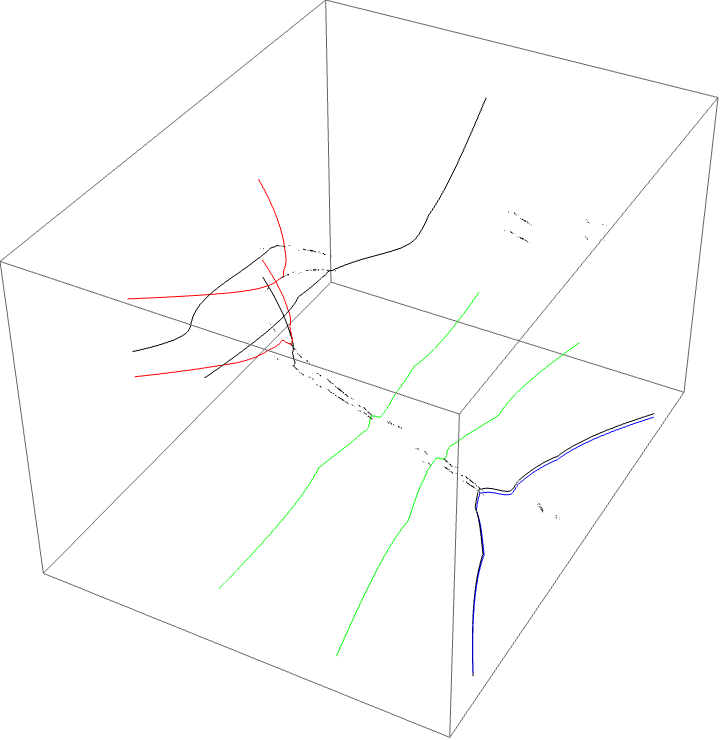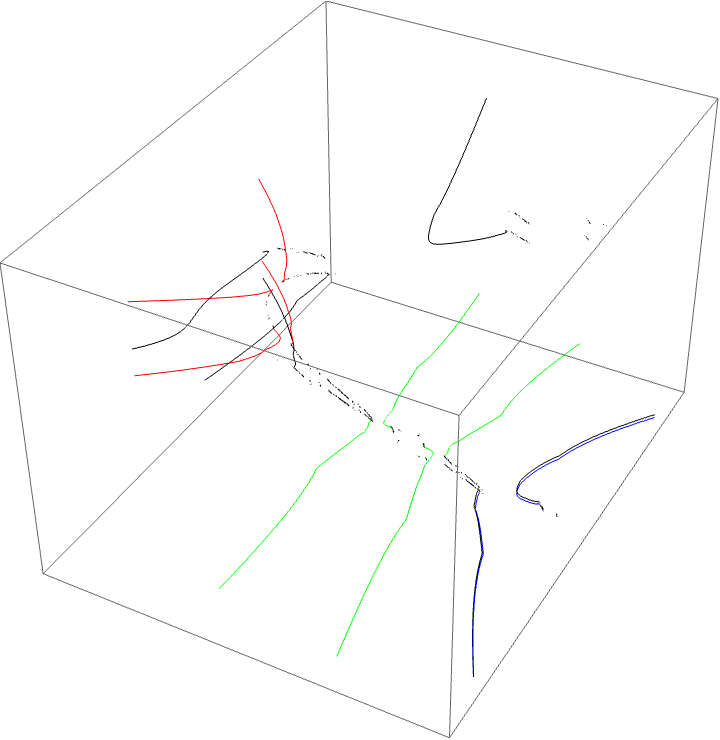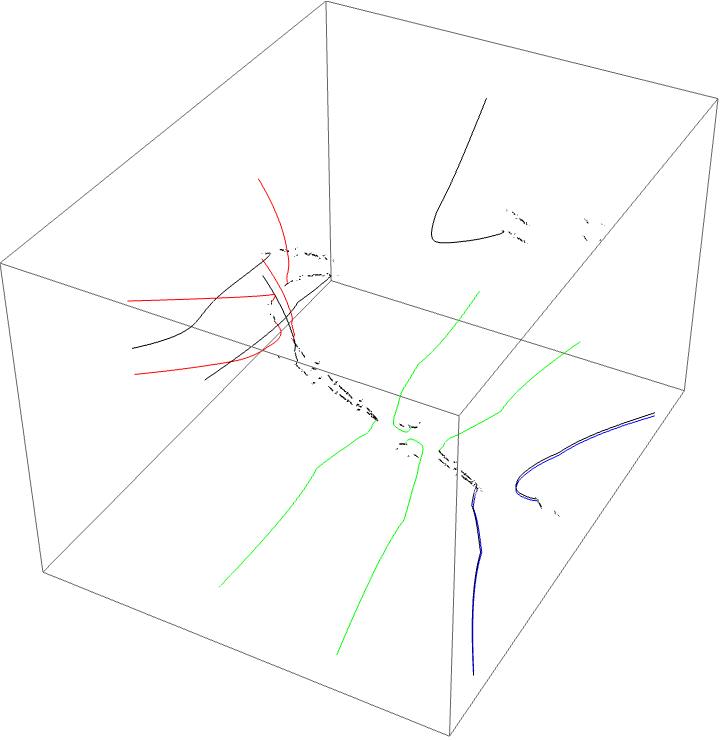
A loop around three herds from different wakes
The following loop wraps around the B herd of the airplane wake, the B herd of the BABAA wake, and the B herd of the BABBBAA wake. The automorphism seems to be the automorphism with markers $B \star BAA$, $B \star BABAA$, and $B \star BABBBAA$, based on the external rays. The black rays correspond to the piece with itinerary $B \star BAA$ with respect to the airplane partition, the red rays define the piece with itinerary $B \star BABAA$ with respect to the $BABAA$ portrait. The blue rays define the piece with itinerary $B \star BABBBAA$ with respect to the $BABBBAA$ portrait.
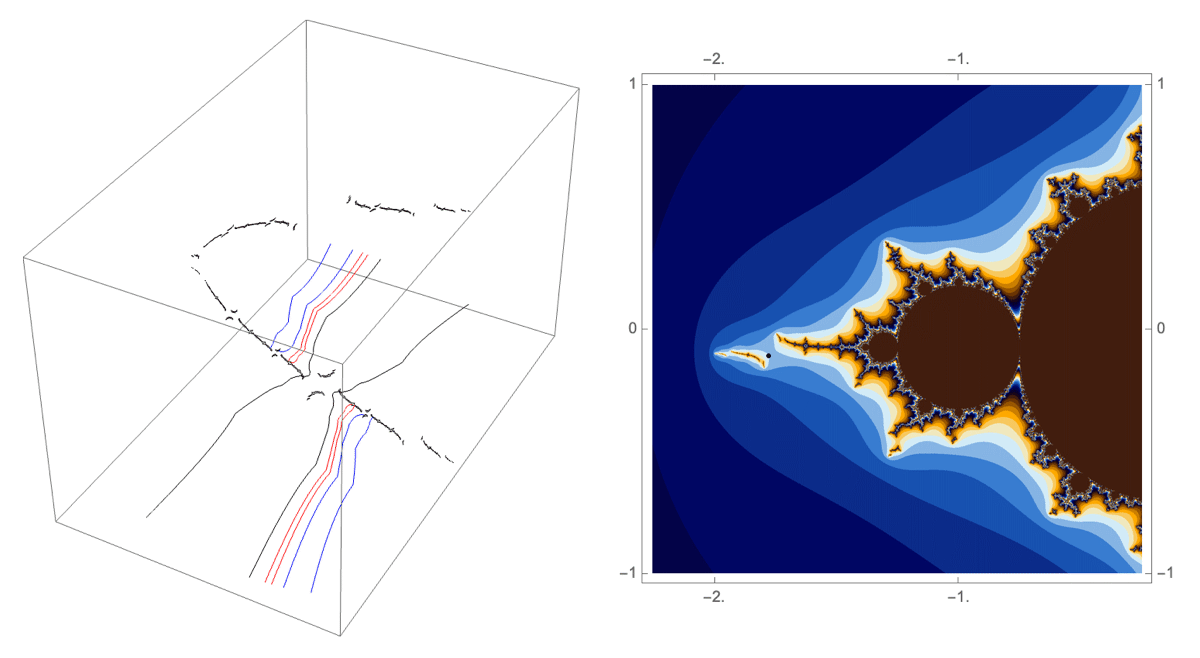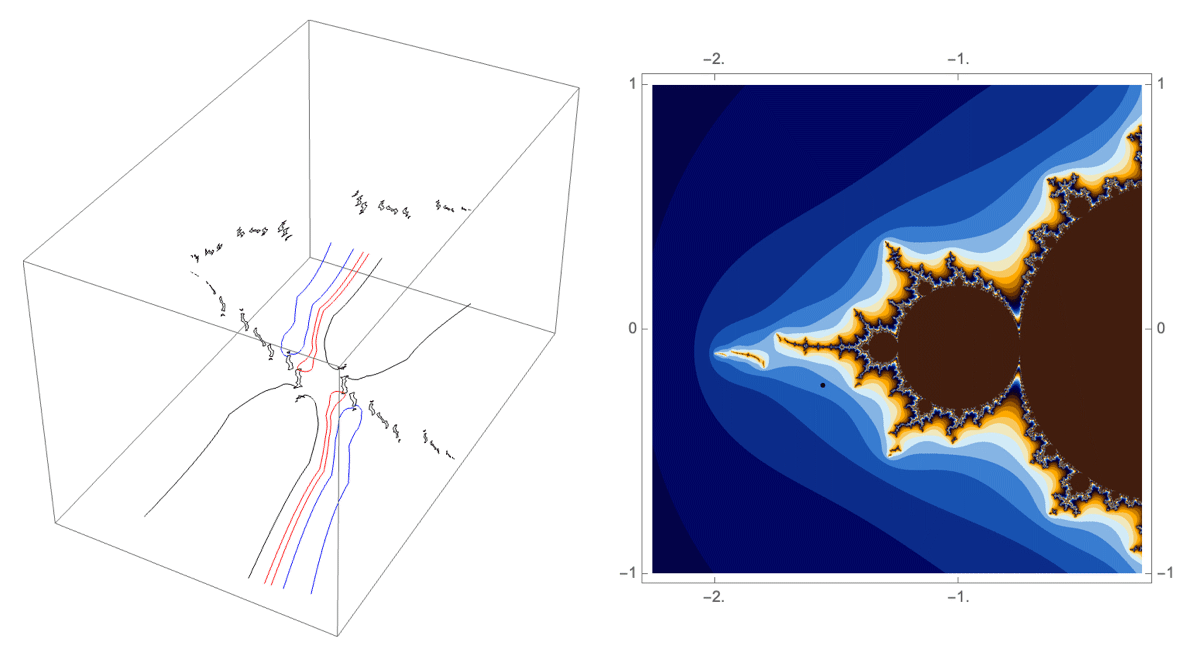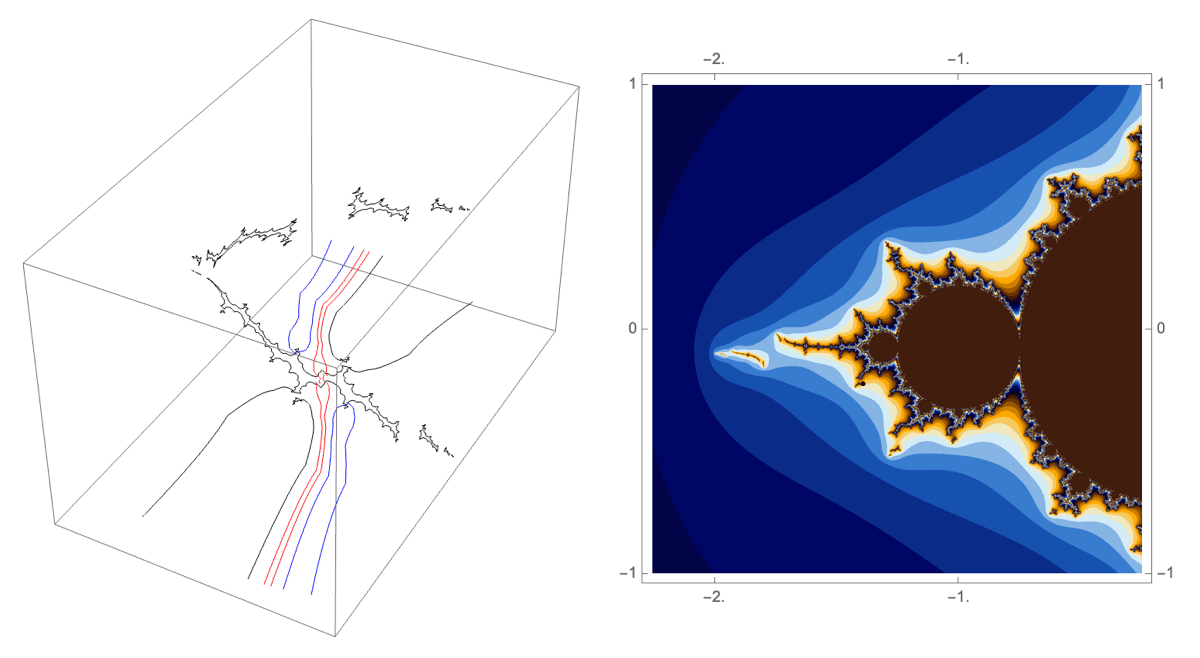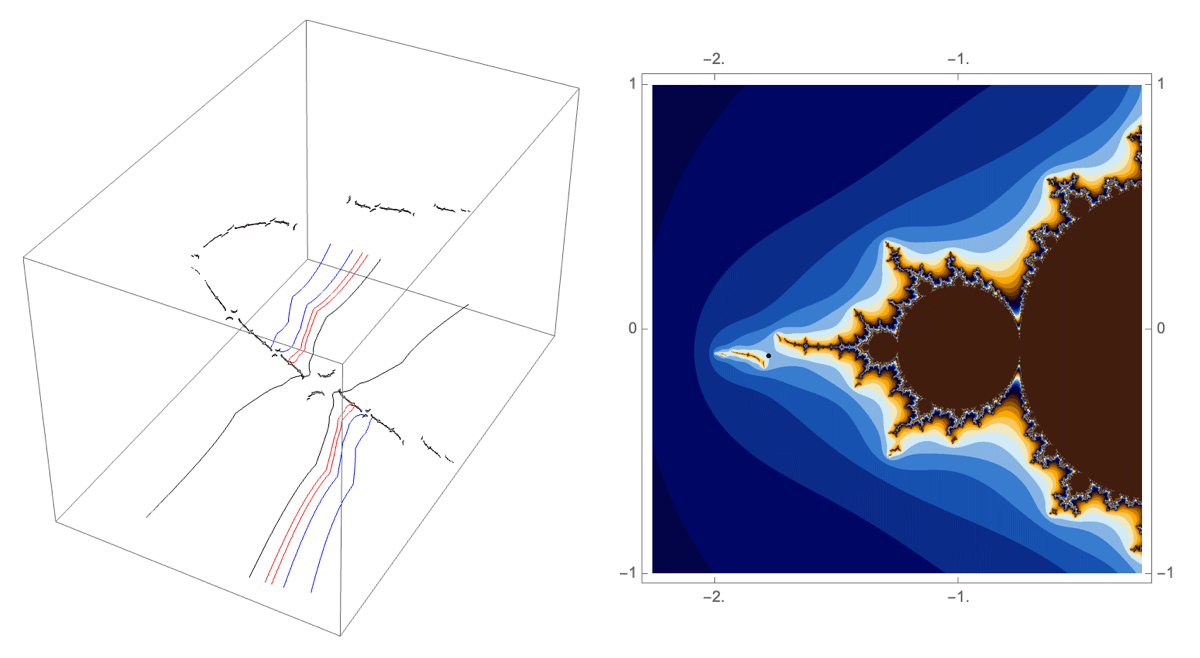
Conjecture
Suppose a loop $\gamma \in \pi_1(\mathcal{H})$ is such that $\gamma$ wraps around herds $H_i$, $i\in \{1,\cdots, n\}$ labelled by string $x_i$ associated with wakes $W_i$ with conspicuous sub-wakes $W_{i,1}, \cdots, W_{i,k_i}$. Let $y_{i,k_i} = K(W_{i,k_i})$. Then $\rho(\gamma)$ is the compound marker automorphism
$x_1\star y_{1,1}, \ \cdots, \ x_1\star y_{1,k_1},$
$x_2\star y_{2,1}, \ \cdots, \ x_2\star y_{2,k_2},$
$\cdots,$
$x_n\star y_{n,1}, \cdots, x_n\star y_{1,k_n}.$
In particular, it is the union of the marker automorphisms associated with each individual herd.
