The research area comprising computational group theory can be conveniently split up into a number of sub-areas.

Computing in finite groups

A finite group can be conveniently represented in a computer either as a permutation group or as a matrix group, usually over a finite field. The basic computational problem is to determine any structural information about the group required by the user. Currently active research problems include:

• Improve algorithms for finding automorphism groups of a group and for testing two groups for isomorphism;
• Improve algorithms for finding conjugacy classes of maximal subgroups in a group;
• Develop methods to set up an explicit isomorphism between an arbitrary representation of a finite simple group and the "natural" representation of that group.

Some of the problems in this area represent interesting and challenging problems in complexity theory for computer scientists.

Computing with finitely presented group

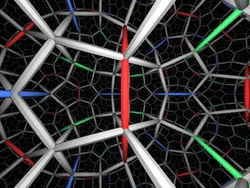A tessellation of hyperbolic 3-space by dodecahedra - symmetry group is automatic

Classical algorithms, such as Todd-coxeter coset enumeration, aim to find finite quotients of the group in question and to represent these quotients in a form suitable for the use of the methods described above for finite groups.

More recent algorithms, and specifically the automatic groups packages that were developed and implemented at Warwick, aim to carry out basic operations efficiently in infinite groups. These include reducing words to a normal form, solving the conjugacy problem, and testing for membership in a subgroup that could have infinite index in the original group. This is currently the most active and interesting field of research in computational group theory at Warwick.

Connections with computer science

The problems involving complexity theory coming from finite groups were already mentioned above. The research into automatic groups has led to interesting connections with formal language theory. For example, what is the relationship between the formal language class of the set of words that represent the identity in a finitely generated group and the algebraic structure of that group? This has been answered for the classes of regular and context free languages, but only partially for more general classes such as the context sensitive languages.

Computational Packages

The GAP and MAGMA computational algebra packages, which specialise in computational group theory, are both available at Warwick, and research in this area at Warwick is carried out in close collaboration with the administrators of these packages.