Understanding the properties of crystalline materials, such as metals, has been a central part of humanity's march of technological advancement since the end of the Stone Age. However, despite thousands of years of practical experience, the microscopic mechanism by which metals deform was only discovered in the first decades of the 20th century: Volterra and Taylor correctly identified the movement of defects in the crystal lattice, in the form of so-called "dislocations", as the fundamental process that allows crystalline solids to deform. When a dislocation moves, it causes a net displacement of crystal planes and thus a (very small) deformation of the macroscopic specimen; see Fig. 1 for an illustration. You could not bend a spoon if not for the movement of dislocations!

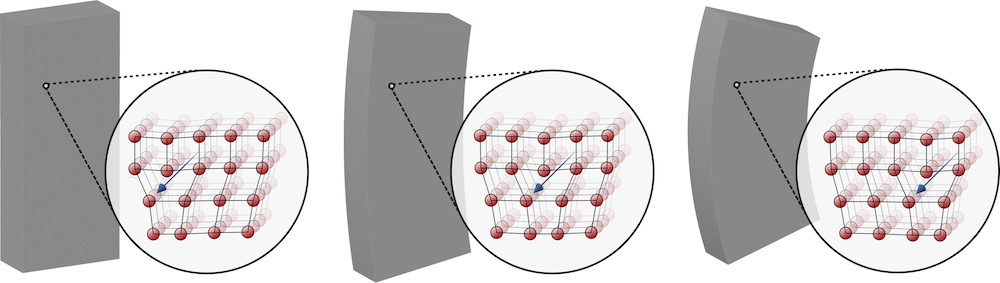
Fig 1 - Dislocation movement as the mechanism of plastic deformation.

Yet, despite a century of research, we still do not have a comprehensive, reliable, and rigorous theory that describes the plastic deformation of macroscopic crystalline solids from its micro-mechanical principles. This goal is of such practical, as well as theoretical, importance that it is sometimes referred to as the “Holy Grail” of Solid Mechanics.

Questions such as these have a mathematical counterpart in the study of so-called “diffusely concentrating” sequences of functions; see Fig. 2 for some examples.

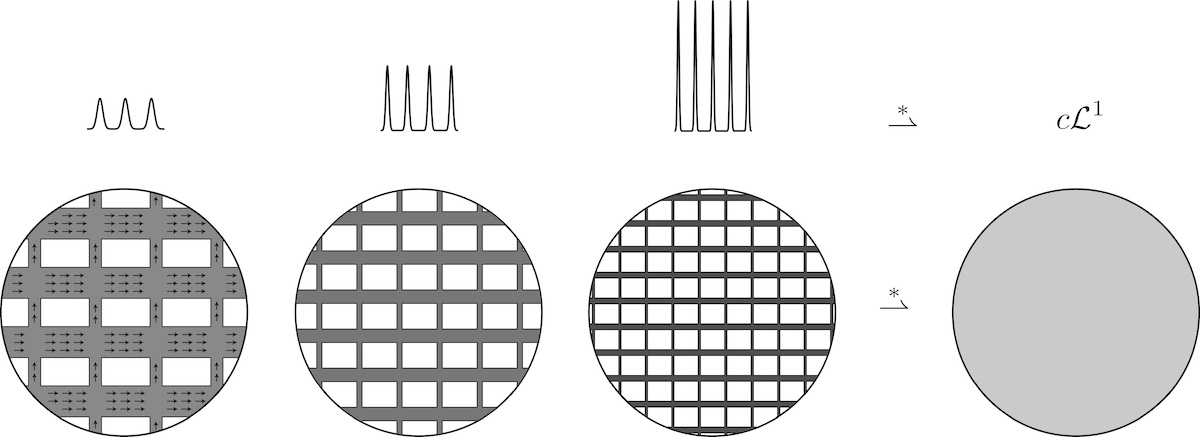
Fig 2 - Examples of diffuse concentrations

The study of these singular structures poses many challenges and complications. For instance, dislocation defects always occur along curves, which can get "entangled" with each other like spaghetti in a bowl, directly affecting the properties of the material. When one tries to understand the movement of such entangled dislocations, new types of singularities, related to the well-known "devil's staircase" of Cantor, can form and need to be understood thoroughly, for instance the "flat mountain singularity" illustrated in Fig. 3.

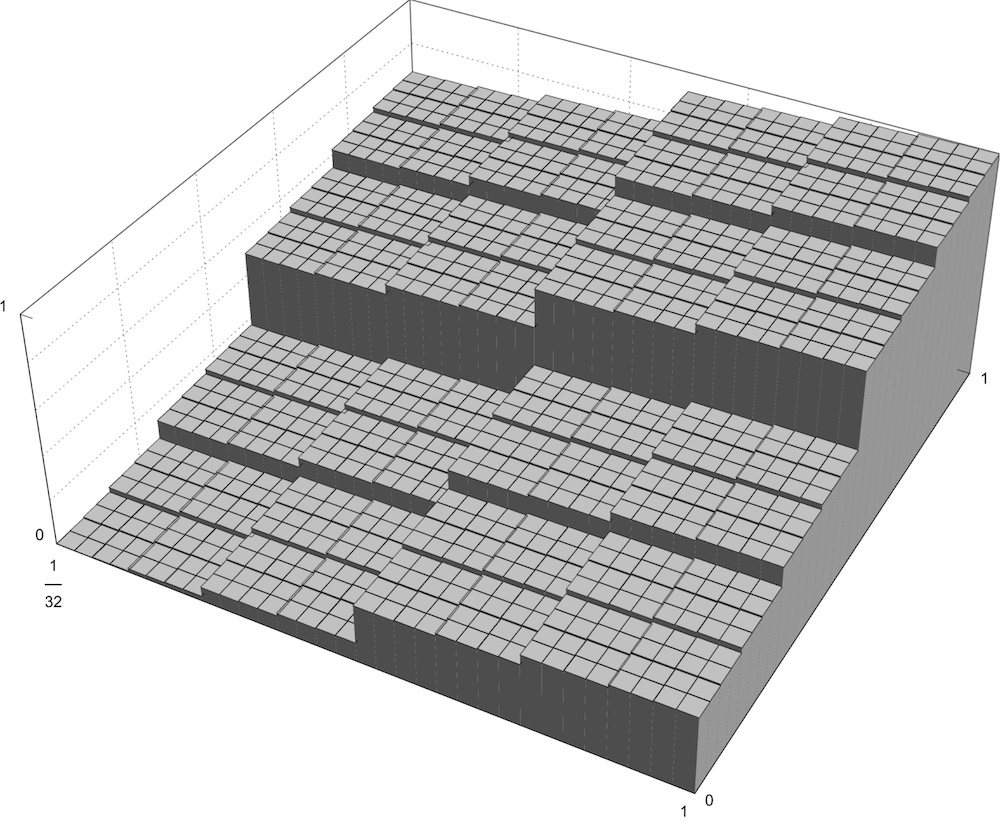
Fig 3 - The flat mountain singularity

Moreover, a very large number of dislocation defects are usually present, hence a "field description" is desirable to avoid having to consider all these lines separately. But how can one effectively describe a "field of lines" without losing crucial bits of information? Such a model of dislocation fields and the resulting plastic dynamics has so far proved elusive.

The research into these theoretical challenges and their applications will be greatly advanced by £1.75 million of funding from the European Research Council (ERC) through an ERC Consolidator Grant to Prof. Filip Rindler of the Warwick Mathematics Institute. While predominately sitting at the intersection of the theoretical fields of Nonlinear PDE Theory, Geometric Measure Theory, and the Calculus of Variations, applications to Solid Mechanics and Theoretical Material Science will also form a crucial part of this research programme.

Prof. Rindler comments: “In my research, theoretical investigations in Mathematical Analysis go hand-in-hand with applications to Material Science: Abstract mathematical techniques yield new insights into concrete physical problems, which in turn serve as inspiration for the development of new theories. This generous funding will allow me to build a strong group to tackle these pressing open problems.”