Seeing crystal symmetry with D-LACBED
Selected Area Diffraction Patterns

A selected area diffraction pattern (SADP) is collected using a parallel beam of electrons, giving a pattern of sharp spots. The region of the sample which contributes to the diffraction pattern is selected using an aperture. Since multiple diffraction effects redistribute diffracted intensity from strong beams into weaker ones, it is not possible to use the intensities of the beams to determine symmetry. However the positions of the spots and the geometry can be used. The pattern above is from Na0.5Bi0.5TiO3 , a piezoelectric material with a tilted perovskite structure which is almost cubic - it is in fact rhombohedral with alpha = 89.93 degrees. It is not centrosymmetric. None of these details are visible in the above SADP.
, a piezoelectric material with a tilted perovskite structure which is almost cubic - it is in fact rhombohedral with alpha = 89.93 degrees. It is not centrosymmetric. None of these details are visible in the above SADP.
Convergent Beam Diffraction Patterns

More detail can be seen in convergent beam diffraction patterns, since they show the variation in diffracted intensity over a ange of incident beam angles, and the symmetry can be determined (the seminal paper of Buxton, Eades Steeds and Rackham, Phil. Trans. Roy. Soc. 281, 171 (1976) can be found here). While CBED is excellent for some materials and is still the method of choice for symmetry determination, here it is not possible to see enough detail in any of the discs even to be sure if the crystal is aligned near the zone axis.
Digital Large Angle Convergent Beam Patterns
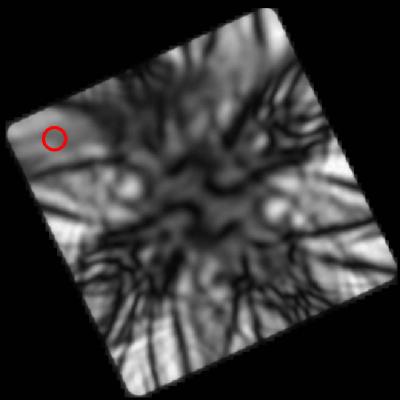
By combining lots of individual patterns acquired using computer control of beam tilt, it is possible to cover a much wider range of angles for the incident beam, as shown above. The red circle shows the size of a disc in one of the CBED patterns. Now it is possible to see the centre of the pattern. The 000 disc always has at least 2-fold symmetry - but it is obvious here that the mirror symmetries that would exist in a cubic material are not present.

As described on other pages, D-LACBED gives lots of different beams at once. Here the lack of inversion and mirror symmetry is now very clear.
For Perovskites, the point group must be a sub-group of the high temperature cubic phase: