Hopf solitions (after Heinz Hopf) are topological solitons with a non-trivial hopf invariant (charge). We are interested in their occurence in field theories. Suppose we are concerned with a field theory, taken as a continuous map, . As in, for example, the O(3) sigma model. We are interested in the effects of imposing the (natural) boundary condition: .

Now since this boundary condition gives us a homogeneous field at infinity we can perform a single point compactification of three dimensional space to arrive at a map

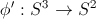
explicitly this can be done by e.g. inverse stereographic projection. We can now investigate the topological properties of this map. Specifically our map will represent an element of the group

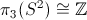
What this means is that for any field configuration, we can associate an integer (the Hopf charge). For configurations with this non-zero we say that we have a Hopf soliton. Since these are topological invariants, this charge is a constant of the dynamics provided no singularities are introduced into the field.