The History of Chinese Mathematics
Introduction
Throughout history, mathematicians from various regions have made significant contributions to the field, bringing new innovative ideas, challenging Eurocentric notions and enriching the global mathematical landscape. One great example of such is China, which has produced ground-breaking work, often surpassing European mathematicians.
Ancient Chinese Mathematics
Chinese civilisation boasts a rich history in mathematical achievements that date back thousands of years. It is important to recognise the advancements in Chinese mathematics, particularly ones which were overshadowed by their European counterparts.
Shang Dynasty (1600 BC - 1050 BC)

Oracle Bones
Oracle bones offer a glimpse into the ancient civilization that flourished over 3,000 years ago. They were usually made out of ox bone or turtle shell[1] and characters were directly carved onto them, mainly for religious divination.
Beyond their role as divinatory tools and insights into ancient Chinese society, oracle bones hold intriguing connections to the world of mathematics. These artifacts not only reveal the mathematical knowledge possessed by the Chinese during the Shang Dynasty but also provide evidence of the earliest uses of numerical systems and calculations in Chinese history[2].The oracle bones' base 10 system was relatively simple. The first ten digits follow patterns which have mild resemblances to the current Chinese numerical characters.

Zhou Dynasty (1050 BC – 256 BC) and Warring States Period (475 BC – 221 BC)
During the Zhou Dynasty, Mathematics was required to be mastered as one of the Six Arts, a core set of Confucian philosophy. In ancient times, those who excelled in the Six Arts were revered as perfect gentlemen, embodying the highest ideals of virtue and excellence.
Yi Jing 易經 (I Ching)
The Yi Jing is translated as the "Book of Changes" is an ancient Chinese divination text that dates back to at least the Western Zhou period (around 1046 BC - 771 BC). It was often used to provide guidance for moral decision-making..
While the Yi Jing is not inherently a mathematical text, it is one of the first with mathematical elements in its structure and interpretation and greatly influenced literature during the Zhou Dynasty.
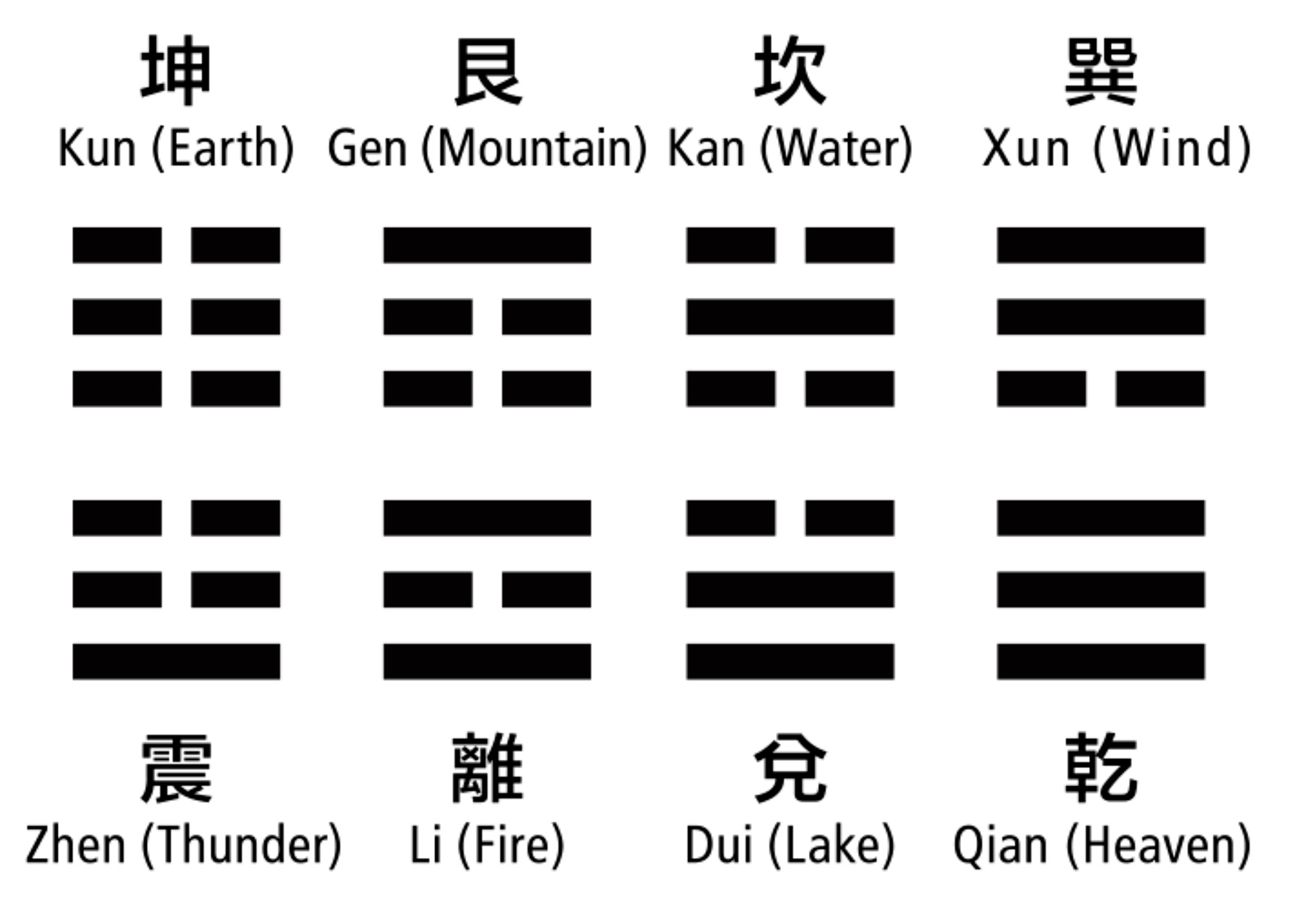
The Yi Jing is based on a binary system, which uses two fundamental elements or symbols: the solid line (Yang) and the broken line (Yin). These two lines form the basis of the trigrams and hexagrams used in the I Ching. Yin is often discussed as the female cosmic principle and Yang as the male cosmic principle[3].
Consulting the Yi Jing
These eight trigrams, known as bagua (八卦), represent a basic force of nature. Each Yi Jing hexagram consists of a combination of two trigrams. There are 64 hexagrams in total, each with its unique name, meaning, and divinatory text.
To consult the Yi Jing, the Chinese used yarrow stalks to create a hexagram. The interpretation of the readings found in the I Ching has been endlessly discussed and debated over the centuries. Qin dynasty records found that the hexagrams were privately consulted to answer questions about business, health, children and determining lucky days [4].
Counting rods
The counting board and counting rods, which emerged during the 2nd century BCE during the Warring States period, were one of the most significant mathematical innovations of that era.
The counting board was the chief computing tool, spanning from the Warring States period to 15th century AD.
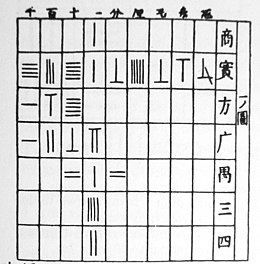
Different digits are represented by the number of rods. Counting rods were used in both vertical and horizontal formats to prevent ambiguity. There were two sets of rod notations, one for digits in odd (units, hundreds, ten thousands, etc.) positions, the other for digits in even (tens, thousands, hundred thousands, etc.) positions. These two sets were represented by vertical rods and the other represented by horizontal rods and were referred as "zongs" and "hengs" [5], respectively.
Counting rods were primarily used to calculate numbers, not record numbers like the Oracle bone script.
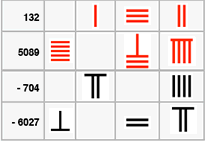
Negative numbers
Counting rods were often used for commercial and tax purposes. Red painted rods represented positive numbers and black painted rods represented negative numbers i.e the amount sold was positive and the amount spent purchasing something was negative.
Interestingly, the counting rods system spread to other parts of Asia, including Japan and Korea[6], where variations of the method were adopted and integrated into their own mathematical traditions. The lasting impact of Chinese counting rods is proof of the ingenuity of ancient mathematical systems and their ability to transcend cultural boundaries.
Qin Dynasty (221 BC – 206 BC)
There is very little evidence of mathematical advancements during the Qin dynasty, this is likely due to the short time span and also possibly because the tyrant emperor Qin Shihuangdi allegedly burned the books and buried Confucian scholars alive [7] .
Han Dynasty (206 BC – 220 AD)

Suan Shu Shu 筭數書 (Writings on Reckoning)
This text was written during the early Western Han Dynasty on some 200 bamboo strips consisting of 69 mathematical problems [8] from a variety of sources. It is one of the earliest known Chinese mathematical treatises.
A problem from the Suan Shu Shu
Problem 68:
The Li Tian Method [The Method of Measuring Farmland in Li] says: li times li are [square] li. If the width and length are both 1 li, then put [down on the counting board] 1 standing for 3, also multiply by 5 three times; the result is a field of 3 qing 75 mu. If its width and length are not equal, first multiply the [amounts of] li together, then multiply [the result] by 3, again multiply by 5, three times, which completes it [the li tian method].
[68a] Now there is a width of 220 li, and a length of 350 li, which constitute a field of 288,750 qing. To officially distribute land, use this method. [Another method] says: li multiplied by li result in [square] li. First multiply by 3 then multiply by 5 three times which is the number of qing and mu. Yet another [method] says: li times li is li. Using [li], next multiply by 25, then by 3, which also [gives] its amount [area] in qing and mu. That is to say, if the width is 1 li, and the length is 1 li, the field is 3 qing 75 mu. (Dauben, “Suan shu shu” 166-167) [9]

Jiu Zhang Suanshu 九章算衔 (The Nine Chapters on the Mathematical Art)
The Jiu Zhang Suanshu or The Nine Chapters on the Mathematical Art is one of the most significant mathematical works in Chinese history. The text focuses more on problem-solving than theory, containing 246 mathematical problems with solutions covering various practical topics such as arithmetic, geometry, algebra, and measurements.
The Nine Chapters provided methods for solving everyday problems related to engineering, surveying, trade, and taxation, making it an essential resource for practical calculations and applications at the time. It was used for centuries to train civil servants in the prestigious imperial bureaucracy. [10]
Afterward, numerous mathematicians commented on the Jiu Zhang Suanshu, with famous figures like Liu Hui (263 AD) and Li Chunfeng (656 AD) among them. Liu Hui undoubtedly was the most notable as he provided justification of the rules and explained the methods used.
All the problems take 3 as pi for calculating circles and spheres. Some mathematicians tried to approximate a more accurate value of pi for example, Liu Xin estimated pi as 3.154 but there was not even any record of how he arrived at it.
A problem from the Jiu Zhang Suanshu
Chapter 9 Problem 9:
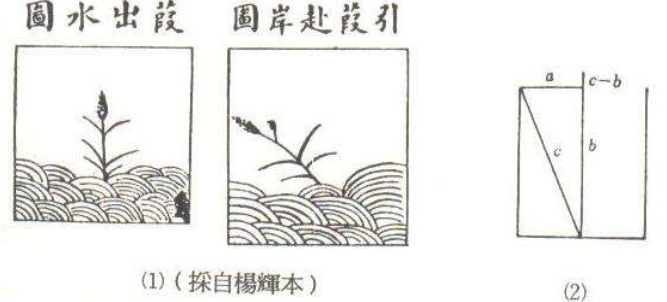
Suppose there is a [square] pond with a side of 1 zhang, in the middle of which a reed grows, extending 1 chi above the water. If the reed is pulled to the edge [of the pond], then it just reaches the edge.The question is: How much are both the depth of the water and the length of the reed?
The answer says: The depth of the water is 1 zhang 2 chi. The length of the reed is 1 zhang 3 chi.
The method says: Multiply half the side of the pond by itself.
Liu Hui commented:
"This [method] uses half the side of the pond, which gives 5 chi as the gou, the depth of the water serves as the gu, and the length of the reed is the xian. Using the gou and xian to find the gu, therefore let the gou be multiplied by itself and first find the area of the gnomon" [12]
Period of Disunity (220 AD - 589 AD)
After the Han dynasty, China's intellectual growth continued instead of slowing down. Interestingly, even when different states were at war, mathematics saw a revival. What's captivating is that during this period, people developed mathematical theories to better understand the methods explained in the texts from the earlier Han dynasty.
Liu Hui's Algorithm
Liu Hui was unsatisfied with the approximations that other mathematicians had came up with at the time, commenting that they were too large. He took an approach where he calculated the area of a polygon inscribed in a circle and as he increased the number of sides of the polygon, the area became closer to the area of the circle and using that he calculated an approximate value of π.
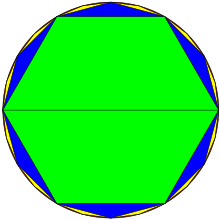
Liu Hui argued:
"Multiply one side of a hexagon by the radius (of its circumcircle), then multiply this by three, to yield the area of a dodecagon; if we cut a hexagon into a dodecagon, multiply its side by its radius, then again multiply by six, we get the area of a 24-gon; the finer we cut, the smaller the loss with respect to the area of circle, thus with further cut after cut, the area of the resulting polygon will coincide and become one with the circle; there will be no loss". [13]
His own calculation with a polygon with 96 sides yielded an accuracy of four decimal places: π ≈ 3.1416 [14].
Song Dynasty (960 AD – 1279 AD)
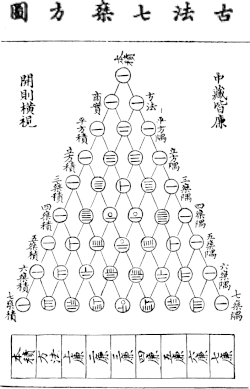
Yang Hui's triangle
This is the earliest depiction of Pascal’s triangle from Yang’s book Xiangjie Jiuzhang Suanfa 詳解九章算法 (A Detailed Analysis of the Nine Chapters on the Mathematical Art) in 1261 AD, in which he acknowledged that it was invented by mathematician Jia Xian. While the concept of this triangle had been known to different cultures before Yang Hui's time, such as Persian Mathematician Al-Karaji, he is often credited for systemising its properties and exploring its applications.
Each number in the triangle is the sum of the two directly above it, with applications in algebra, combinatorics, and probability theory. One example of its hidden properties is that each row forms the coefficients to the expansion of the binomial expression (a + b)n , where n is the row number.
Yang Hui 杨辉
Yang Hui was a Chinese mathematician and writer during the Song dynasty.
His work Xiangjie Jiuzhang Suanfa focused on the mathematical problem-solving techniques and further expanded upon the content of the "Nine Chapters on the Mathematical Art."
Around 1275 AD, Yang finally had two published mathematical books, which were known as the Xugu Zhaiqi Suanfa (續古摘奇算法) and the Suanfa Tongbian Benmo (算法通變本末) , summarily called Yang Hui Suanfa (楊輝算法).
Very little is known about Yang Hui but his works are of the few that have lasted in Chinese mathematics.
Conclusion
From the ancient roots of counting rods to advanced theorems, Chinese mathematicians have made spectacular contributions to the world of mathematics since thousands of years ago. The remarkable works of great mathematicians like Liu Hui and Yang Hui remind us of the profound impact of Chinese mathematics and how crucial diversity in mathematics is to bring fresh insights and innovative solutions.
References
1. National Museums Scotland, Oracle Bones
2. Restivo, S. (1992). The Mathematics of Survival in China. In: Mathematics in Society and History. Episteme, vol 20.
5. Bryan Clair, St Louis University - Chinese Rod Numerals
6. Frank J. Swetz (The Pennsylvania State University), "Reflections on Chinese Numeration Systems: What Are Rod Numerals?," Convergence (February 2022)
7. USC China Institute, Burning The Books And Killing The Scholars: Representing The Atrocities Of The First Emperor Of China
8. Wikipedia - Suan Shu Shu
9. Dauben, Joseph W. “算数書 Suan Shu Shu A Book on Numbers and Computations: English Translation with Commentary.” Archive for History of Exact Sciences, vol. 62, no. 2, 2008, pp. 91–178.
10. Randy Schwartz, Schoolcraft College Department of Mathematics, "A Classic from China: The Nine Chapters"
11. Rik Brandenburg, Keimpe Nevenzeel, University of Groningen, The Nine Chapters on the History of Mathematical Art
12. Guo Shuchun, Joseph W. Dauben, and Xu Yibao (2017), "Nine Chapters on the Art of Mathematics"
13. Needham.J (1959). Science and Civilisation in China, vol 3: Mathematics and the Sciences of the Heavens and the Earth
14. Wikipedia - Liu Hui's Algorithm
