How bases are used to represent numbers around the world
Using base 5, 10, and 20 is incredibly common but what is a base and how do different number systems use them?
A base is a way of splitting a number into groups of standard sizes, making it easier to describe and count. It is rather inefficient to have a different, unrelated word or symbol for each new number, so instead a base can be used to say how many of each group you have, for example, in English, the number thirty-five means there are 3 groups of ten, and five groups of 1.
Base One
Base one is the same as tallying, the number is put into groups of one. While this is an incredibly simple way of counting or recording numbers, it is very inefficient, to write the number 35 in base one, you would have to make 35 tally marks. You can read more about tallying here.
Let us explore how bases work using the Aztec base 20 system.
Aztec Numbers
Aztecs used a base 20 number system. They had 4 symbols, representing 1s, 20s, 400s, and 8000s.
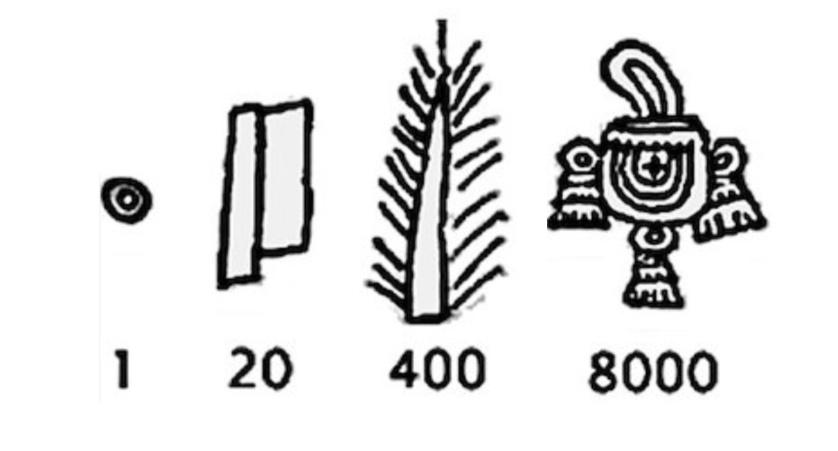
The symbol for 1 represents a maize seed, the symbol for 20 is a flag that was used to mark land boundaries, 400 is a maize plant or a feather, and 8000 is represented by what is believed to be a 'maize dolly', a figure woven from maize. [Joseph, 2011]
Because each power of 20 is represented by a different symbol, the position of the symbols does not matter. To write a number with the Aztec number system, see how many 8000s fit into that number, and write that quantity of 'maize dollies', then with the remainder see how many 400s fit into that number, and so on. For example, we write the number 10,044 as 8000 + (5x400) + (2x20) + (4x1):
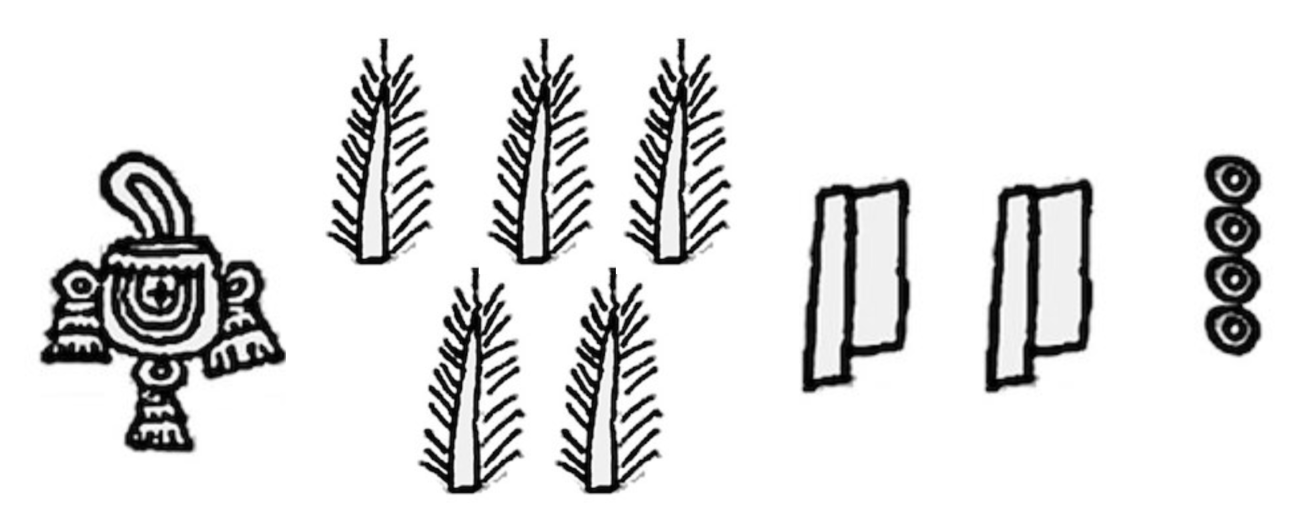
This example might seem strange because it is a mix of tallying and using base 20. In the decimal system, there is a different symbol for each number up to ten, whereas the Aztecs tallied their way up to 20 and repeated that concept for each power of 20. This is very similar to the way the Egyptians recorded numbers.
Egyptian numbers are a base 10 system but work in exactly the same way as Aztec numbers. The symbol is tallied until the next power of 10 is reached. Again, this system is non-positional so it does not matter where you draw the symbols, the value of the written number remains the same.
Bases of 5, 10, and 20 are very common all over the world and develop independently. This is down to the universal method of counting on fingers and toes, sometimes just one hand is used (base 5) or all fingers and toes are used (base 20). Some cultures do not just count on their finger and toes, for example, you can read about the Oksapmin base 27 body counting here.
Base 2 appears around the world, often in cultures where large numbers are not needed as numbers become very long and unwieldy very quickly. Here is an example of base 2 from the Gumulgal, an indigenous Australian group: [Joseph, 2011]
1 = urapon
2 = ukasar
3 = ukasar-urapon
4 = ukasar-ukasar
5 = ukasar-ukasar-urapon
6 = ukasar-ukasar-ukasar
7 = ukasar-ukasar-ukasar-urapon
We can see that already the number 7 is very long.
We have only looked at non-positional number systems that use bases, for a look at how position and order are used to represent numbers around the world, have a look at this page.

