Seasonal forcing plays a large role in the dynamics of many infectious diseases. The standard models of infection within a population predict damped oscillations tending to a fixed equilibrium value; however the constant perturbations from seasonal forcing (in conjunction with the natural damped oscillatory nature of the dynamics) can often lead to pronounced cyclic dynamics. Two particular cases of study are:

Forcing due to the opening and closing of schools.

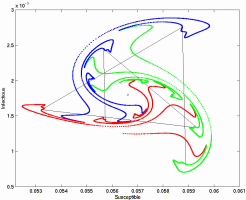For diseases such as measles or whooping-cough that display pronounced epidemic cycles, the opening and closing of schools provides the type of forcing needed to create periodic dynamics. This behaviour can be captured by including a higher rate of transmission during school terms compared with school holidays. We are interested in four main questions:

1) Can the deterministic dynamics be captured by thinking about discrete switching between term-time and holiday-time orbits? (see Figure)

2) How do the deterministic dynamics and stochastic behaviour interact to produce the observed pattern of epidemics in the UK and elsewhere?

3) How does age-structure and the fact that only children go to school affect the dynamics?

4) Can these concepts be extended to other childhood diseases, using the parameters for measles and pertussis as a template?

 

Forcing due to birth pulses.

Many animals give birth during a short breeding season. This means that the population dynamics of the host undergoes significant seasonal fluctations, we wish to assess the impact of these fluctations on infectious diseases.

The simplest model assumes that all births occur as an instantaneous pulse once per year -- thus applying a large perturbation to the dynamics. Although not analytically tractable, this model is ameanable to detailed numerical investigation. A number of interesting conclusions have been reached:

1. The model can give rise to co-existing multi-annual periodic cycles.
2. The existance and position of these cycles in parameter space is largely unaffected if wider birth pulses are assumed
3. This is an extreme example of non-linear resonance.

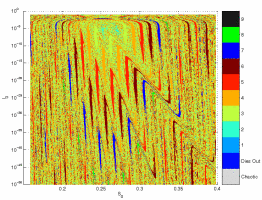
The figure shows the basin of attraction for one set of parameter values. For each set of initial conditions (starting proportion of susceptibles (x-axis) and starting proportion of infecteds (y-axis)) the point is colour-coded to indicate the period of the long-term dynamics.

 

Publications

MJ Keeling, P Rohani, BT Grenfell (2001). Seasonally-forced Disease Dynamics Explored as Switching Between Attractors. Physcia D 148, 317-335.

P Rohani, MJ Keeling, BT Grenfell (2002). The Interplay Between Determinism and Stochasticity in Childhood Diseases. Am. Nat. 159, 469-481.