Immunology
There are two major fields of mathematical modelling of infectious diseases: mathematical epidemiology and mathematical immunology. In mathematical epidemiology, the spread of disease in a population of hosts is studied with the goal of tracing factors that contribute to the propagation of the pathogen. Mathematical immunology is concerned with the study of disease dynamics within an infected host. The aim is to determine the underlying mechanisms of disease progression by focusing on the interactions between the pathogen and the immune system.
We are interested in developing within-host models of pathogen dynamics that enable us to obtain a greater understanding of the key mechanisms that allow a pathogen to persist both within the host and within the population. Such models serve to predict vaccines and drug therapies that should be implemented to best aid the immune system in fighting invading pathogen, and may offer key insights into evolutionary contraints.
Our goal is to ultimately develop an integrated epidemiological framework that is built upon a foundation of immunological modelling rather than the usual compartmental descriptions usually applied to describe the status of a host. Detailed immunological input will be key to the success of this long-term project.
Waning Immunity
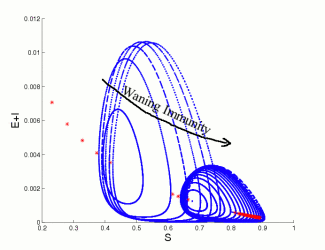Vaccine waning involves the loss of immune system memory cells (T-cells) that pertain to a particular illness. For infectious diseases where immunization can offer life-long protection, a variety of simple models can be used to explain the utility of vaccination as a control method. However, for many diseases immunity wanes over time and is subsequently enhanced (boosted) by asymtomatic encounters with the infection. To study this type of epidemiological process requires a model formulation that can capture both the within-host dynamics of the pathogen and immune system as well as the associated population-level transmission dynamics. We have developed and parameterised such a model for measles, and to show how vaccination can have unexpected consequences as it reduces the natural boosting of immunity. In particular we've shown that relatively short waning times (10-30 years) and high levels of vaccination (greater than 70\%) can induce large-scale oscillations with substantial numbers of cases being generated at the peak. In addition, we predict that after a long disease-free period introduction of infection will lead to far larger epidemics than predicted by standard models. These results have clear implications for the long-term success of any vaccination campaign and highlights the need for a sound understanding of the immunological mechanisms of immunity and vaccination.
HIV
Immunological models are well suited to HIV/AIDS studies because of the complex interplay between viral evolution and the immune system dynamics of hosts. My PhD research centred around the development of in-hosts models of HIV that incorporate stochasticity and biologically motivated lifetime distributions for the cells and virions in the system. Using a Monte Carlo simulation I quantified the expected variation in HIV infection in-host and determined the probability of viral clearance under a number of different assumptions i.e. changes in the underlying lifetime distributions of the cells and virions in the system, an increasing bud rate of virions, the inclusion of accurate pharmacokinetics and the inclusion of more than one viral strain (in which different mutant strains confer different levels of resistance to the drugs in the system). This work is complementary to conventional models of HIV infection which are deterministic and thus cannot predict the variance in infection nor the probability of viral extinction. The results from my stochastic model also have clinical applications as the model can be used to predict the magnitude of changes in viral load that are not clinically significant.
Influenza
The immune system plays an important role in the evolution and progression of influenza. Here, I am interested in developing a within-host model of pathogen evolution with the aim of paramaterizing epidemiological models of influenza such that they are more sensitive to changes in transmission rates, the length of the infectious period and the degree of virulence. Influenza is expected to be strongly affected by within-host evolution as it is an acute infection with relatively fast mutation rates. It is also likely that such a model for influenza could be used to model other viruses of a similar type (such as Foot and Mouth Disease) with minimal adjustment.
