Many mathematical models of ecological and epidemiological populations are deterministic. This means they are essentially fixed “clockwork” systems; given the same starting conditions, exactly the same trajectory is always observed. Such a Newtonian view of the world does not apply to the dynamics of real populations. For example, if it were possible to “re-run” a real-world epidemic, we would not expect to observe exactly the same people becoming infected at exactly the same times. Clearly, there is an important element of chance. Stochastic models are concerned with approximating or mimicking this random or probabilistic element.

Stochasticity occurs from two basic sources; (i) demographic stochasticity due to the random nature of events and the individuality of populations, and (ii) environmental stochasticity due to the irregular or noisy dynamics of some process outside the biological system (such as the weather). Much of my research concentrates exclusively on the well defined notion of demographic stochasticity, although in reality both processes are usually present. Research is focussed towards understanding how stochasticity influences population dynamics and how these differences can be captured without the need for large-scale stochastic simulations.

When does stochasticity matter?

In general, the role played by stochasticity will be most important whenever the number of infectious individuals is relatively small, which can be when the population size is small, when an infectious disease has just invaded, when control measures are successfully applied, or during the trough phase of an epidemic cycle. In such circumstances, it is especially important that stochasticity is taken into account and incorporated into models. Stochasticity has three main effects that are of practical interest:

1. it drives fluctuations in disease insidence,
2. it leads to increased transcient dynamics and stochastic resonance,
3. it can cause chance extinction of an infection.
   

Research is focused towards how these elements can explain observed patterns of case reports and how they can be exploited to better control infection. A good example is how to maximise chance extinctions and minimise re-invasion of infection in a population -- can this be achieved by heterogeneous deploitment of vaccination?

Moment closure approaches.

Moment closure is a technique by which higher order moments are approximated in terms of lower order ones, such that a closed system of equations can be developed. Moment closure for stochastic models is to consider distributions of population sizes, and in general we formulate equations for means, variances and covariances and then approximate the third order cumulates (the skew) in terms of the known variables (means & variances). Such models allow us to extend standard deterministic models so as to approximate the amount of variance that occurs due to the presence of demographic stochasticity or environmental noise. I have applied this theory to two different situations,

1) For an infinite set of habitats with rapid global movement of individuals (a metapopulation) it is obvious that the population distributions should be close to Poisson. The moment-closure technique allowed us to relax this rapid mixing limit, and hence consider the stability of natural enemy systems (the Lotka-Volterra and Nicholson-Bailey models) as heterogeneities begin to develop. This work showed that heterogeneities could be either stabilising or destabilising, and that there were significant differences between the two models studied.

2) The technique was extended further by considering a small number of subpopulations, such that there is variance at both the habitat and meta-population scale. For these models, the closure technique assumed that the distributions were close to log-normals. In this way the extinction risk of a variety of models could be theoretically calculated; single species models persisted best when movement between patches was large, whereas natural-enemy models persisted best for intermediate levels of coupling.

We believe that moment-closure techniques will become increasingly important in understanding biological phenomenon, as the roles played by stochasticity and individuals receive more recognition.

Kolmogorov forward equations.

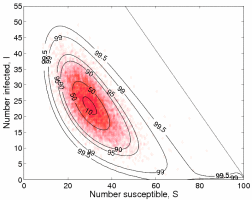Models which deal with the individual nature of populations have shown the importance of stochasticity in ecology, epidemiology and evolution. An increasingly common approach to studying these models is through stochastic (event-driven) simulation. One striking disadvantage of this approach is the need for a large number of replicates to determine the range of expected behaviour. Often, these models can be reformulated in term of the so-called Kolmogorov-forward equation (also called Ensemble or Master equation) which simultaneously consider the probability
of each possible state occurring. Irrespective of the complexities and non-linearities of population dynamics, this equation is linear and has a natural matrix formulation which provides many analytical insights into the behaviour of stochastic populations and allows rapid evaluation of process dynamics. We have generally concentrated on using this approach for epidemiological models due to the simple nature of the possible stochastic events.

The graph on the right shows a comparison between the long-term equilibrium distribution as predicted by the Kolmogorov-forward equations (lines - determined by the dominant eigenvalue of the transition matrix) and the results of a demograph (event-driven) stochastic model (red dots). As expected these results are in clear agreement; however it should be noted that theKolmogorov-forward equations can provide exact answers for the distribution, capturing the occurance of very rare events.

 

Publications

P Rohani, O Miramontes, MJ Keeling (2004). The colour of noise in short ecological time series data. Math Med & Biol 21, 63-72.

MJ Keeling, BT Grenfell (2002). Understanding the Persistence of Measles: Reconciling Theory, Simulation and Observation. Proc. Roy. Soc. Lond. B 269, 335-343.

MJ Keeling, HB Wilson, SW Pacala (2002). Deterministic limits to stochastic, spatial models of natural enemies. Am. Nat. 159, 57-80.

MJ Keeling (2000) Multiplicative Moments and Measures of Persistence in Ecology J. Theor. Biol. 205, 269-281

MJ Keeling (2000) Simple Stochastic Models and their Power-law Type Behaviour Theo. Pop. Biol. 58 21-31

MJ Keeling (2000) Metapopulation moments: coupling, stochasticity and persistence J. Animal Ecology 69 725-736

MJ Keeling, HB Wilson and SW Pacala (2000) Re-interpreting Space, Time-lags and Functional Responses in Ecological Models Science 290 1758-1761

MJ Keeling and BT Grenfell (1999) Stochastic Dynamics and a power law for measles variability Phil. Trans. Roy. Soc. Lond. B 354 769-776

MJ Keeling and BT Grenfell (1997) Disease Extinction and Community Size: Modeling the Persistence of Measles Science 275 65-67

MJ Keeling and BT Grenfell (1997) Impact of Variability in Infection Period on the Persistence and Spatial Spread of Infectious Diseases Math BioSciences 147 206-227