The AGATA seminar is a new seminar at Warwick for young researchers in Algebraic Geometry, Algebraic Topology and Algebra.

If you would like to suggest a speaker or have any inquiries, please contact one of the organisers: Diego (Algebra), David (Algebraic Geometry) or Julie (Algebraic Topology).

Term 3

During term 3, the seminar will take place Thursdays at 5 pm in MS.05.

Date	Speaker	Affiliation	Title
May 11	Pavel Turek	Royal Holloway, University of London	Multiplicity-free induced characters of symmetric groups
May 18	Rhiannon Savage	University of Oxford	Derived Geometry Relative to Monoidal Quasi-abelian Categories
May 25
Jun 1	Matthew Chaffe	University of Birmingham	Modular Representation Theory of truncated current Lie algebras
Jun 8
Jun 15
Jun 22
Jun 29	Erroxe Etxabarri Alberdi	University of Nottingham

Abstracts

Pavel Turek: Multiplicity-free induced characters of symmetric groups

Let $n$ be a sufficiently large positive integer. Wildon and independently Godsil and Meagher have found all subgroups $G$ of the symmetric group $S_n$ such that when the trivial character of $G$ is induced to $S_n$ we obtain a multiplicity-free character. In this talk we focus on a more general problem when the trivial character of $G$ is replaced by an arbitrary irreducible character of $G$. After introducing the necessary background I present some of the group theoretic and combinatorial techniques and results such as the Littlewood-Richardson rule used to study this problem. In the final part of this talk I show some of my (often surprising) results such as the full classification of subgroups $G$ of $S_n$ such that there is an irreducible character of $G$ which stays multiplicity-free when induced to $S_n$.

Rhiannon Savage: Derived Geometry Relative to Monoidal Quasi-abelian Categories

In the theory of relative algebraic geometry, we work with respect to a symmetric monoidal category C. The affines are now objects in the opposite category of commutative algebra objects in C. The derived setting is obtained by working with a symmetric monoidal model or -category C, with derived algebraic geometry corresponding to the case when we take C to be the category of simplicial modules over a simplicial commutative ring k. Kremnizer et al. propose that derived analytic geometry can be recovered when we instead use complete bornological rings. We can provide an overarching theory by working with commutative algebra objects in certain quasi-abelian categories. In this talk, I will introduce these ideas and briefly discuss how we can obtain interesting results, such as a representability theorem for derived stacks in this context.

Matthew Chaffe: Modular Representation Theory of truncated current Lie algebras

In this talk I will discuss the representation theory of truncated current Lie algebras in prime characteristic. I will first give an introduction to modular representation theory for general restricted Lie algebras and introduce the Kac-Weisfeiler conjectures. Then I will discuss the specific case of truncated current Lie algebras and relationships with the representation theory of reductive Lie algebras.

Term 2

Date	Speaker	Affiliation	Title
Feb 16	Samuel Muñoz Echániz	University of Cambridge	Mapping class groups of h-cobordant manifolds
Feb 23	Alberto Cobos Rábano	University of Sheffield	The landscape of Enumerative Geometry
Mar 02	Adele Jackson	University of Oxford	Algorithms and 3-manifolds
Mar 09	James Timmins	University of Oxford	Dimensions in noncommutative algebra
Mar 16	Javier Aguilar Martin	University of Kent	Introduction to derived -algebras

Abstracts

Samuel Muñoz Echániz: Mapping class groups of h-cobordant manifolds

Given two h-cobordant manifolds L and M, how much do (the homotopy types of) the diffeomorphism groups Diff(L) and Diff(M) differ? We will see that the homotopy groups of these two spaces are the same “up to extensions” in positive degrees in a range. Contrasting this fact, I will present an example of h-cobordant manifolds with different mapping class groups. In doing so, we will review the basics of simple homotopy theory and introduce several moduli spaces of manifolds analogous to classifying spaces of diffeomorphism groups.

Alberto Cobos Rábano: The landscape of Enumerative Geometry

I will present some of the tools and techniques used in Enumerative Geometry, which is the field of Algebraic Geometry concerned with counting solutions to geometric problems. One such problem is to determine the number of degree-d curves through 3d-1 points (in general position) in the projective plane. More generally, we will focus on the number of curves intersecting certain subvarieties in the projective space P^r. These numbers are called the Gromov-Witten invariants of P^r. Time permitting, I will present some of the latest developments in reduced Gromov-Witten invariants, which is work in progress with Etienne Mann, Cristina Manolache and Renata Picciotto.

Adele Jackson: Algorithms and 3-manifolds

Given a mathematical object, what can you compute about it? In some settings, you cannot say very much. Given an arbitrary group presentation, for example, there is no procedure to decide whether the group is trivial. In 3-manifolds, however, algorithms are a fruitful and active area of study (and some of them are even implementable!). One of the main tools in this area is normal surface theory, which allows us to describe interesting surfaces in a 3-manifold with respect to an arbitrary triangulation. I will discuss some results in this area, particularly around Seifert fibered spaces.

James Timmins: Dimensions in noncommutative algebra

Due to the dictionary between commutative algebra and algebraic geometry, the size of commutative algebras and their modules can be measured by the dimension of geometric objects. In this talk, I’ll describe the picture for noncommutative algebra, focusing on a fundamental invariant known as canonical dimension. I’ll illustrate the theory with a classical example that leads to Bernstein’s inequality, and then describe recent progress for completed group algebras of p-adic groups, giving a connection to the (mod p) Langlands programme.

Javier Aguilar Martin: Introduction to derived 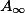-algebras

We introduce the notion of homotopy associative (-) algebras in the framework of operads, with loop spaces as our main example. We will motivate the study of these algebraic structures through the theory of minimal models. We will also see their interaction with brace algebras coming from operadic structures. Derived -algebras will be introduced to overcome the limitations of classical -algebras.