Finite metric graphs are used as a tool in many areas of science and mathematics, ranging from phylogenetic trees in biology to scattering amplitudes in physics to degenerations of Riemann surfaces in mathematics. This gives strong motivation for understanding the structure of the space of all such graphs. Karen Vogtmann'sLink opens in a new window work with physicist Michael BorinskyLink opens in a new window on understanding spaces of graphs was recently profiled in Quanta magazine: ``Quantum field theory pries open Mathematical PuzzleLink opens in a new window". The puzzle referred to in that article is in fact just a piece of a much larger puzzle, that of understanding the space – the space of all possible finite connected metric graphs with Euler characteristic equal to 1-n.

An important invariant of a topological space is its cohomology. This is a sequence of abelian groups, where the k-th group is sometimes described as measuring how many ``k-dimensional holes" the space has. The cohomology of the space is still very mysterious. In particular, the cohomology has not been computed beyond n=7. An invariant which is usually easier to compute is the Euler characteristic; this is the alternating sum of the ranks of the cohomology groups. The Euler characteristic can yield key information, such as bounds on cohomology. In 1987, Vogtmann and John SmillieLink opens in a new window found a generating function for a close relative of the Euler characteristic of called the orbifold Euler characteristic. This generating function made it possible to compute the value of the orbifold Euler characteristic for any given n, assuming one could find a large enough and fast enough computer. However, it was not possible to extract qualitative information from this generating function, such as how fast the orbifold Euler characteristic was growing or even whether it was always non-zero. Furthermore, the orbifold Euler characteristic, though interesting in its own right and closely related to the actual Euler characteristic, is not equal to it. The actual Euler characteristic is generally much more difficult to compute.

These questions about the Euler characteristic seemed intractable until a chance encounter at a conference on perturbative quantum field theory where Vogtman attended Borinsky's talk on counting Feynman diagrams. Vogtmann and Borinsky began a collaboration resulting in two papers that answer all of the above questions about the Euler characteristic of . The first paper concentrates on the orbifold Euler characteristic, showing it is always negative (in particular non-zero) and determining its asymptotic growth rate. This was done by producing a sort of ``inverted Stirling's formulaLink opens in a new window", whose coefficients encoded the rational Euler characteristic. This asymptotic expansion was then compared with another asymptotic expansion for the same function in the same scale, derived from a known asymptotic expansion of the Lambert W-functionLink opens in a new window. Since two asymptotic expansions of the same function in the same scale have the same coefficients, it was possible to extract the needed information. The second paper builds on these results, also employing a prior theorem of Ken BrownLink opens in a new window relating the orbifold Euler characteristic to the usual Euler characteristic and previous work by Vogtmann and Sava KrsticLink opens in a new window. In the end, Vogtmann and Borinsky have been able to determine the asymptotic growth rate of the actual Euler characteristic of .

The results are striking. The Euler characteristic is negative when n is large enough and grows extremely fast. This indicates that there is a huge amount of odd-dimensional cohomology ...., and yet only one odd-dimensional class has ever been found, by Laurent BartoldiLink opens in a new window in 2015 using a mind-boggling amount of CPU time on a computer!

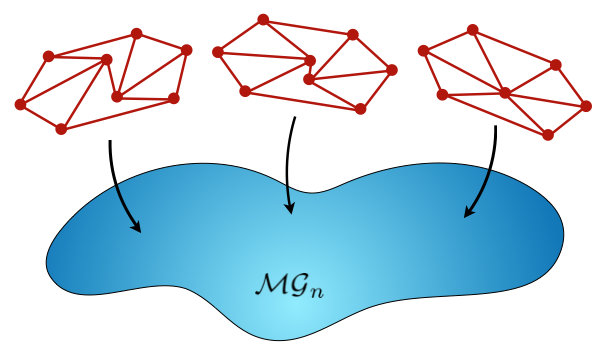
Illustration of the space of all finite connected metric graphs with Euler characteristic equal to 1-n. Each point in the space corresponds to a metric graph, and you move around the space by varying the lengths of the graph's edges. A set of edges can shrink to points as long as they do not contain a loop, so that shrinking edges changes the combinatorial structure of the graph, but not its Euler characteristic.

The goal is to understand the topological structure of spaces for different n, particularly n large.

Question for the reader: three graphs in the space are illustrated above. What is the value of n in the case illustrated?

Bonus question: Draw three graphs in the space .

Further reading:

• The Euler characteristic of Out(F_n)Link opens in a new window, by Borinsky & Vogtmann.
• Computing Euler characteristics using quantum field theoryLink opens in a new window, by Borinsky & Vogtmann.
• The Euler characteristic of the moduli space of graphsLink opens in a new window, by Borinsky & Vogtmann.
• Hearing Euler characteristic of graphsLink opens in a new window, by Ławniczak et al.