News 2014
- 2014
-
Pumpkin Geometry - Guardian article about Saul Schleimer and Henry Segerman (30th October 2014)
Dan Kral and David Loeffler win Philip Leverhulme Prizes (30th October 2014)
Martin Hairer wins a Fields Medal (13th August 2014)
Mark Pollicott awarded EPSRC Fellowship (6th August 2014) - Professor Nigel Hitchin FRS receives honorary degree (28th July 2014)
- WIDER's work on bovine TB in the news (26th July 2014)
- Karen Vogtmann wins the Humboldt Research Prize (16th July 2014)
- Four Mathematics graduates win Faculty prizes for their PhDs (5th July 2014)
- Three Warwick Mathematicians win senior LMS prizes (4th July 2014)
- Warwick Mathematics 4th in Guardian 2015 table (10th June 2014)
- Oleg Zaboronski awarded Leverhulme Research Fellowship (13th May 2014)
- Karen Vogtmann wins a Royal Society Wolfson Research Merit award (9th May 2014)
- Martin Hairer elected Fellow of the Royal Society (1st May 2014)
-
Martin Hairer appointed Regius Professor (30th April 2014)
Sandy Green passed away (17th April 2014) - Robert MacKay named EPSRC RISE Renowned Fellow (11th April 2014)
- Filip Rindler awarded EPSRC Fellowship (24th February 2014)
- Martin Hairer & José Luis Rodrigo win ERC Consolidator grants (4th February 2014)
- 2013
30th October 2014
Pumpkin Geometry - Guardian article about Saul Schleimer and Henry Segerman
On October 30th the work of Saul Schleimer and Henry Segerman was featured in an on-line article in the Guardian, written by Alex Bellos. The title of the article, "Pumpkin geometry", combines a seasonal reference, to Halloween, and a mathematical reference to the concept of stereographic projection. In a sequence of 3D prints Schleimer and Segerman show how to use stereographic projection, via light and shadow, to transform spherical geometry (the "pumpkin") into euclidean and hyperbolic geometry.
Photo Courtesy of Henry Segerman
The article can be found here.
30th October 2014
Dan Kral and David Loeffler win Philip Leverhulme Prizes
Philip Leverhulme Prizes are awarded to outstanding scholars who have made a substantial and recognised contribution to their particular field of study, recognised at an international level, and where the expectation is that their greatest achievement is yet to come. 5 prizes are awarded in Mathematics and Statistics every 2 years.
Dan Král's work during his fellowship will focus on combinatorial limits. The theory of combinatorial limits is a recently emerged and rapidly evolving area of mathematics, which led to opening new links between analysis, combinatorics, computer science, group theory and probability theory.
The analytic view of large discrete structures resulted in a substantial progress on many notoriously difficult extremal combinatorics questions. It also gave new understanding of aspects of important concepts such as regularity decompositions. Still, many fundamental problems remain widely open. A particularly challenging problem is finding a robust notion of convergence that would unify the existing notions for dense and sparse discrete structures. In relation to extremal combinatorics, problems of a great significance include a full description of low dimensional projections of the body of feasible limit densities or the existence of finitely forcible (determined) configurations in the extremal points of this body as conjectured by Lovász and Szegedy.
David Loeffler received a joint award with his wife Sarah Zerbes (UCL) for their work on Euler systems. Euler systems are sophisticated mathematical tools used to study problems in number theory - perhaps the oldest branch of mathematics, but also one of the richest and most active areas of current research. Number theorists are interested in properties of the integers (whole numbers, as opposed to fractions or irrational numbers), such as factorizing numbers into primes, or finding solutions to equations where the unknowns are whole numbers.
Loeffler and Zerbes' work is closely related to one of the most important unsolved problems in pure mathematics, the Birch—Swinnerton-Dyer conjecture, which concerns a special class of equations called "elliptic curves". The BSD conjecture predicts that the existence of solutions to such equations is closely related to the behaviour of certain complex-analytic functions called "L-functions".
The Euler system that they have constructed gives a way to relate the L-function back to the arithmetic of the underlying elliptic curve, bringing new cases of the BSD conjecture within reach. In ongoing research they plan to extend this construction from elliptic curves to more general classes of equations, such as Abelian surfaces.
List of 2014 Philip Leverhulme Prize winners
13th August 2014
Martin Hairer wins a Fields Medal 2014
At the opening ceremony of the International Congress of Mathematicians 2014 on August 13, 2014 in Seoul, Korea, a Fields Medal was awarded to Professor Martin Hairer FRS for his outstanding contributions to the theory of stochastic partial differential equations, and in particular for the creation of a theory of regularity structures for such equations. Martin has worked in Warwick since 2002, and in April 2014 was appointed to the Department's new Regius Professorship.
Short citation: A mathematical problem that is important throughout science is to understand the influence of noise on differential equations, and on the long time behavior of the solutions. This problem was solved for ordinary differential equations by Itô in the 1940s. For partial differential equations, a comprehensive theory has proved to be more elusive, and only particular cases (linear equations, tame nonlinearities, etc.) had been treated satisfactorily.
Hairer’s work addresses two central aspects of the theory. Together with Mattingly he employed the Malliavin calculus along with new methods to establish the ergodicity of the two-dimensional stochastic Navier–Stokes equation.
Building on the rough-path approach of Lyons for stochastic ordinary differential equations, Hairer then created an abstract theory of regularity structures for stochastic partial differential equations (SPDEs). This allows Taylor-like expansions around any point in space and time. The new theory allowed him to construct systematically solutions to singular non-linear SPDEs as fixed points of a renormalization procedure.Hairer was thus able to give, for the first time, a rigorous intrinsic meaning to many SPDEs arising in physics.
Press release (PDF)
List of 2014 prizewinners
Quanta magazine article
Video of Martin Hairer's work
Fields Medal Presentation
Photo Courtesy of Mark Pollicott
6th August 2014
Mark Pollicott awarded EPSRC Fellowship
Professor Mark Pollicott has been awarded a 5-year EPSRC Leadership Fellowship for his proposal: '' Applications of ergodic theory to geometry''. An element of the £934k support will be support for 2 three year postdocs.
The proposed research lies at the interface of Ergodic Theory and Dynamical Systems, geometry, number theory, partial differential operators and mathematical physics. Central to this research programme are the the application of ideas from smooth ergodic theory to problems in different areas of mathematics.
A key idea is the development of the theory of dynamical zeta functions. The most familiar zeta function in mathematics is the Riemann zeta function, which is used to study prime numbers. Dynamical zeta functions are defined analogously, where prime numbers are replaced by closed orbits of hyperbolic (or chaotic) dynamical systems as the main objects of interest.
Links:
Proposal title and details
28th July 2014
Professor Nigel Hitchin FRS receives honorary degree
On Friday 18th July, Professor Nigel Hitchin FRS was awarded an Honorary Doctorate of Science.
Nigel Hitchin is one of the world's foremost geometers. His work occupies a unique place on the frontier between differential and algebraic geometry and mathematical physics. His influence has been enormous, his remarkable succession of highly original scientific work being widely cited across many different branches of mathematics.
Professor Hitchin held a chair at the Warwick University Mathematics Department 1990-1994, during which time he was elected a Fellow of the Royal Society.
The full text of the oration by Professor Caroline Series can be found here
26th July 2014
WIDER's work on bovine TB in the news
The publication earlier this month in Nature by Ellen Brooks Pollock (Cambridge), Gareth Roberts (Statistics) and Matt Keeling (Mathematics and Life Sciences) of their joint paper has stirred up a great deal of interest not just in the scientific community but also the daily newspapers and BBC TV news.
This work was begun in 2008 and follows on from other successful research at Warwick and Cambridge on both bovine TB and modelling livestock infections. This is the first time that anyone has developed a mechanistic mathematical national-scale model for the spread of bovine TB that accounts for multiple routes of transmission and allows the impact of different controls to be tested.
Their model shows that transmission is complex and multifaceted – with cattle-to-cattle transmission, failure to detect infection, movement of infected animals and transmission from the environment all playing a role. The authors believe it is this complexity that continues to fuel scientific and public debate about bovine TB.
Links:
Nature article: A dynamic model of bovine tuberculosis spread and control in Great Britain
WIDER news
16th July 2014
Karen Vogtmann wins the Humboldt Research Prize
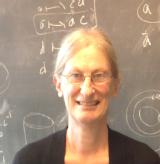On Thursday 3rd June Professor Karen Vogtmann was awarded a Humboldt-Forschungspreis (Humboldt Research Award) from the Alexander von Humboldt Foundation in Germany.
The award is granted in recognition of a researcher's lifetime achievements to academics whose fundamental discoveries, new theories, or insights have had a significant impact on their own discipline and who are expected to continue producing cutting-edge achievements in the future. Vogtmann was cited as an internationally renowned leader in the rapidly growing field of geometric group theory, who has made important contributions to our understanding of the automorphism groups of free groups. The introduction of what came to be known as Culler–Vogtmann space or “outer space” opened the way for a geometric study of these groups and their homology. In Germany, she will investigate combinatorial boundaries for outer space as well as instances of the Farrell–Jones conjecture.
Links:
Humboldt Foundation
Wikipedia article on the Humboldt Prize
5th July 2014
Four Mathematics graduates win prizes for their PhDs
The Faculty of Science has inaugurated prizes for the best PhD theses in each of the science departments. The four winners in the Mathematics Institute for 2013 are:
- David Bate: Structure of Measures in Lipschitz Differentiability Spaces
- Gareth Speight: Porosity and Differentiability
- Robert Tang: Covering Maps and Hulls in the Curve Complex
- Sebastian Vollmer: Efficient MCMC and Posterior Consistency for Bayesian Inverse Problems
4th July 2014
Three Warwick Mathematicians win LMS prizes
Three Warwick mathematicians have been awarded prestigious prizes for their work by the London Mathematical Society (LMS).
Professor Miles Reid FRS is awarded a PÓLYA PRIZE for his exceptionally creative work on higher dimensional algebraic geometry; in particular, on canonical singularities, the MacKay correspondence, the explicit study of 3-dimensional flips, the structure of Gorenstein rings, and for his inspired expositions.
From the citation: Miles Reid has done fundamental work on surfaces of general type with low invariants; he invented terminal and canonical singularities, in work that revolutionised the field of higher dimensional algebraic geometry; he extended the McKay correspondence to higher dimensions; he is making pioneering discoveries in the structure theory of Gorenstein rings in codimension 4 and higher; he is advancing a monumental project of classification of 3-fold flips. In his research work, Reid has often been a pioneer, often years ahead of his time.
Professor Martin Hairer FRS is awarded a FRÖHLICH PRIZE for his work on the interface between probability theory and partial differential equations.
From the citation: Martin Hairer’s recent research is regarded as having revolutionized an entire field of research lying between probability theory and partial differential equations. His theory of regularity structures provides a mathematical framework in which it is possible to formulate and understand a number of equations describing the temporal evolutions of certain random systems exhibiting large-scale fluctuations. In particular, it gives a solution theory for the KPZ equation and for the dynamical $\Phi^4_3$ model.
Professor Caroline Series is awarded a SENIOR ANNE BENNETT PRIZE in recognition of her leading contributions to hyperbolic geometry and symbolic dynamics, and of the major impact of her numerous initiatives towards the advancement of women in mathematics. Caroline Series is the first winner of the SENIOR ANNE BENNETT PRIZE which is awarded in memory of Anne Bennett, a gifted scientific administrator who died suddenly whilst working for the Society.
Caroline Series’ research concerns intricate and fundamental questions about the geometry of surfaces and 3-manifolds. Besides groundbreaking research, her wide ranging contributions to the community of mathematicians include a distinguished record of relentless effort in encouraging women mathematicians, both as a founder member of European Women in Mathematics and in many subsequent initiatives.
10th June 2014
Warwick Mathematics 4th in Guardian 2015 table
The University of Warwick's Mathematics Department was placed 4th in the Guardian league table for mathematics for the 2015 entry.
The Guardian table ranks departments based on factors related to the choice of degree course for incoming students such as student satisfaction with the course and the teaching, student/staff ratios and employment within 6 months of a successful completion of a degree course.
13th May 2014
Oleg Zaboronski awarded Leverhulme Research Fellowship
Associate Professor Oleg Zaboronski has been awarded a Leverhulme Research Fellowship for 2014–15 to investigate Eigenvalue processes for matrix-valued Brownian motions.
Exactly solvable agent-based (particle) models are of great interest in physics, biology and economics. For many such models, the statistical behaviour is universal and described by large random matrices. There is evidence that a fundamental particle system (Brownian particles killing each other or coagulating on contact) is also related to random matrices (populated with independent Brownian motions). The aim of the proposed research is to pin this relation down and generalize to more elaborate particle systems. Reaching this aim requires solution to a long-standing problem of dynamic correlations in random matrix theory thus advancing our understanding of stochastic processes associated with random matrices.
9th May 2014
Karen Vogtmann wins a Royal Society Wolfson Research Merit award
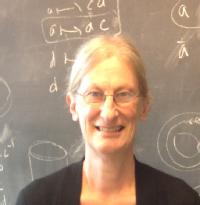Professor Karen Vogtmann has been awarded a prestigious Royal Society Wolfson Research Fellowship for 2014–15 to investigate “Outer spaces in geometric group theory”.
Groups are algebraic objects that encode symmetry, which explains why they are fundamental to all of mathematics and the physical sciences. Groups themselves have symmetries called automorphisms, and the simplest groups often have the most complex and interesting autoorphism groups. Professor Vogtmann works on developing geometric tools for studying such automorphism groups. This specific project concentrates on outer automorphism groups of free groups and more generally of right-angled Artin groups, a class of groups particularly relevant to recent breakthroughs in 3-manifold topology.
The awards, which are administered by the Royal Society, are jointly funded by the Wolfson Foundation and the Department for Business, Innovation and Skills (BIS); the scheme aims to provide universities with additional support to enable them to attract science talent from overseas and to retain respected UK scientists of outstanding achievement and potential.
1st May 2014
Martin Hairer elected Fellow of the Royal Society
Martin Hairer, Regius Professor of Mathematics, has been elected a Fellow of the Royal Society.
Professor Martin Hairer is one of the world's foremost leaders in the field of stochastic partial differential equations in particular, and in stochastic analysis and stochastic dynamics in general. By bringing new ideas to the subject he made fundamental advances in many important directions such as the study of variants of Hormander's theorem, systematisation of the construction of Lyapunov functions for stochastic systems, development of a general theory of ergodicity for non-Markovian systems, multiscale analysis techniques, theory of homogenisation, theory of path sampling and, most recently, theory of rough paths and the newly introduced theory of regularity structures.
30th April 2014
Martin Hairer appointed Regius Professor
Martin Hairer has been appointed as the Warwick Mathematics Institute's first ever Regius Professorship following the award to the Mathematics Institute of a prestigious Regius Professorship by the Queen to mark her Diamond Jubilee.
11th April 2014
Robert MacKay named RISE Renowned Fellow
Robert MacKay is one of three Fellows of the Royal Society at Warwick who have been named RISE Renowned Fellows after nomination for the EPSRC RISE Awards (Recognising Inspirational Scientists and Engineers).
The RISE campaign, in partnership with the Royal Academy of Engineering, marks the 20th anniversary of the EPSRC. Ten of the UK’s most inspirational scientists and engineers have been recognised as RISE Leaders, celebrating their achievements as innovators in engineering and physical sciences research. Their contribution to science covers a broad range of disciplines and highlights the diversity and impact of the engineering and physical sciences.
Philip Greenish, CBE, Chief Executive of the Royal Academy of Engineering commented:
“RISE is part of the Engineering for Growth campaign which aims to bring engineering to the heart of society; celebrating the contribution of inspiring researchers to growth and innovation is a great way to help create a connection between engineering and daily life.”
24th February 2014
Filip Rindler awarded EPSRC Fellowship
Filip Rindler, a Warwick Zeeman Lecturer, has been awarded a 3-year EPSRC Fellowship to investigate Singularities in Nonlinear PDEs which is to start in October 2014 and which includes funding for a related workshop.
This project aims to further the theoretical understanding of singularities, manifested as oscillations and concentrations, in solutions to nonlinear partial differential equations. Since such singularities are not only physically relevant, but also present many technical challenges in the pursuit to prove meaningful assertions about PDEs, this proposal bridges theoretical and applied mathematics. On the applied side, it is related to material microstructure (for example in alloys) and the emergence of complex macroscopic material behaviour from microscopic oscillations. On the theory side, oscillations and concentrations precisely distinguish between weak and strong compactness of sequences in Lebesgue and Sobolev spaces and “quantifying” this difference in a meaningful way is a pivotal goal of this project. Based on recently developed new tools, we aim to improve our understanding of these phenomena and to develop new applications to concrete PDE questions. Collaborations are planned with both applied and theoretical researchers in the field. Furthermore, as part of the grant, a research workshop on the topic will be organised.
4th February 2014
Martin Hairer & José Luis Rodrigo win ERC Consolidator grants
The European Research Council (ERC) has awarded two of its new ERC Consolidator Grants to Warwick mathematicians Martin Hairer and José Luis Rodrigo, the only awards in the UK for mathematics. A further two grants were awarded to Warwick in Chemistry. These prestigious new awards will enable already independent excellent researchers to consolidate their own research teams and to develop their most innovative ideas across the European Research Area.
President of the ERC, Professor Jean-Pierre Bourguignon commented: “I am very impressed by the quality of the selected projects. Judging by the ever increasing demand for ERC grants, especially from early- and mid-career researchers, it is clear that funding of this kind is much needed.”
European Commissioner for Research, Innovation and Science Máire Geoghegan-Quinn said: “These researchers are doing ground-breaking work that will advance our knowledge and make a difference to society. The ERC is supporting them at a key moment where funding is often hard to come by: when they need to move forward in their career and develop their own research and teams.”
Martin Hairer's project studies Behaviour near criticality. One of the main challenges of modern mathematical physics is to understand the behaviour of systems at or near criticality. In a number of cases, one can argue heuristically that this behaviour should be described by a nonlinear stochastic partial differential equation. Some examples of systems of interest are models of phase coexistence near the critical temperature, one-dimensional interface growth models, and models of absorption of a diffusing particle by random impurities. Unfortunately, the equations arising in all of these contexts are mathematically ill-posed to the extent that they defeat all current stochastic PDE techniques.
Recently, the theory of regularity structures has allowed us to give a rigorous mathematical interpretation to such equations and to build the mathematical objects conjectured to describe the above-mentioned systems near criticality. The aim of the proposal is to study the convergence of a variety of concrete microscopic models to these limiting objects. The project will yield unique insight in the large-scale behaviour of a number of physically relevant systems in regimes where both nonlinear effects and random fluctuations compete with equal strength.
José Luis Rodrigo's project concerns 3D Euler, Vortex Dynamics and PDE which deals with a collection of problems in analysis and partial differential equations arising from fluid mechanics. In particular, the main equation under consideration is the three dimensional Euler equation (for the evolution of an incompressible, inviscid fluid). Main objectives include the understanding of the evolution of isolated vortex lines for this equation, and the construction and understanding of the geometry and evolution of highly concentrated vortex tubes.
ERC Press release (PDF)