EPSRC Symposium Leslie Fox Prize
14th Leslie Fox Prize in Numerical Analysis
Warwick, Monday 29 June 2009
Abstracts
Stefano Giani (Nottingham University) A convergent adaptive method for elliptic eigenvalue problems
In the last decades, mesh adaptivity has been widely used to improve the accuracy of numerical solutions to many scientific problems. Recently the question of convergence of adaptive methods has received intensive interest and a number of convergence results for the adaptive solution of boundary value problems have appeared.
We proved the convergence of an adaptive linear finite element algorithm for computing eigenvalues and eigenvectors of scalar symmetric elliptic partial differential operators in bounded polygonal or polyhedral domains, subject to Dirichlet boundary data. Our refinement procedure is based on two locally defined quantities, firstly a standard a posteriori error estimator and secondly a measure of the variability (or “oscillation”) of the computed eigenfunction. Our algorithm performs local refinement on all elements on which the minimum of these two local quantities is sufficiently large. We prove that the adaptive method converges provided the initial mesh is sufficiently fine. The latter condition, while absent for adaptive methods for linear symmetric elliptic boundary value problems, commonly appears for nonlinear problems and can be thought of as a manifestation of the nonlinearity of the eigenvalue problem.
Daan Huybrechs (Katholieke Universiteit Leuven) On the Fourier extension of non-periodic functions
The topic of this talk is the use of classical Fourier series to approximate non-periodic functions. The Gibbs phenomenon can be entirely eliminated with a simple trick: a non-periodic function is extended to a function that is periodic on a larger domain. This approach has been proposed in several disciplines before. Yet, compared to other methods for defeating the Gibbs phenomenon, the analysis of this approach has been lacking. We present such analysis and in the process we arrive at several surprising conclusions. For example, non-periodic functions may be represented by a classical Fourier series, amenable to evaluation by FFT without modifications, with exponential accuracy. Our convergence theory is based on Chebyshev-like polynomials of the first and second kinds, and we find that the approach is in many ways dual to Chebsyshev expansions. We present and analyze stable numerical methods for constructing these series, in which the explicit construction of extensions is never required. An unexpected link to eigenfunctions of the Laplacian enables the generalization of our results to several interesting multivariate regions, including circles, triangles, tetrahedra and an infinite sequence of even higher-dimensional simplices, based on group theory and abstract algebra. Exponential accuracy is maintained in all these cases and, except for the case of the circle, the FFT may be used to evaluate the approximation.
Armin Lechleiter (CMAPX, Polytechnique) The factorization method is independent of transmission eigenvalues
As a rule of thumb, sampling methods for inverse scattering problems suffer from interior eigenvalues of the obstacle: if the wave number meets some resonance frequency of the scatterer, then these methods only work under suitable modification. Typically, such a modification requires a-priori knowledge on the scatterer, corrupting thereby the main advantage of sampling methods. It was common belief that transmission eigenvalues play a role corresponding to Dirichlet or Neumann eigenvalues in this respect. Surprisingly, this is not the case: the Factorization method is stable at transmission eigenvalues.
Colin B. Macdonald (Mathematics, UCLA) The Implicit Closest Point Method for the Numerical Solution of Partial Differential Equations on Surfaces (![]() pdf of file)
pdf of file)
The Closest Point Method is a recent numerical technique for solving partial differential equations (PDEs) on general surfaces. For example, it can be used to solve a pattern-formation PDE on the surface of a rabbit or evolve a curve on a bumpy surface as shown below.
 |
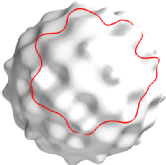 |
The Closest Point Method is simple to understand and implement. It combines standard finite difference schemes with an interpolation scheme in a narrow band enveloping the surface. However, the original formulation is designed to use explicit time stepping which may lead to a strict time-step restriction for some important PDEs.
In this presentation, I will describe an implicit Closest Point Method which allows large, stable time steps for high-order PDEs while retaining the principal benefits of the original method. Example computations (including the in-surface heat equation, reaction-diffusion on surfaces, Laplace-Beltrami eigenmodes, and fourth-order interface motion) on a variety of surfaces demonstrate the effectiveness of the method.
Brian D. Sutton (Randolph-Macon College) Computing the Complete CS Decomposition
In 1977, G. W. Stewart formulated the CS decomposition, utilizing earlier results of C. Davis and W. Kahan. We present an algorithm that computes the CS decomposition in its original and complete form; prior methods compute a reduced form, the 2-by-1 CSD. The complete CSD is similar to the eigenvalue and singular value decompositions but requires the simultaneous diagonalization of all four blocks of a 2-by-2 block unitary matrix. The decomposition can reveal the principal angles between a pair of linear subspaces (whose cosines and sines give the decomposition its name) and the canonical correlations between two sets of observed variables. It is related to the generalized singular value decomposition.
Liuqiang Zhong (Xiangtan University) Optimal multilevel and adaptive finite element methods for time-harmonic Maxwell equations
See also:
Mathematics Research Centre
Mathematical Interdisciplinary Research at Warwick (MIR@W)
Past Events
Past Symposia
Where possible, visitors should obtain an EDUROAM account from their own university to enable internet access whilst at Warwick.
You can register for any of the symposia or workshops online. To see which registrations are currently open and to submit a registration, please click hereLink opens in a new window.
Mathematics Research Centre
Zeeman Building
University of Warwick
Coventry CV4 7AL - UK
E-mail:
MRC@warwick.ac.uk

