Seminar organisers: Jan Grebík and Oleg Pikhurko
Warwick's combinatorics seminar in 2021-22 will be normally held 2-3pm UK time on Wednesdays in the hybrid format (in the room B3.02 and on ZOOM).
Term 3
The feasible region of induced graphs (Xizhi Liu), 14:00, B3.02 and ZOOM
Fix a graph F. A classical problem in extremal graph theory asks about how many induced copies of F can a graph with edge density ρ have? The only case in which we know the asymptotic solution is when F is a complete graph, and it was solved completely only recently by Reiher using the flag algebra machinery. We will consider the other cases and show some results when F is a complete bipartite graph or a complete graph minus one edge. Many interesting related open problems will also be introduced. Joint work with Dhruv Mubayi and Christian Reiher.
Trees in tournaments (Alistair Benford), 14:00, B3.02 and ZOOM
Given an n-vertex oriented tree T, what is the smallest size a tournament G must be, in order to guarantee G contains a copy of T? A strengthening of Sumner’s conjecture poses that it is enough for G to have (n+k-1) vertices, where k is the number of leaves of T. In this talk we will look at recent progress towards this conjecture. We shall also consider how this problem can be addressed by instead considering the maximum degree of the tree, rather than the number of leaves, and state some open problems in this maximum degree setting. This is joint work with Richard Montgomery.
The Alon-Jaeger-Tarsi conjecture via group ring identities (Péter Pál Pach), 14:00, B3.02 and ZOOM
The Alon-Jaeger-Tarsi conjecture states that for any finite field
F of size at least
4 and any nonsingular matrix
M over
F there exists a vector
x such that neither
x nor
Mx has a
0 component. In joint work with János Nagy we proved this conjecture when the size of the field is sufficiently large, namely, when
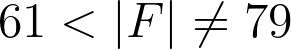
. In this talk we will discuss this result.
On the Ryser-Brualdi-Stein conjecture (Richard Montgomery), 14:00, B3.02 and ZOOM
The Ryser-Brualdi-Stein conjecture states that every Latin square of order
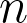
should have a partial transversal with

elements, and a full transversal if
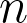
is odd. In 2020, Keevash, Pokrovskiy, Sudakov and Yepremyan improved the long-standing best known bounds on this conjecture by showing that a partial transversal with
)
elements always exists. I will discuss how to show, for large
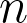
, that a partial transversal with

elements always exists.
Independent sets in random subgraphs of the hypercube (Gal Kronenberg), 14:00, B3.02 and ZOOM
Independent sets in bipartite regular graphs have been studied extensively in combinatorics, probability, computer science and more. The problem of counting independent sets is particularly interesting in the
d-dimensional hypercube
{0,1}d, motivated by the lattice gas hardcore model from statistical physics. Independent sets also turn out to be very interesting in the context of random graphs.
The number of independent sets in the hypercube
{0,1}d was estimated precisely by Korshunov and Sapozhenko in the 1980s and recently refined by Jenssen and Perkins.
In this talk we will discuss new results on the number of independent sets in a random subgraph of the hypercube. The results extend to the hardcore model and rely on an analysis of the antiferromagnetic Ising model on the hypercube.
This talk is based on joint work with Yinon Spinka.
Compact packings of the plane with discs (Miek Messerschmidt), 14:00, ZOOM only
After explaining what a compact packing of the plane by discs is, I will discuss the following question: "For which n-tuples of distinct positive real numbers is there a compact packing of the plane with discs, so that, firstly, only the mentioned n numbers are used as radii of discs in the packing, and secondly, every one of the mentioned n numbers occurs at least once as a radius of a disc in the packing?"
I will discuss some aspects of this question along with its history, which is surprisingly recent (e.g., the case n=2 was only solved in 2006).
Term 2
A tale of two balloons (Yinon Spinka), 16:00, ZOOM only
From each point of a Poisson point process start growing a balloon at rate 1. When two balloons touch, they pop and disappear. Will balloons reach the origin infinitely often or not? We answer this question for various underlying spaces. En route we find a new(ish) 0-1 law, and generalize bounds on independent sets that are factors of IID on trees.
Joint work with Omer Angel and Gourab Ray.
Perfect matchings and sandwich conjectures of random regular graphs (Jane Gao), 14:00, B3.02+ZOOM
In the first half of the talk I will survey results on the limiting distributions of small and large subgraphs of random regular graphs, and present a recent result on the limiting distribution of the number of perfect matchings. In the second half of the talk, I will talk about the Kim-Vu sandwich conjecture of random regular graphs, recent progress, and new results.
Big Ramsey degrees in binary free amalgamation classes (Andy Zucker), 16:00, ZOOM only
In structural Ramsey theory, one considers a "small" structure A, a "medium" structure B, a "large" structure C and a number r, then considers the following combinatorial question: given a coloring of the copies of A inside C in r colors, can we find a copy of B inside C all of whose copies of A receive just one color? For example, when C is the rational linear order and A and B are finite linear orders, then this follows from the finite version of the classical Ramsey theorem. More generally, when C is the Fraisse limit of a free amalgamation class in a finite relational language, then for any finite A and B in the given class, this can be done by a celebrated theorem of Nesetril and Rodl. Things get much more interesting when both B and C are infinite. For example, when B and C are the rational linear order and A is the two-element linear order, a pathological coloring due to Sierpinski shows that this cannot be done. However, if we weaken our demands and only ask for a copy of B inside C whose copies of A receive "few" colors, rather than just one color, we can succeed. For the two-element linear order, we can get down to two colors. For the three-element order, 16 colors. This number of colors is called the big Ramsey degree of a finite structure in a Fraisse class. Recently, building on groundbreaking work of Dobrinen, I proved a generalization of the Nesetril-Rodl theorem to binary free amalgamation classes defined by a finite forbidden set of irreducible structures (for instance, the class of triangle-free graphs), showing that every structure in every such class has a finite big Ramsey degree. My work only bounded the big Ramsey degrees, and left open what the exact values were. In recent joint work with Balko, Chodounsky, Dobrinen, Hubicka, Konecny, and Vena, we characterize the exact big Ramsey degree of every structure in every binary free amalgamation class defined by a finite forbidden set.
Recent Progress on Hadwiger's Conjecture (Michelle Delcourt), 14:00, B3.02+ZOOM
In 1943, Hadwiger conjectured that every graph with no Kt minor is (t-1)-colorable for every t ≥ 1. In a recent breakthrough, Norin, Song, and Postle proved that every graph with no Kt minor is O(t (log t)c)-colorable for every c > 0.25, Subsequently Postle showed that every graph with no Kt minor is O(t (log log t)6)-colorable. We improve upon this further showing that every graph with no Kt minor is O(t log log t)-colorable. Our main technical result yields this as well as a number of other interesting corollaries. A natural weakening of Hadwiger's Conjecture is the so-called Linear Hadwiger's Conjecture that every graph with no Kt minor is O(t)-colorable. We prove that Linear Hadwiger's Conjecture reduces to small graphs as well as that Linear Hadwiger's Conjecture holds for the class of Kr-free graphs (provided t is sufficiently large). This is joint work with Luke Postle.
Decidability and periodicity of translational tilings (Rachel Greenfeld), 16:00, ZOOM only
Translational tiling is a covering of a space using translated copies of some building blocks, called the “tiles”, without any positive measure overlaps. Which are the possible ways that a space can be tiled? In the talk, we will discuss the study of this question as well as its applications, and report on recent progress, joint with Terence Tao.
Packing list-colourings (Stijn Cambie), 14:00, B3.02+ZOOM
List colouring is an influential and classic topic in graph theory, which is related to e.g. frequency assignment, resource allocation and scheduling problems. Sometimes it is natural to consider multiple of these and the best one can aim for is a packing of disjoint solutions/ list colourings. We investigate this natural strengthening, the list packing problem.
This study was already suggested 25 years ago by Alon, Fellows and Hare. In this talk, we sketch the (conjectured) behaviour of this parameter and a related one under certain bounded degree conditions.
Stationary random graphs and groups (Mikolaj Fraczyk), 16:00, ZOOM only
A stationary random graph is a random rooted graphs (G,o) such that replacing the root o by its random neighbor results in the same probability distribution. The more well known unimodular random graphs are always stationary, but the unimodularity assumption is in fact much stronger. Invariant random subgroups and unimodular random graphs are now a household name in measured group theory, and they found several applications in geometry and topology. In my talk I want to advertise and describe some applications of the stationary random graphs and groups. I will explain how they can be used to find non-expander sub-graphs inside any given graph and how to prove that any higher rank locally symmetric space of infinite volume must have points of arbitrary large injectivity radius. The talk is based on a joint work with Wouter Van Limbeek and with Tsachik Gelander.
On measured expanders (Ján Špakula), 14:00, B3.02 and ZOOM
By a "measured graph" we simply mean a graph with weights assigned to its vertices. The classical isoperimetric (a.k.a. Cheeger) constant describing connectedness of a graph generalises to this setting, leading to a notion of a "measured expander": a sequence of finite graphs with a uniform positive lower bound on this isoperimetric
constant. The talk will walk through a bit of coarse geometry to a functional analytic question that led us to consider this notion. Our main result is a characterisation of measured expanders through a Poincare inequality, and thus that they do not coarsely embed into Lp-space. I will also present some examples. Based on joint work with K. Li and J. Zhang.
Labeled sample compression schemes for complexes of oriented
matroids (Victor Chepoi), 16:00, ZOOM only
The sample compression schemes were introduced by Littlestone and Warmuth in 1986 and have been vastly studied in the literature due to their importance in Machine Learning. Roughly speaking, the goal is to compress data as much as possible such that the original data can be reconstructed from the compressed data. The Vapnik-Chervonenkis dimension is central in Machine Learning and is important in Combinatorics and Discrete Geometry. Floyd and Warmuth in 1995 asked whether any set-family of VC-dimension d has a sample compression scheme of size O(d). This remains one of the oldest open problems in Machine Learning.
Recently we showed that the topes of a complex of oriented matroids (abbreviated COM) of VC-dimension d admit a proper labeled sample compression scheme of size d. This considerably extends results of Moran and Warmuth and the authors and is a step towards the sample compression conjecture. On the one hand, our approach exploits the rich combinatorial cell structure of COMs via oriented matroid theory. On the other hand viewing tope graphs of COMs as partial cubes creates a fruitful link to metric graph theory.
In the talk, we will expalain COMs and the labeled sample compression scheme for them.
Based on the paper:
V. Chepoi, K. Knauer, M. Philibert, Labeled sample compression schemes
for complexes of oriented matroids, arXiv:2110.15168, 2021.
Term 1
Factor of IID for the Ising model on the tree (Allan Sly), 14:00, B3.02+ZOOM
It's known that there are factors of IID for the free Ising model on the d-regular tree when it has a unique Gibbs measure and not when reconstruction holds (when it is not extremal). We construct a factor of IID for the free Ising model on the d-regular tree in (part of) its intermediate regime, where there is non-uniqueness but still extremality. The construction is via the limit of a system of stochastic differential equations.
Regularity Lemmas as Structured Decompositions (Henry Towsner), 14:00, B3.02+ZOOM
One way of viewing Szemerédi's regularity lemma is that it gives a way of decomposing a graph (approximately) into a structured part (the "unary" data) and a random part. Then hypergraph regularity, the generalization to k-uniform hypergraphs, can be viewed as a decomposition into multiple "tiers" of structure - a unary part as well as a binary part and so on, and then finally a random part.
We'll discuss how an analytic approach can make these decompositions exact instances of the conditional expectation in probability, and how these analytic proofs relate to combinatorial proofs with explicit bounds. Finally, we'll discuss regularity lemmas for other mathematical objects, focusing on the example of ordered graphs and hypergraphs, and show how the "tiers of structures" perspective makes it possible to see regularity lemmas for other mathematical objects as examples of the regularity lemma for hypergraphs.
(No prior knowledge of the regularity lemma and its variants is assumed.)
Cross-ratios and perfect matchings (Rob Silversmith), 14:00, B3.02+ZOOM
I’ll describe a simple process from algebraic geometry that takes in a collection of 4-element subsets S1,S2,…,Sn-3 of [n], and outputs a nonnegative integer called a cross-ratio degree. I’ll discuss several interpretations of cross-ratio degrees in algebra, algebraic geometry, and tropical geometry, and present a combinatorial algorithm for computing them, due to C. Goldner. I’ll then present a perhaps-surprising upper bound for cross-ratio degrees in terms of matchings.
Progress on the Kohayakawa-Kreuter conjecture (Joseph Hyde), 14:00, B3.02+ZOOM
Let H
1, ..., H
r be graphs. We write G(n,p) → (H
1, ..., H
r) to denote the property that whenever we colour the edges of G(n,p) with colours from the set [r] := {1, ..., r} there exists some 1 ≤ i ≤ r and a copy of H
i in G(n,p) monochromatic in colour i.
There has been much interest in determining the asymptotic threshold function for this property. Rödl and Ruciński (1995) determined the threshold function for the general symmetric case; that is, when H1 = ... = Hr. A conjecture of Kohayakawa and Kreuter (1997), if true, would effectively resolve the asymmetric problem. Recently, the 1-statement of this conjecture was confirmed by Mousset, Nenadov and Samotij (2021+). The 0-statement however has only been proved for pairs of cycles, pairs of cliques and pairs of a clique and a cycle.
In this talk we introduce a reduction of the 0-statement of Kohayakawa and Kreuter's conjecture to a certain deterministic, natural subproblem. To demonstrate the potential of this approach, we show this subproblem can be resolved for almost all pairs of regular graphs (satisfying properties one can assume when proving the 0-statement).
Directed analogues of expander graphs and random compact subsets ot Rn (Lukasz Grabowski), 14:00, B3.02+ZOOM
I will talk about two separate projects. The first one is a joint work with Endre Csoka (published in "Combinatorics, Probability and Computing"), where we construct "extender" graphs - sparse directed graphs with the property that it is impossible to remove a small amount of edges and obtain a graph which does not have long directed paths (long is
|V|
δ, where δ>0 is an absolute constant). Extenders are a directed analogue of expander graphs, since the latter ones are characterised by the property that it is impossible to remove a small amount of edges and obtain graphs which have small connected components. I'll discuss some conjectures in circuit complexity which motivated us to introduce extenders.
The second project is a joint work with Tomasz Ciesla (preprint available on arxiv). We construct compacts subsets of
R2 which are not "domains of expansion", which answers a question about spectral properties of group actions, raised by Adrian Ioana.
Apart from the general theme of "expansion", both projects are related by the method which is used to construct suitable examples - in both cases the construction is probabilistic, and the required properties follow from entropy estimates.
Uncommon systems of equations (Natasha Morrison), 16:00, ZOOM only
A system of linear equations
L over
Fq is
common if the number of monochromatic solutions to
L in any two-colouring of
(Fq)
n is asymptotically at least the expected number of monochromatic solutions in a random two-colouring of (
Fq)
n. Motivated by existing results for specific systems (such as Schur triples and arithmetic progressions), as well as extensive research on common and Sidorenko graphs, the systematic study of common systems of linear equations was recently initiated by Saad and Wolf. Building on earlier work of of Cameron, Cilleruelo and Serra, as well as Saad and Wolf, common linear equations have been fully characterised by Fox, Pham and Zhao.
In this talk I will discuss some recent progress towards a characterisation of common systems of two or more equations. In particular we prove that any system containing an arithmetic progression of length four is uncommon, confirming a conjecture of Saad and Wolf. This follows from a more general result which allows us to deduce the uncommonness of a general system from certain properties of one- or two-equation subsystems.
Asymptotic dimension of graph classes (Carla Groenland), 14:00, B3.02+ZOOM
The notion of asymptotic dimension of graph classes is borrowed from an invariant of metric spaces introduced by Gromov in the context of geometric group theory. In the talk, I will try to give some intuition for the definition and our proof techniques. Our main result is that each minor-closed family of graphs has asymptotic dimension at most 2. I will also mention some corollaries to clustered colouring and CS notions such as weak sparse partition schemes and weak diameter network decompositions. A special case of our main result also implies that complete Riemannian surfaces have asymptotic dimension (even Assouad-Nagata dimension) at most 2 (which was previously unknown).
This is based on joint work with M. Bonamy, N. Bousquet, L. Esperet, C.-H. Liu, F. Pirot and A. Scott.
Some modern open problems on polytopes with symmetries and regularities (Martin Winter), 14:00, B3.02+ZOOM, Recording passcode: f5FB!YDJ
Polytope theory has itself established as a modern field of mathematics with deep connections to geometry, combinatorics, and algebra. Convex polytopes with many symmetries and regularities however have thereby played only a secondary role and are often considered as a fascinating, yet esoteric subject of the past. In this talk I want to rectify this by presenting up to three modern open problems that connect the study of such polytopes to representation theory, hyperplane arrangements and Weyl groupoids, as well as spectral graph theory. More specifically, the three topics are the possible symmetries of orbit polytopes, inscribed and simple zonotopes, and the reconstruction of polytopes from graphs via spectral graph theory.
Equivariant Cayley Complex Embeddings (George Kontogeorgiou), 14:00, B3.02+ZOOM
In recent years, a lot of progress has been made in high-dimensional combinatorics, i.e. extending concepts from graph theory to higher dimensional CW-complexes. Two such concepts of particular interest are (i) group actions and (ii) embeddings. In this talk we will prove that every finite group which admits a faithful topological action over S3 has a generalised Cayley complex which embeds equivariantly in S3. In the process, we will see some recent theorems and lemmas concerning 2-complex embeddings and group actions over 2-complexes, and we will derive a new combinatorial characterization of finite groups acting faithfully and topologically over S3.
