Tropical Geometry

Diane Maclagan has been awarded an ESPRC Open Plus Fellowship to investigate the fascinating foundations of tropical geometry.

Tropical geometry is geometry over the tropical semiring (see sidebar). A major focus of the subject is to study varieties from algebraic geometry (the solutions to systems of multivariate polynomial equations) by their "combinatorial shadow" (tropical varieties). Tropical polynomials are piecewise linear functions, and their solutions are union of polyhedra. The picture below shows the tropicalization of an elliptic curve. This "shadow" reflects some of the geometry of the curve: the cycle reflects that elliptic curves have genus one (are topologically tori), and the length of the cycle encodes some information about the $j$-invariant of the curve.

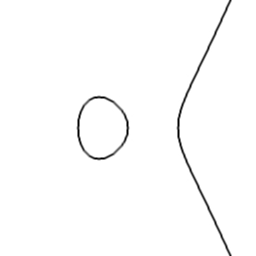
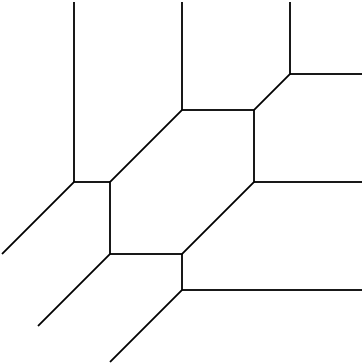
[ell1.jpg] [tropicalCubic.pdf] [can get better resolution of both]

As well as applications inside algebraic geometry, to mirror symmetry, enumerative geometry, log geometry, and real algebraic geometry, tropical methods also appear across mathematics and its applications. A prominent recent example is June Huh's applications of combinatorial Hodge theory to combinatorics, in which tropicalizations of matroids play a crucial role. Tropical ideals also appear in economics, machine learning, optimization, and phylogenetics (and famously once helped design the Dutch train schedule!).

Diane Maclagan was awarded an ESPRC Open Plus Fellowship to work on the foundations of tropical geometry, and in particular work on tropical schemes. This involves developing a theory of commutative algebra in the tropical setting, and associated geometric ideas. Matroids and their generalisations play a starring role in this story.