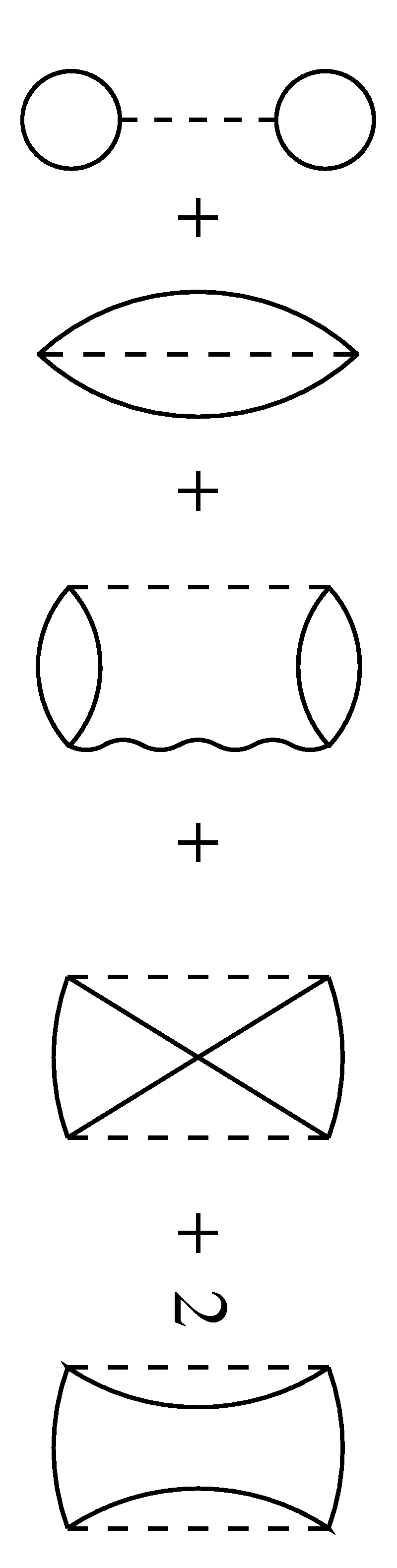Equation of State of Dense Plasmas

 

Analytical Calculations

For densities that usually correspond to some kind of vacuum and for densities orders of magnitude higher than common on earth (only to be found in stars, giant planets, dwarfs and in some high energy experiments) the equation of state (EOS) and other thermodynamic properties can be calculated with the help of quantum statistical Green's functions. One usually derives a very general perturbation expansion in terms of the interaction strength. Advantage: almost no computational effort by todays standards, description from first principles and exact in limiting cases. Disadvantage: restricted to certain physical parameter regions and very simple materials due to complexity.

Numerical Calculations

Computer simulations like MC, MD, PIMC, QMC, DFT and DFT-MD have increased the hopes of physicists to describe (complex) matter from first principles. By today it is possible to compute the thermodynamic conditions inside planets entirely from ab initio simulations and describe interiors of giant gas planets and extrasolar planets. Following experimental observations and even predicting new properties of matter under high pressure, DFT and other quantum simulation techniques have proven to be a reliable tool.

Nonequilibrium Properties 

The creation and time evolution into the equilibrium state of matter under extreme conditions is governed by nonequilibrium quantities such as stopping power, energy transfer rates, collisional cross sections, collision frequencies, and self energies. They are closely related to pure equilibrium quantities but require special attention in situations far from equilibrium. Quantum kinetic theory on the basis of Green's functions is required to model the complex physical processes in nonequilibrium situations. Focus point at the moment is the energy transfer rate which describes how an initial two temperature plasma will, by showing complex ionization, recombination, and correlation phenomena, relax into equilibrium.

Publications

• D.O. Gericke, J. Vorberger, K. Wünsch, G. Gregori, Phys. Rev. E 81, 065401 (2010)
  
• J. Vorberger, D.O. Gericke, Th. Bornath, M. Schlanges, Phys. Rev. E 81, 046404 (2010)
  
• A.L. Kritcher, P. Neumayer, C.R.D. Brown, P. Davis, T. Döppner, R.W. Falcone, D.O. Gericke, G. Gregori, B. Holst, O.L. Landen, H.J. Lee, E.C. Morse, A. Pelka, R. Redmer, M. Roth, J. Vorberger, K. Wünsch, S.H. Glenzer, Phys. Rev. Lett. 103, 245004 (2009)
  
• J. Vorberger, D.O. Gericke, Physics of Plasmas 16, 082702 (2009)
  
• B. Barbrel, M. Koenig, A. Benuzzi-Mounaix, E. Brambrink, C.R. Brown, D.O. Gericke, B. Nagler, M. Rabec le Gloahec, D. Riley, C. Spindloe, S.M. Vinko, J. Vorberger, J. Wark, K. Wünsch, and G. Gregori, Phys. Rev. Lett. 102, 165004 (2009)
  
• K. Wünsch, J. Vorberger, D.O. Gericke, Phys. Rev. E 79 010201(R) (2009)
  
• J. Vorberger, J. Phys. A 42, 214062 (2009)
  
• B. Militzer, W.B. Hubbard, J. Vorberger, I. Tamblyn, and S.A. Bonev, ApJ 688, L45 (2008)
  
• A. Grinenko, D.O. Gericke, S.H. Glenzer, and J. Vorberger, Phys. Rev. Lett. 101, 194801 (2008)
• E. Garcia Saiz, G. Gregori, D.O. Gericke, J. Vorberger et al., Nature Phys. 4, 940 (2008)
  
• J. Vorberger, I. Tamblyn, S.A. Bonev, B.Militzer,Contrib. Plasma Phys. 47, 267 (2007), Properties of Dense Fluid Hydrogen and Helium in Giant Gas Planets
• W.-D. Kraeft, J.Vorberger, D.O.Gericke, M. Schlanges,Contrib. Plasma Phys. 47, 253 (2007), Thermodynamic Functions for Plasmas beyond Montroll Ward
• J. Vorberger, I. Tamblyn, S.A. Bonev, B. Militzer, Phys. Rev. B 75, 024206 (2007), Hydrogen-Helium Mixtures in the Interiors of Giant Planets
• J. Vorberger, M. Schlanges, D.O. Gericke, W.-D. Kraeft,J. Phys. A: Math. Gen. 39, 4707 (2006), Equation of State of High Density Plasmas
• M. Schlanges, V. Bezkrovniy, J. Vorberger, D. Kremp, W.-D. Kraeft,Contrib. Plasma Phys. 45, 405 (2005), Thermodynamic Properties of Dense Hydrogen
• J. Vorberger, D.O. Gericke, in GSI Annual Report 2004, High Energy Density Physics with Intense Laser and Ion Beams (GSI,Darmstadt, 2005, p. 47), Collective Modes and Energy Transfer Rates in Two-Temperature-Plasmas
• J. Vorberger, M. Schlanges, W.-D. Kraeft, Phys. Rev. E 69, 046407 (2004), Equation of State for Weakly Coupled Quantum Plasmas
• J. Vorberger, M. Schlanges, W.-D. Kraeft in {\it Equation of State and Phase Transition Issues in Models of Ordinary Astrophysical Matter}, V. Celebonovic, W. Däppen, D. Gough (Eds.), AIP conference proceedings 731, Melville (2004), Quantum Statistical Approach to Dense, Weakly Coupled Plasmas
• J. Vorberger, M. Schlanges, W.-D. Kraeft in High Energy Density in Matter with Intense Laser and Ion Beams, GSI Annual Report (2004), Equation of State for Weakly Coupled Quantum Plasmas
• J. Vorberger, M. Schlanges, W.-D. Kraeft in ICPIG XXVI International Conference on Phenomena in Ionized Gases, J. Meichsner, D. Loffhagen, H.-E. Wagner (Eds.), Greifswald (2003), Thermodynamic Properties of Plasmas at High Densities
• M. Schlanges, J. Vorberger, H.E. DeWitt, W.-D. Kraeft,J. Phys. A: Math. Gen. 36 (22), 5949 (2003), Equation of State and Correlation Energy of Dense Plasmas
• J. Vorberger, M. Schlanges, W.-D. Kraeft, H.E. DeWitt in Progress in Nonequilibrium Green's Functions II, M. Bonitz, D. Semkat (Eds.), World Scientific, New Jersey (2003), Thermodynamic Functions of Dense Quantum Plasmas
• W.-D. Kraeft, M. Schlanges, J. Vorberger, H.E. DeWitt,Phys. Rev. E 66, 046405 (2002), Kinetic and Correlation Energies and Distribution Functions of Dense Plasmas
• J. Vorberger, M. Schlanges, W.-D. Kraeft in High Energy Density in Matter Produced by Heavy Ion Beams, GSI Annual Report (2001), Equation of State for Dense Quantum Plasmas
• J. Vorberger, M. Schlanges, J. Riemann, W.-D. Kraeft in High Energy Density in Matter Produced by Heavy Ion Beams, GSI Annual Report (2000), Thermodynamics of Degenerate Plasmas, Analytics vs. Numerics

CV 

curriculum vitae