Relaxation in NMR describes the non-radiative transfer of energy that allows nuclear spins to undergo a transition from an excited state to a ground state. This process can be attributed to two relaxation mechanisms; spin-lattice relaxation and spin-spin relaxation. Nuclei with a non-zero spin possess an inherent nuclear magnetic moment. Spin-spin relaxation refers to the interaction of the nuclear magnetic moment with a magnetic field oscillating around the larmor frequency. Spin-lattice refers to the restoration of thermal equilibrium characterised by the Boltzman distribution via the dissipation of energy to the lattice. The rates of relaxation are dictated by the reciprocals of the time constants T_2 and T_1 respectively.

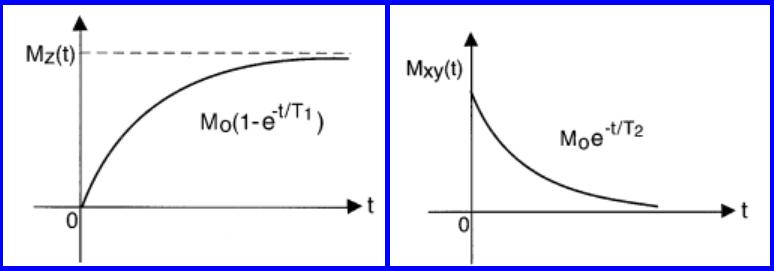
These parameters are important experimentally as T1 provides insight into the repetition time of a NMR experiment, whereas T2 is directly related to the lifetime of the excited state. Relaxation is dependent on the local environments the nuclei inhabit, thus relaxation can provide information on the chemistry of a sample.

Measurement of T1 and T2

Inversion-recovery

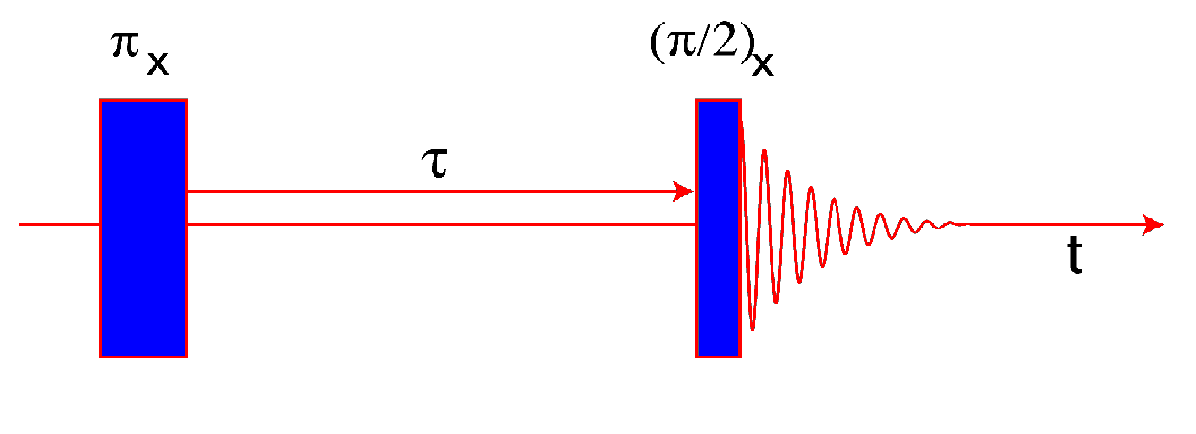
Basic pulse sequence:

• (π) r.f. pulse along the x-axis

This causes a nuclear spin state population inversion, so the net magnetisation is reversed.

• Interval of nuclear spin evolution (τ)

The relaxation of the nuclear spins means that the magnetisation grows towards the value it attained at thermal equilibrium

• (π/2) r.f. pulse along the x-axis

This rotates the recovered magnetisation after (τ) into the transverse plane; it creates coherences.

• The signal is acquired over the interval (t)

The coherence includes the observable (-1)-quantum coherence that induces an NMR signal

The experiment is repeated with the value of (τ) arrayed. To reduce errors due to poor signal to noise for each value of (τ) the pulse sequence is repeated and data is acquired numerous times so that the signals can be added together. These repeated experiments are separated by a time interval that should be of the order 5*T1 . This highlights a disadvantage of the inversion-recovery experiment; it requires at least a rough idea of T_1 beforehand.
The spectral peak amplitudes are plotted against τ. As τ approaches the spin-lattice relaxation value the final (π/2) pulse should send more nuclear spins into the (-1)-quantum coherence and more signal should be generated.

This can be fitted with a curve - a(τ) α 1/2(1-2e^(-τ/T1 ))

Then T1 is extracted by taking logs to create a linear equation where the gradient (m) is equal to 1/T1

y=mx+c

log((a(τ) )=τ/T1 +c

Spin-echo

A spin-echo pulse sequence is used to eliminate dephasing in nuclear spins due to inhomogeneity in the externally applied magnetic field.
The signal in an NMR experiment is the detection of a current in a coil that is induced by the precession of the net magnetisation around the direction of the external magnetic field, where the net magnetisation is the superposition of all the nuclear magnetic moments in the sample. The larmor frequency of a spin (and therefore the nuclear magnetic moment) is sensitive to the local environment. A difference in the magnetic field at the nucleus causes a difference in the larmor frequency. Larger differences cause a more rapid level of dephasing (and thus a more rapid loss of signal). Dephasing is an unavoidable mechanism for relaxation due to the spin-spin interactions, which is described by T2. Depahsing become more rapid due to the presence of inhomogeneity in the external magnetic field, which is accommodated for by the use of T2*.
The inhomogeneity is the reason that one cannot simply use the NMR spectral peaks to determine T2 (via the relation width-at-half-height= 1/(πT2 )) as it causes peak broadening.

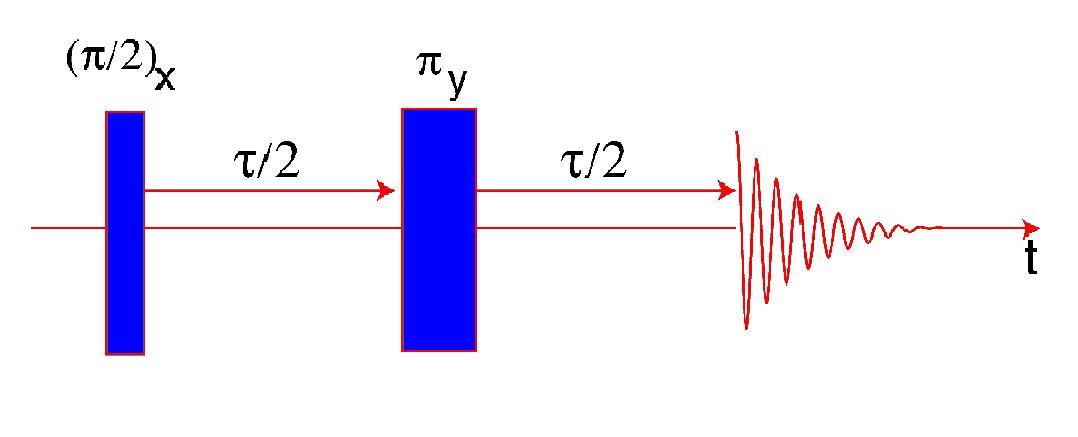
Basic pulse sequence:

• (π/2)_xr.f. pulse along the x-axis

This produces transverse magnetisation

• Interval of nuclear spin evolution (τ/2)

As the transverse magnetisation precesses, it shrinks due to dephasing cause by spin-spin interactions and inhomogeneity in the external magnetic field

• (π) r.f. pulse along the y-axis

This pulse maintains the phase differences that will have developed after the spins evolution after the initial pulse.

• Interval of nuclear spin evolution (τ/2)

The inversion means that spins in a stronger magnetic environment and therefore precessing at a higher larmor frequency rephrase so that the signal grows strong up until the end of the interval (τ/2)

• The signal is acquired over the interval (t)

Again the experiment is repeated for different values of (τ).

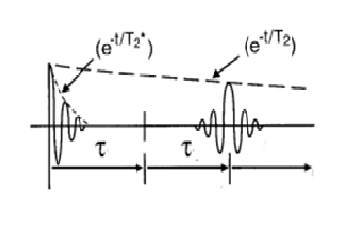The spectral peak amplitudes are plotted against τ.

a(τ) α 1/2 e^(-τ/T2 )

This can be solved for T2 by taking logs and plotting the linear function that results. The gradient of the line will be the reciprocal of T2.

log(a(τ) )=-τ/T2 +c

---

These diagrams have been adapted from Malcolm Levitt's 'Spin Dynamics: basics of nuclear magnetic resonance'; 2nd ed. ed. (2000)

&

Ray H. Hashemi ,William G. Bradley , Christopher J. Lisanti text book 'MRI The Basics', 3rd ed, (2010);