Here is a link to the wiki page concerning the topic I mentionned towards the end of todays reading group:
https://en.wikipedia.org/wiki/Stein%27s_example
It is worth knowing about the Stein paradox since it is the precursor of the idea of shrinkage and penalized estimation in statistics.
when I scrolled through this, it rang a bell. I know of course Stein's lemma which is simply Gaussian partial integration, and when I heard of Stein's lemma long time ago, people must have mentioned Stein's paradox, too.
however, I noticed that the shrinkage estimator used for showing the paradox does NOT require any knowledge of the true parameter, while the shrunken estimators I discussed, but also those shalin referenced in his second forum post, depend on the true parameter which would be the true distribution function in the "worst" case. and, different to the paradox, these shrunken estimators work in all dimensions. and the linear shrinkage ones would shrink both mean square error and variance---checked for the unbiased case. but bias would go up after performing shrinkage, though I could calculate the bound 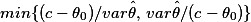again in the unbiased case (the lower bound would be the reciprocal of the sum of the two terms under the min).
so, doing shrinkage repeatedly may give a biased estimator, in the end, but there is hope that the bias is on the same scale as the shrunken variance in the penultimate step if 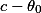is good enough, AND THIS WOULD JUSTIFY SHRINKING THE VARIANCE WITHOUT THINKING ABOUT CREATING BIAS. verifying the latter seems easy for linear shrinkage but might be involved for other shrinkage methods---care has to be taken. eventually, if the sample size is big enough, then the empirical distribution should be close enough to the true one, and hence it should be fine to start the shrinkage iteration with the empirical distribution which means bootstrapping.
