Modelling methodology developed by Sbider

Epidemic modelling
Mathematical modelling of infectious diseases is used to study the mechanisms by which diseases spread, to predict the future course of an outbreak and to determine which control strategies are most effective and cost-effective.
Modelling infectious diseases
Sbider experts are are the forefront of the development and application of cutting-edge epidemiological models.Cell surface analysis and mathematical modelling
Macropinocytosis is a broadly conserved endocytic process discovered nearly 100 years ago, yet still poorly understood. Macropinocytic cells extend large cups or flaps from their plasma membrane to engulf droplets of medium and trap them in micron-sized vesicles. Here they are digested and the products absorbed. Experts in Sbider have used mathematical modelling to understand how cups are shaped and closed.

Macropinocytosis model
A) Dictyostelium cell performing macropinocytosis by forming cups from PIP3-rich domains on the membrane by means of actin polymerization at the edge of the domain.
B) segmented surface of the cell with local maximum fluorescence intensity assigned to each vertex on the surface.
C) structures can also be generated with a surface model containing a PIP3 domain of fixed area with forces applied at its boundary. Purple: PIP3, Green: Nucleator of Actin polymerisation.

Modelling plant symbiosis
To understand plant responses to stress and during symbiosis we are developing a spatiotemporal framework including many data types or modalities, gathered using high-throughput techniques.
Multi-modal modelling
Integrating information from both the molecular, physiological and phenotypic levels is essential if we are to characterise biological processes.
Multi-physics and multi-scale modelling
Multi-physics and multi-scale modelling frameworks have been deployed successfully by Sbider members to tackle problems at disciplinary interfaces. One such example is the development and usage of computational fluid mechanics tools alongside rheological or advective-diffusive features for chemical species in order to model processes as part of applications such as bioreactor or needle design.
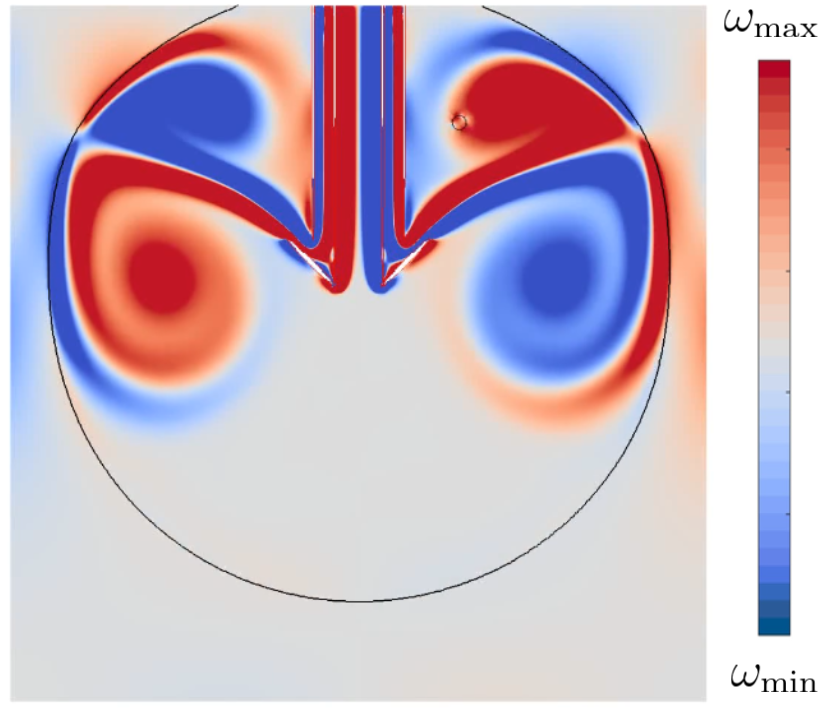
Needle design for IVF
Models were used to study the complex flow of liquid through needles used for IVF, and help improve the design. The figure shows the vorticity field ω monitored inside a follicular environment using a computational fluid dynamics model to describe fluid movement and enable the design of new flow-informed needle features.

Epidemiology and evolution
Phylodynamic modelling can bridge the gap between the epidemiology and the evolution of infectious pathogens.
Phylodynamic modelling
Modelling responsive hydrogels
Hydrogels are soft, porous, elastic materials comprising hydrophilic polymer chains surrounded by adsorbed water molecules and are found naturally in biological tissues (gelatin and cellulose gels), but also find increasing use in implantable biomedical devices and wound healing. Bringing together insights from fluid dynamics, nonlinear elasticity and thermodynamics, Sbider experts have developed a linear-elastic-nonlinear-swelling (LENS) theory for modelling hydrogels and their response to changes in temperature and chemical concentration.

LENS theory
The model is analytically tractable and formulated as coupled PDEs, allowing us to model the flow of water throughout the porous gel and the transient elastic response as well as finding the steady states. This approach lends itself to the development of microfluidic displacement pumps, which respond to pulses of heat to drive flow, or in the modelling of tissues, which share many structural similarities with super-absorbent gels.
