Mathematical problems for self assessment

Sample Problems

FIRST ORDER ORDINARY DIFFERENTIAL EQUATIONS

 

1. For the following differential equations, state their order and whether they are linear or nonlinear equations:

(i)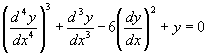

(ii)

(iii)

(iv)

[Ans. (i) order 4, nonlinear, (ii) order 3, linear, (iii) order 1, nonlinear, (iv) order 1, linear].

 

2. Verify that the function solves the differential equation

 

3. Determine the differential equations satisfied by the following functions:

(i)

(ii)

[Ans. (i) (ii) ].

 

4. Find the solutions of the following differential equations by direct integration:

(i)

(ii) ,

(iii)

[Ans. (i) , (ii) , (iii) ].

 

5. Find, by separation of variables, the particular solutions of the differential equations:

(i) , y(-2) =4,

(ii) , .

[Ans. (i) , (ii) ].

 

6. Find, by separation of variables, the general solutions of the differential equations:

(i) ,

(ii) .

[Ans. (i) , (ii) ].

 

7. By finding an appropriate integrating factor determine the general solutions of the following linear ordinary differential equations:

(i) ,

(ii) .

[Ans. (i) , (ii) ].

 

8. By finding an appropriate integrating factor determine the particular solution of the linear ordinary differential equation

, .

[Ans. ].

 

9. In an circuit with applied voltage ,the instantaneous current i(t) in the circuit satisfies the first order ordinary differential equation

with initial condition . Find the particular solution of this linear ODE.

[Ans. ].

 

10. (The Bernoulli Equation) Consider the nonlinear ordinary differential equation given by

, for

and appropriate functions and . This equation is called the Bernoulli equation and it has particular applications in fluid mechanics and civil engineering problems. Show that by making the substitution , this equation can be expressed in the form

,

which is a linear equation that can be solved in the standard way using the integrating factor technique.

Hence find the general solution of the Bernoulli equation

.

[Ans. ].