Usually, the main calculation when designing a DRWH system will be to size the water tank correctly to give adequate storage capacity. The storage requirement will be determined by a number of interrelated factors. They include:

• local rainfall data and weather patterns
• roof (or other) collection area
• runoff coefficient (this varies between 0.5 and 0.9 depending on roof material and slope)
• user numbers and consumption rates

The style of rainwater harvesting will also play a part in determining the system components and their size.

There are a number of different methods for sizing system components. These methods vary in complexity and sophistication. Some are readily carried out by relatively inexperienced first-time practitioners; others require computer software and trained engineers who understand how to use this software. The choice of method used to design system components will depend largely on the following factors:

• the size and sophistication of the system and its components
• the availability of the tools required for using a particular method (e.g. computers)
• the skill and education levels of the practitioner / designer

Below we will outline 3 different methods for sizing RWH system components.

Method 1 demand side approach

A very simple method is to calculate the largest storage requirement based on the consumption rates and occupancy of the building.

As a simple example we can use the following typical data:

• Consumption per capita per day, C – 20 litres
• Number of people per household, n – 6
• Longest average dry period – 25 days

Annual consumption = C x n x 365 = 43,800 litres

Storage requirement, T = (43,800 x 25) / 365 = 3,000 litres

This simple method assumes sufficient rainfall and catchment area which is adequate, and is therefore only applicable in areas where this is the situation. It is a method for acquiring rough estimates of tank size.

Method 2 – supply side approach

In low rainfall areas or areas where the rainfall is of uneven distribution, more care has to be taken to size the storage properly. During some months of the year there may be an excess of water, while at other times there will be a deficit (see figure 1). If there is sufficient water throughout the year to meet the demand, then sufficient storage will be required to bridge the periods of scarcity. As storage is expensive, this should be done carefully to avoid unnecessary expense.

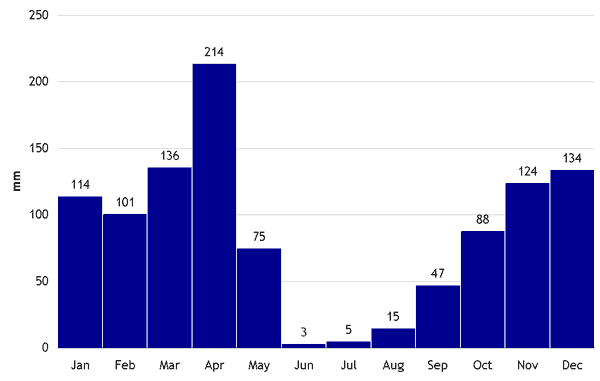
Figure 1: Average rainfall for Biharamulo District

The example given here is a simple spreadsheet calculation for a site in North Western Tanzania. The rainfall statistics were gleaned from a nurse at the local hospital who had been keeping records for the previous 12 years. Average figures for the rainfall data were used to simplify the calculation, and no reliability calculation is done. This is a typical field approach to RWH storage sizing.

Example
Site: Medical dispensary, Ruganzu, Biharamulo District, Kagera, Tanzania (1997)

Demand:

• Number of staff: 7
• Staff consumption: 45 litres per day x 7 = 315 litres per day
• Patients: 40 
• Patient consumption : 10 litres per day x 40 = 400 litres per day

Total demand: 715 litres per day or 21.75 cubic metres per mean month

Supply:

• Roof area: 190m²
• Runoff coefficient (for new corrugated GI roof): 0.9
• Average annual rainfall: 1056mm per year
• Annual available water (assuming all is collected) = 190 x 1.056 x 0.9 = 180.58m³

Daily available water = 180.58 / 365 = 0.4947 m³ / day or 494.7 litres per day or 15.05 cubic metres per mean month

So, if we want to supply water all the year to meet the needs of the dispensary, the demand cannot exceed 494.7 litres per day. The expected demand cannot be met by the available harvested water. Careful water management will therefore be required.

Figure 2: comparison of the harvestable water and the demand for each month

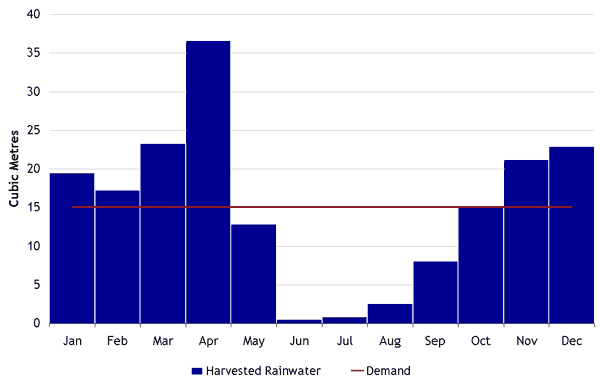
Figure 2 shows the comparison of water harvested and the amount that can be supplied to the dispensary using all the water which is harvested. It can be noted that there is a single rainy season. The first month that the rainfall on the roof meets the demand is October. If we therefore assume that the tank is empty at the end of September we can form a graph of cumulative harvested water and cumulative demand and from this we can calculate the maximum storage requirement for the dispensary.

Figure 3: showing the predicted cumulative inflow and outflow from the tank. The maximum storage requirement occurs in April

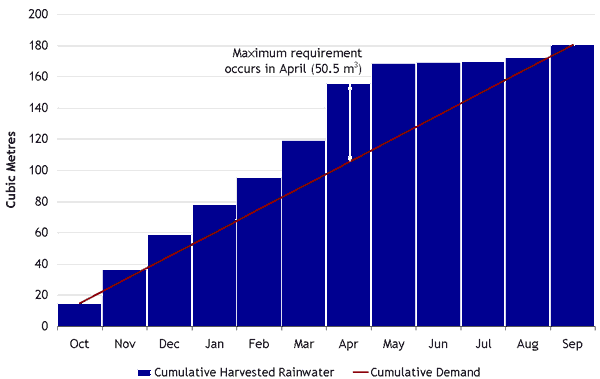
Table 1 - shows the spreadsheet calculation for sizing the storage tank. It takes into consideration the accumulated inflow and outflow from the tank and the capacity of the tank is calculated as the greatest excess of water over and above consumption. This occurs in April with a storage requirement of 50.45 cubic metres. All this water will have to be stored to cover the shortfall during the dry period.

Table 1

Month	Rainfall (mm)	Rainfall harvested (cubic metres)	Cumulative rainfall harvested (cubic metres)	Demand (based on total utilisation)	Cumulative demand (cubic metres)	Difference between column 4 and 6
Oct	88	15.05	15.05	15.05	15.05	0.00
Nov	124	21.20	36.25	15.05	30.10	6.16
Dec	134	22.91	59.17	15.05	45.14	14.02
Jan	114	19.49	78.66	15.05	60.19	18.47
Feb	101	17.27	95.93	15.05	75.24	20.69
Mar	136	23.26	119.19	15.05	90.29	28.90
Apr	214	36.59	155.78	15.05	105.34	50.45
May	75	12.83	168.61	15.05	120.38	48.22
Jun	3	0.51	169.12	15.05	135.43	33.69
Jul	5	0.86	169.97	15.05	150.48	19.49
Aug	15	2.57	172.54	15.05	165.53	7.01
Sep	47	8.04	180.58	15.05	180.58	0.00
Totals		180.58		180.58

Method 3 – computer model

There are several computer-based programmes for calculating tank size quite accurately. One such programme, known as SimTanka, has been written by an Indian organisation and is available free of charge on the World Wide Web. The Ajit Foundation is a registered non-profit voluntary organisation with its main office in Jaipur, India and its community resource centre in Bikaner, India.

SimTanka is a software programme for simulating performance of rainwater harvesting systems with covered water storage tank. Such systems are called Tanka in western parts of the state of Rajasthan in India.

The idea of a computer simulation is to predict the performance of a rainwater harvesting system based on the mathematical model of the actual system. In particular SimTanka simulates the fluctuating rainfall on which the rainwater harvesting system is dependent.

Rainwater harvesting systems are often designed using some statistical indicator of the rainfall for a given place, like the average rainfall. When the rainfall is meagre and shows large fluctuations then a design based on any single statistical indicator can be misleading. SimTanka takes into account the fluctuations in the rainfall, giving each fluctuation its right importance for determining the size of the rainwater harvesting system. The result of the simulation allows you to design a rainwater harvesting system that will meet demands reliably, that is, it allows you to find the minimum catchment area and the smallest possible storage tank that will meet your demand with probability of up to 95% in spite of the fluctuations in the rainfall. Or you can use SimTanka to find out what fraction of your total demand can be met reliably.

SimTanka requires at least 15 years of monthly rainfall records for the place at which the rainwater harvesting system is located. If you do not have the rainfall record for the place then the rainfall record from the nearest place which has the same PATTERN of rainfall can be used.

The included utility, RainRecorder, is used for entering the rainfall data. Daily consumption per person is also entered and then the software will calculate optimum storage size or catchment size depending on the requirements of the user. SimTanka also calculates the reliability of the system based on the rainfall data of the previous 15 years.

SimTanka is free and is and was developed by the Ajit Foundation in the spirit that it might be useful for meeting the water needs of small communities in a sustainable and reliable manner. But no guaranties of any kind are implied.

For more information or to download the software see their website at http://homepage.mac.com/vsvyas/science.html

(Source: the information given here is taken from this website).

Further comments

These methods outlined above can be further refined where necessary to use daily rainfall data. This is particularly important in areas where rainfall is more evenly distributed and more sensitive calculations are necessary.

Rainfall data can be obtained from a variety of sources. The first point of call should be the national meteorological organisation for the country in question. In some developing countries, however, statistics are limited due to lack of resources and other sources are often worth seeking. Local Water Departments or organisations, local hospitals or schools are all possible sources of information.

In reality the cost of the tank materials will often govern the choice of tank size. In other cases, such as large RWH programmes, standard sizes of tank are used regardless of consumption patterns, roof size or number of individual users.

Tank efficiency and the case for diminishing returns

On days when rainfall is heavy, the flow into a tank is higher than the outflow drawn by water users. A small tank will soon become full and then start to overflow. An inefficient system is one where, taken over say a year, that overflow constitutes a significant fraction of the water flowing into the tank. Insufficient storage volume is however not the only cause of inefficiency: poor guttering will fail to catch water during intense rain, leaking tanks will lose water, and an ‘oversize’ roof will intercept more rainfall than is needed.

Storage efficiency (%) =100 x (1 - overflow / inflow) provided that inflow<demand

System efficiency (%) = 100 x water used / water falling on the roof

In the dry season, a small tank may run dry, forcing users to seek water from alternative sources. Unreliability might be expressed as either the fraction of time (e.g. of days) when the tank is dry or the fraction of annual water use that has to be drawn from elsewhere. A RWH system may show unreliability not only because storage is small, but because the roof area is insufficient. Figure 4 shows how reliability, expressed as a fraction of year, varies with storage volume (expressed as a multiple of daily consumption) for two locations close to the Equator and therefore both with double rainy seasons.

Figure 4: Availability of rainwater supply as a fraction of the yearl

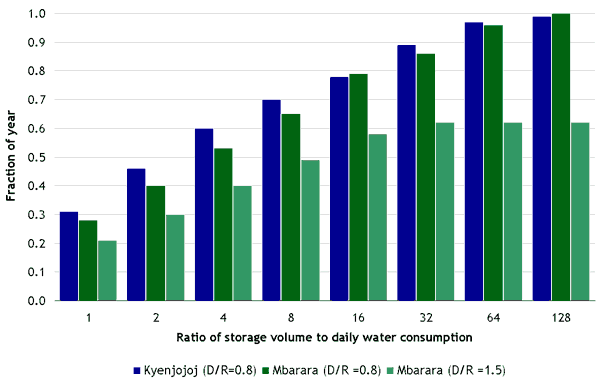
From this graph one can see that increasing storage size, and therefore cost, gives diminishing returns. For example look at the left hand column of each triplet (Kyenjojo with roof sized such that average annual water demand is only 80% of average annual roof runoff). Assuming a say 100 litres per day demand, shows that increasing storage from 1 day (100 l) to 16 days (1600 l) raises the reliability from 31% to 78%, but storage has to be increased as high as 128 days (12,800 l) to achieve 99% reliability. Such high reliability is so expensive that it is an unrealistic design objective for a DRW system in a poor country. In any case, as we shall see below, users may change behaviour so as to reduce the effective unreliability of their systems.

System features (that affect tank sizing)

• An oversize roof slightly extent compensates for an undersize tank. 
• If users are able and willing to adjust their consumption downwards during dry seasons, or when they find water levels in their tank lower than average, tanks can be sized smaller.
• ‘Partial’ RWH systems, either where it is accepted that RW will not meet needs throughout the year or where rainwater is only used to meet specific water needs like cooking/drinking, can be built with surprisingly small tanks.
• The reliability level appropriate to the design of a RWH system rises with the cost (in money, effort or even ill-health) of the alternative source that is used when the tank runs dry.

Rainfall data

Rainfall is very variable, especially where annual precipitation is less than 500mm. It also varies with location, so that data from a rain gauging station 20km away may be misleading when applied to the site of the RWH system. From the lowest to the highest quality of rainfall data we can think of at least 6 categories:

• No numerical data available, but of course local people know quite well the seasonality of precipitation and which crops will grow (with what sort of water-stress failure rate). 
• There is no numerical data, but RWH has been practised for long enough locally for people to have a feel for what is an adequate tank size.
• Only annual average rainfall is available, probably at a somewhat distant recording point, plus local knowledge of seasonality.
• Monthly rainfall, averaged over at least 4 years, can be obtained.
• Actual monthly rainfall records for at least 4 years, and preferably 7 years, are available for the site or for a location sufficiently nearby to give confidence or allow some systematic correction to be applied.
• Daily rainfall data for a relevant location and lasting at least 4 years is available.

Daily data is adequate for all design methods except perhaps the optimisation of gutters for which rainfall intensity data is useful (e.g. the fraction of annual precipitation falling at a rate faster than say 1mm per minute). Rainfall data can be expensive to purchase and is often hard to locate even where it exists. Obviously methods of sizing tanks that require as an input rainfall data of a sort that is not locally available should not be used.