The Vortex-Ring Facility:
Below is a technical drawing of the facility we have built on and around the large turntable. Then look at some PHOTOS AND VIDEOS . These show you how the setting up of the apparatus progressed since we started and the videos illustrate the motion of vortex rings.
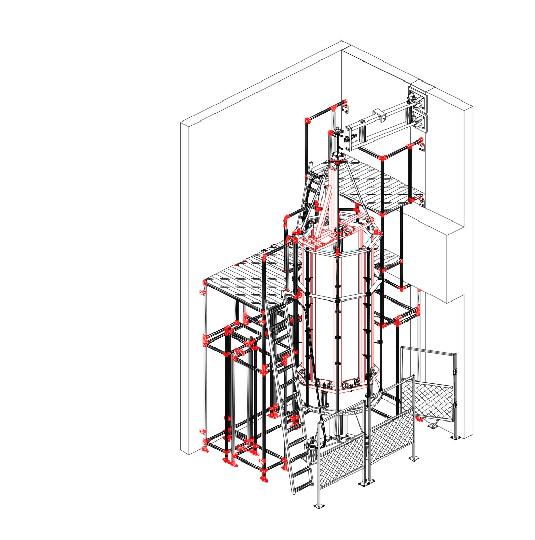
The centerpiece of the facility is the large turntable. The turntable supports a water-filled tank which is about 2.5 metres high and approximately 1 metre in 'diameter' (well,... the cross section of the tank is actually octagonal).
A standard piston-type vortex generator is mounted at the top of the facility. Those of you who are familiar with this technique will know what I mean; those who are not can look for instance at Maxworthy (1977, J.Fluid Mech. vol. 81, pp. 465-495) to see what I mean. A vortex ring is generated by when the piston pushes water out of the circular tube in which it is housed The diameter of the vortex-generator nozzle is presently 5 cm but we are building a second nozzle with a diameter of 15 cm. The piston motion and the motion of the rotating turntable are fully computer controlled.
Once generated the vortex ring then propagates vertically downwards through the water inside the tank. The axis of rotation coincides with the centre of the ring.
The whole facility is about 5.7 metres high. In order to get to the top of the tank to service the vortex generator we have built scaffolding around the turntable and the tank.
Why we are doing this? Vortices are the fundamental dynamical structures in fluid flows. As Kuecheman (1965, J.F.M. vol. 21, p.1) said they are the "sinews and muscles of fluid motion" OK, and why background rotation? The influence of background rotation is, for instance, of interest to all sorts of problems in geophysical fluid dynamics or flows in rotating machinery. So what!?... Well, the vortex rings are fully three-dimensional structures. Their motion conflicts with the Taylor-Proudman theorem which would like to keep the flow two-dimensional. The question is how does the system resolve this problem? How is the motion and the vortex stability affected by the presence of background rotation?
Return to Index