Willmore-DeTurck

We devised a fully discrete scheme for finding approximate solutions

$x : [0,T] \times S^1 \to \mathbb{R}^2, \qquad c : [0,T] \times S^1 \to \mathbb{R}, \qquad \lambda : [0,T] \to \mathbb{R}$

to the system of equations

$\nu \cdot \dot{x} = - k_s H + k_b \, (\Delta_\Gamma H + \tfrac{1}{2} H^3) + \lambda + f({c}),$ $\tau \cdot \dot{x} = \frac{1}{\alpha} \, \frac{x_p \cdot x_{pp}}{|x_p|^3},$ $\dot{c} = k_c \, \Delta_\Gamma {c} - {c} \, \nabla_\Gamma \cdot \dot{x} + \nabla_\Gamma \cdot (c \, \tau \, (\tau \cdot \dot{x})),$ $0 = \int_{S^1} \nu \cdot \dot{x} \, dp.$

Prior work. Several schemes for equations of this kind have been proposed in the literature, all of which introduce an auxiliary variable for the mean curvature $H$ determined using $H \nu = - \Delta_\Gamma x$ . This makes it difficult to impose the DeTurck tangential velocity and increases the computational effort.

Our approach. We instead propose to use the identity $H = - \frac{x_p^\perp \cdot x_{pp}}{|x_p|^3}$ and use $H^2$ -conforming finite elements to discretise the resulting fourth-order equation. Apart from avoiding auxiliary variables, this allows for fourth-order convergence in terms of the number of spatial degrees of freedom.
We use a semi-implicit time-stepping scheme which only requires the solution of linear systems. The downside of this approach is that it only yields first-order convergence.

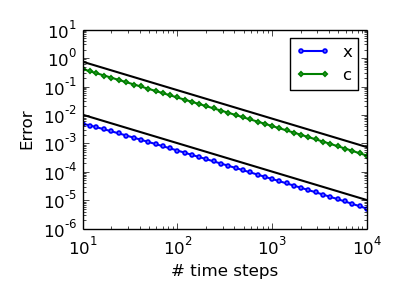
Assessing the DeTurck reparametrisation.

The following clips show the mesh evolution for two different values of $\alpha$ . The merits of the DeTurck reparametrisation (left series) compared to a purely normal flow (right series) are obvious.

$\alpha = 10^{-4}$
(strong tangential redistribution)

$\alpha = 10^{4}$
(virtually no tangential redistribution)