Saturation Height

Given the initial ground level ambient temperature T₀', initial air parcel temperature T₀ and the water vapour content of the moist air parcel, we would like to be able to say at what height in the atmosphere the water vapour starts condensing out. In order to do this we need to consider the different components making up the total pressure of the air parcel. The total atmospheric pressure is equal to the sum of the partial pressures of the individual gases, where the partial pressure is the pressure exerted by a gas in the mixture if it occupied the same volume as the mixture. This is know as Dalton's Law of partial pressure. If p_a is the total pressure of the air parcel then p_a = p_d + e where p_d is the partial pressure exerted by dry air and e is the partial pressure exerted by water vapour. We know that as the moist air parcel rises it expands in order to match the atmospheric pressure, and we assume that is does so instantly. Using a formula for the atmospheric pressure we therefore have the partial pressure of water vapour as a function of height (meters)

$e(z) = p_0 \left( 1 - \frac{\Gamma z}{T_0'} \right)^{\frac{gM}{R\Gamma}},$

The figure below shows how the water vapour pressure evolves with height. We now use a formula for the saturation pressure of water vapour, that is the maximum amount of pressure the water vapour can exert in the air parcel before the vapour starts condensing out into water droplets. We use the approximation for the saturation vapour pressure of water vapour over liquid in terms of temperature T derived from the Clausius-Clapeyron equation

$e_{s} = 611.2\exp \left( \frac{17.67(T-273.15)}{T - 29.65} \right).$

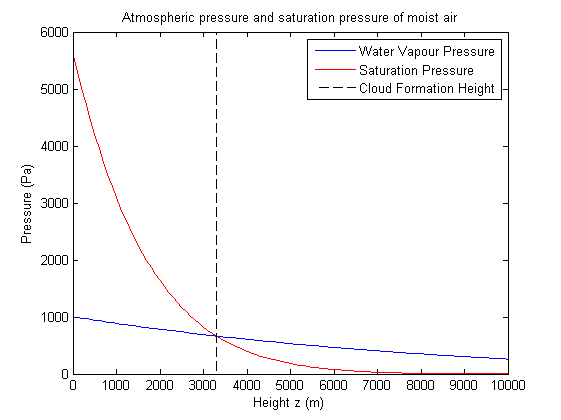
Saturation height

Here we have plotted the water vapour partial pressure and the saturation pressure. The intersection indicates the point at which water vapour begins to condense out. This graph uses an initial ground level ambient temperature of 15^oC, initial air parcel temperature of 35^oC and initial water vapour pressure of 1000Pa indicating a cloud will form at around 3300m. Condensation occurs if the vapour pressure is greater than or equal to the saturation pressure, ie. if the air parcel is at or above the cloud formation height.