The Frog Model

Introduction

Our group research project concerned an interacting particle system called the Frog Model (FM).

Intuitively, the FM over a graph $\mathcal{G}$ is described as follows: at each site of the graph itself there is a certain number of particles (which we will also call "frogs").

These particles are all sleeping, apart from those which lie at a single vertex of the graph, called the root.

At time 0, particles at the root begin to move in the graph performing a discrete simple random walk (SRW): each frog chooses a neighbouring site with uniform probability and moves to it.

Whenever a particle jumps to a place at which there are sleeping frogs, all these frogs are awakened and they follow the same dynamics described above; that is, they perform a SRW independently of all other frogs.

Moreover, there is the option to give each particle a finite lifetime (normally in the form of a geometric random variable) and when its life ends, the particle dies and stops moving.

One can place a deterministic or a random number of frogs at each vertex. We denote the number of frogs at each vertex by $\eta=\{\eta_x\}_{x\in\mathcal{G}}$

In the topic of random walks in random environments there are two probability measures we care about: quenched and annealed. The quenched measure is the one you get by first fixing the environment (in this case this is the initial configuration of frogs η) and then looking at what happens once the dynamics of the system are started. The annealed (or averaged) measure is the result of averaging the quenched measure over all possible starting configurations.

Linear Cover Times

We concerned ourselves with increasing subgraphs of $\mathcal{G}=\mathbb{Z}^d$ and the associated cover times.

The shape theorem for the frog model over $\mathbb{Z}^d$ tells us that the model explores the graph in a linear way; this is why we look for linear cover times. We created simulations in Python to confirm this:

The shape of the FM on a 2-d grid

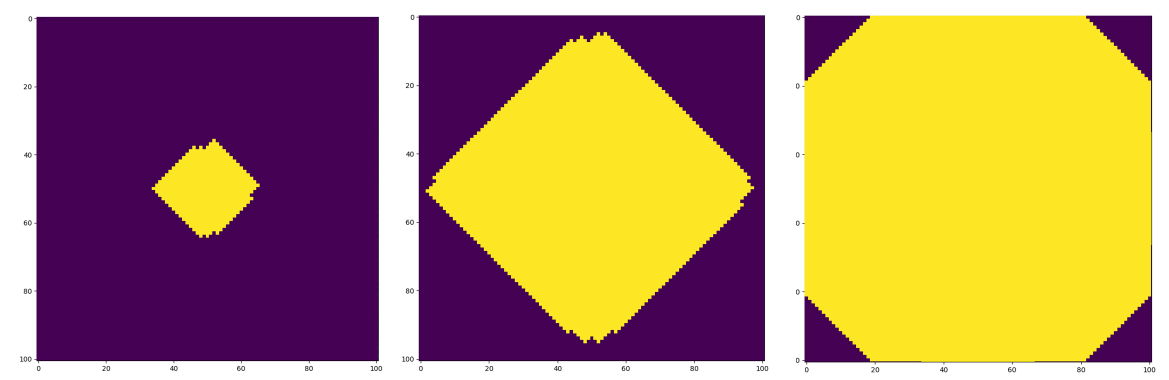
This picture shows how the explored area of the graph grows over time. Until the frogs reach the boundary, one may use the shape theorem to assert that the radius of this shape grows linearly with time. The shape theorem asserts the existence of an asymptotic shape $\mathcal{A}$ . If the distribution on η has a sufficiently heavy tail then this asymptotic shape is actually equal to the diamond $\mathcal{D}$ (equal to the circle of radius 1 under the manhattan metric). We also simulated this scenario and obtained the following pictures:

heavytailed

Letting $\mathbb{Q}$ denote the annealed measure, our result is the following:

Theorem:

Let A be an open and simply connected subset of $\mathcal{D}\subset\mathbb{R}^d$ that contains the origin and let $A_N := N \times A$ .

We consider the FM with initial configuration $\eta=\{\eta_x\}_{x\in A_N}$ with a heavy logarithmic tail. If $T_N$ denotes the time taken by this FM to cover $A_N$ then we have that
$\exists C^\ast > 0 \quad \text{such that} \quad \mathbb{Q}(T_N\leq C^\ast N)\longrightarrow 1,\text{ as }N\rightarrow\infty$ conditional on $\eta_0 >0$ .

This theorem confirms what the Shape Theorem suggests - that the FM explores subgraphs of $\mathbb{Z}^d$ at a linear speed. However, this is only a result in probability; a much more desirable result would be one in expectation. i.e. we would like to show that $\mathbb{E}_{\mathbb{Q}}\left[ T_N\right] =\mathcal{O}(N)\text{ as } N\rightarrow\infty$ .

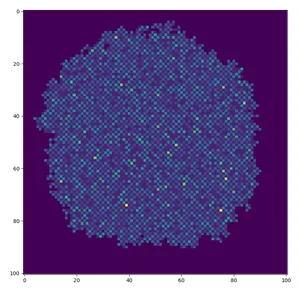
Here is a simulation of the FM on a 120x120 grid with one frog at every vertex:

The different colours indicate different numbers of frogs at each vertex.

References

[1] O. S. M. Alves, S. Y. Popov, and F. P. Machado. The shape theorem for the frog model. ArXiv Mathematics e-prints, February 2001.

[2] Serguei Yu Popov. Frogs and some other interacting random walks
models. In Discrete Random Walks, DRW'03, volume AC, pages 277-288. Discrete Mathematics and Theoretical Computer Science, 2003.

[3] O. S. M. Alves, S. Y. Popov, F. P. Machado, et al. Phase transition for the frog model. Electronic Journal of Probability, 7, 2002.

Acknowledgements

We would like to thank Elisabetta Candellero and David Croydon for their supervision. We also acknowledge EPSRC and the MASDOC CDT for their funding and support.