This page is under construction - bear with me, it will be finished soon! :)

My research interests are in applied analysis, with a focus on modelling and control of problems described by partial differential equations (PDEs) and with relevance to applications in the physical, life, and social sciences. The problems I work on usually involve an interplay between modelling, applied analysis and numerical simulations of PDEs and (systems of) ODEs or SDEs, often in multi-scale scenarios. Current projects include

• Control of interfacial flows using hierarchies of models
• Modelling and control for pedestrian dynamics (See a Warwick press release from when I participated in the STEM for Britain competition.)
• Modelling and control for opinion dynamics, usually on evolving social networks.

Here are links to my Google Scholar, ResearchGate and arXiv profiles.

See below for more detailed descriptions of each of my projects.

---

Control of falling liquid films

A thin liquid film falling down an inclined plane is a canonical setup in fluid dynamics which is relevant for many industrial applications. In some cases, such as coating, one wants the film to be perfectly smooth (or flat), while in others, such as heat and mass transfer, we want to drive the interface of these fluids to a travelling wave with a prescribed shape. My research focuses on developing controls that efficient and robust for these situations, based on a hierarchy of models.

Controls for falling liquid films can be passive or active. A passive control is prescribed a priori (e.g. at the beginning of an experiment or simulation) and it is not updated as the simulation evolves. Examples of this include a change on the topography of the plane, prescribed heating, adding a concentration of surfactants, etc. 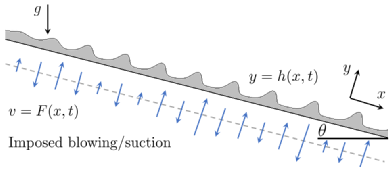On the other hand, an active control is designed based on the model and responds to changes in its evolution, and my research so far has focussed on controls actuated via blowing and suction of fluid through slots in the plane, responding to the interface height.

There is a well-known hierarchy of models that describe the interface of these flows:

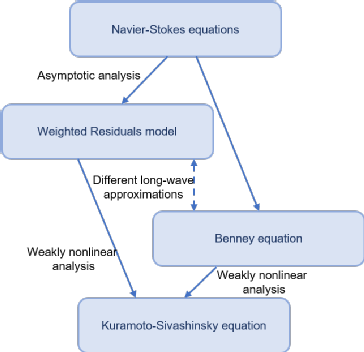
• The Navier-Stokes equations, the most detailed description of this phenomenon, where the controls appear as a boundary condition at the wall:
• Long wave models such as the Benney equation and the weighted residuals model, where the control appears as a right-hand side, but also as a nonlinear term. These models are based on an asymptotic assumption that the interface height is small compared to the domain length
• The Kuramoto-Sivashinsky (KS) equation, which is obtained via weakly nonlinear asymptotic analysis

During my PhD, I focused on designing controls for the KS equation, which is a fourth-order nonlinear parabolic PDE for the perturbation u to a flat interface :

This equation is the simplest example of an infinitely dimensional dynamical system that exhibits spatiotemporal chaotic behaviour, and therefore it has a large number of possible solutions. I designed controls that drive the solution of the KS equation to any desired unstable equilibrium. These are based on linear feedback control theory, i.e., they rely on stabilising the linear operator of the KS equation - and this can be proven to work for the nonlinear evolution using a Lyapunov-type argument.

I also showed that the controls are robust to uncertainties in the parameters of the equation, as well as to the inclusion of extra physical effects, such as dispersion, or destabilising electric fields.

These results were recently extended to a 2-dimensional KS equation in collaboration with Ruben Tomlin.

Still during my PhD, and in collaboration with Alice Thompson, we designed similar controls for the long-wave models in the hierarchy. We considered two equations: the Benney equation and the weighted-residuals model. Both equations are of the form, but the Benney equation gives an explicit formula for the flux while the weighted-residuals model couples it with a PDE for the flux, . We showed using linear stability analysis that control strengths that work for the Benney equation should also work for both the weighted-residuals model and the full Navier-Stokes equations, and confirmed this for the weighted-residuals model using extensive numerical simulations.

We tested distributed proportional controls - an unrealistic case where we would observe the interface everywhere and actuate the controls everywhere - but also point actuated controls based on observations of the full interface, as well as partial observations. We also discussed control not only towards a flat state but also towards any desired shape.

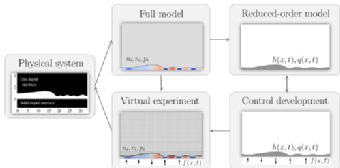More recently we performed the final step up in the hierarchy of models: testing the effectiveness of controls designed for the weighted residuals model in direct numerical simulations of the Navier-Stokes equations. We used direct numerical simulations (DNS) of the Navier-Stokes equations as a virtual experiment setting: this is a very computationally expensive setting, and therefore having analytical information from the reduced-order models is crucial. We showed that, even though the controls designed for the Benney and weighted-residuals model above are not directly applicable in the full setting (in the sense that we cannot just prescribe them as an "offline" type of control), we can use the feedback rules derived in the reduced-order models, with observations from the DNS, with almost as good results,

Over the years, I have worked on other problems 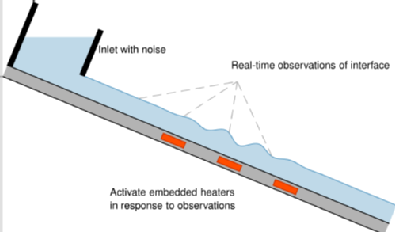related to falling liquid films. These include:

• the addition of noise to the equations (e.g., controlling the stochastic KS equation) which impacts not only falling liquid films but also combustion problems and ion sputtering processes). This also led to some interesting algorithmic issues related to T-Sylvester equations.
• Using other physical effects for control: heating the substrate, applying electric fields, ...

---

Modelling, inverse problems and control of pedestrian dynamics

Understanding the individual dynamics of pedestrians, as well as the collective behaviour of crowds is crucial for safety and transportation management, as it allows to predict what could happen in an evacuation, or to improve the design of rooms or buildings.

There are many models for pedestrian behaviour, ranging from microscopic (agent-based) models describing the behaviour of each pedestrian to macroscopic models which are PDEs that describe the collective motion of a large crowd. All these models are usually characterised using the fundamental diagram, which relates the observed density of pedestrians to their average velocity. Although there is a general agreement on the basic shape of this function, its parametrisation depends strongly on the measurement and averaging techniques used as well as the experimental setup considered.

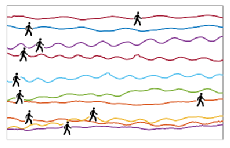
I use a coupling between agent-based and macroscopic models to estimate parameters in the fundamental diagram, in particular the maximum speed of a pedestrian, v_max, and the maximum density that pedestrians can walk through, ρ_max. The microscopic model describes the movement of each pedestrian and is an SDE of the form

The function F is given by the fundamental diagram and depends on the density ρ of pedestrians. Taking the mean-field limit, we know that the density solves a Fokker-Planck equation

I explore this coupling to find a likelihood function for this problem. This gives me the probability that a value of v_max or ρ_max is its true value given observations of a pedestrian trajectory. The trajectories used can be generated from the model, or obtained from experiments, such as the ones depicted in the figure above. Using this likelihood function, we can use optimisation methods, as well as Bayesian inverse problems techniques (such as MCMC) to estimate the desired parameters.

My current work concerns

(1) incorporate pedestrian trajectories from experiments, assuming that the fundamental diagram is linear,

(2) adapt the methodology for more realistic versions of the fundamental diagram

(3) use these models to control the movement of crowds using the location of obstacles and doors, or visual signs.

Most of my work in this project is in collaboration with Marie-Therese Wolfram and Andrew Stuart. The main methodology was recently published in

---

Mean-field limits of interacting particle systems

Summary

---

Optimal lockdown strategies for the COVID-19 pandemic in the UK

The current COVID-19 pandemic has caused whole countries to lockdown, with a huge effect on people’s lives and in the economy. Naturally, there are questions about how efficient this lockdown is, and increasing interest in how our country will reduce social distancing measures and eventually go back to normal.

In this project, we propose to answer some of these questions by using epidemiological models for the spread of COVID-19 in the UK, which are calibrated specifically to the UK population using Approximate Bayesian Computation (ABC) applying census data and the increasingly available data from the NHS, PHE and the ONS.

These models will then be explored in order to design an optimal mitigation strategy based on closing public and commercial venues, or shutting down transport links. Possible exit strategies from our lockdown will then be computed using model predictive control and will be adapted frequently in response to daily data.

This project is in collaboration with R. Dutta and D. Kalise and is funded by the EPSRC via the grant EP/V025899/1 COVID-19: Optimal Lockdown.

For more information check our dedicated website and our preprint:

Jump to:

Control of falling liquid films

Modelling and inverse problems for pedestrian dynamics

Mean-field limits for interacting particle systems

Optimal lockdown strategies for the COVID-19 pandemic in the UK