2020-21
Organiser: Susana Gomes
The Applied Maths Seminars are held on Fridays 12:00-13.00 on MS Teams. You can send a membership request via MS Teams or email susana dot gomes at warwick dot ac dot uk if you want to be added to the team. Once you have joined the team, you will receive an Outlook invitation to the seminar itself every week, and all you will have to do is join the meeting at the right time, either via the browser or app interface.
Please contact Susana Gomes if you have any speaker suggestions.
Seminar Etiquette:
- Please join the calls muted and without video, especially if late, to avoid interrupting and increase video quality.
- You will be added to the meeting as an attendee. This means you can't share screens but you should be able to share video and sound. If you want to ask a question during the presentation, you can either raise your hand or unmute yourself and ask it - just make sure you mute your microphone after.
- At the end of the talk, we will have oral questions as usual, and people can unmute themselves (and turn on their video).
- After the seminar, we will also stay around for virtual lunch and informal discussions.
Term 3
| Week | Date | Speaker | Title |
| 1 | 30 Apr |
Jessica Williams (MIT) Note 1pm start! |
The role of geometry in medicine (abstract) |
| 2 | 7 May | Denys Dutykh (CNRS) | A Hamiltonian regularization of shallow water waves (abstract) |
| 3 | 14 May | David Martinez (Warwick) | From a plasma physics problem to the bottomless rabbit hole of dynamical systems (abstract) |
| 4 | 21 May | Alexander Freidin (Institute for problems in mechanical engineering, Russia) |
Coupled problems of mechanochemistry: statements and solutions (abstract) |
| 5 | 28 May | Robert Nurnberg (Trento) | Variational approximation of axisymmetric mean curvature flow and surface diffusion (abstract) |
| 6 | 4 Jun | Virginie Ehrlacher (École des Ponts) | Moment constrained optimal transport problem: application to quantum chemistry (abstract) |
| 7 |
11 Jun |
Rachel Nicks (Nottingham) | Understanding Sensory Induced Hallucinations: From Neural Fields to Amplitude Equations (abstract) |
| 8 | 18 Jun | Malena Sabaté Landman (Bath) |
Flexible Krylov methods for inverse problems (abstract) |
| 9 | 25 Jun | Bjorn Stinner (Warwick) |
Modelling and Approximation of Cell Blebbing with Surface Finite Elements (abstract) |
| 10 | 2 Jul | Esther Daus (TU Wien) |
Cross-diffusion systems in biology: rigorous derivation, analysis and entropy structure (abstract) |
Term 2
| Week | Date | Speaker | Title |
| 1 | 15 Jan | Anastasia Borovykh (Imperial) | To interact or not? On the convergence properties of interacting particle optimization (abstract) |
| 2 | 22 Jan |
Richard Mann (Leeds) |
Collective decision-making by rational individuals (abstract) |
| 3 | 29 Jan | Stefan Klus (Surrey) | Data-driven analysis of complex dynamical systems (abstract) |
| 4 | 05 Feb | Artur Gower (Sheffield) |
Ultrasonic measurements without prior knowledge (abstract) |
| 5 | 12 Feb | Anna Seigal (Oxford) | Algebraic methods in statistics and data analysis (abstract) |
| 6 | 19 Feb | Cinzia Soresina (Graz, Austria) | Bifurcations in reaction-diffusion systems for competing species: fast-reaction and cross-diffusion (abstract) |
| 7 |
26 Feb |
Cameron Hall (Bristol) | Node-based approximation of contagion dynamics on networks (abstract) |
| 8 | 05 Mar | Jaroslav Fowkes (STFC) |
Developing improved optimization algorithms for ptychographic image reconstruction (abstract) |
| 9 | 12 Mar | Carolina Urzua Torres (Delft, Netherlands) |
A new approach to Space-Time Boundary Integral Equations for the Wave Equation (abstract) |
| 10 | 19 Mar | Anthea Monod (Imperial) | Topological Data Analysis of Database Representations for Information Retrieval (abstract) |
Term 1
| Week | Date | Speaker | Title |
| 1 | 09 Oct | Mikhail Poluektov (WMG) | Non-parametric models in a form of function trees and methods of their identification using experimental data (abstract) |
| 2 | 16 Oct | Matthew Hennessy (Oxford) | Mathematical modelling of phase separation in hydrogels (abstract) |
| 3 | 23 Oct | Josephine Evans (Warwick) | Existence of a non-equilibrium steady state for the non-linear BGK model on an interval (abstract) |
| 4 | 30 Oct | Stefan Engblom (Uppsala) | Computational Bayesian modeling for disease control (abstract) |
| 5 | 06 Nov | Rafael Bailo (Lille) |
Energy-Dissipating Schemes for Aggregation-Diffusion Gradient Flows (abstract) |
| 6 | 13 Nov | Elisa Davoli (TU Vienna) |
Nonlocal-to-local convergence of Cahn-Hilliard equations (abstract) |
| 7 |
20 Nov at 2pm |
Franziska Weber (Carnegie Melon) |
Note that this seminar starts at 2pm due to the time difference Numerical approximation of statistical solutions of hyperbolic systems of conservation laws |
| 8 | 27 Nov | Svetlana Dubinkina (CWI Amsterdam) | Shadowing approach to data assimilation (abstract) |
| 9 | 04 Dec | Bernhard Schmitzer (Goettingen) | Barycenters for the Hellinger-Kantorovich distance (abstract) |
| 10 | 11 Dec | Siri Chongchitnan (Warwick) | Cosmological inflation (abstract) |
Abstracts
Term 3
Week 1. Jessica Williams (MIT) - The role of geometry in medicine
Geometrical questions commonly arise in clinical practice: for example, what is the optimal shape for a particular medical device? or what shapes of anatomical structures are indicative of pathological events? In this talk we explore two disparate clinical applications of geometrical underpinning: (A) how to design the optimal device for kidney stone removal surgery? and (B) what blood vessel shapes are associated with biomechanical failure?
(A) Flexible ureteroscopy is a minimally invasive treatment for the removal of kidney stones by irrigating dust-like stone fragments with a saline solution. Finding the optimal ureteroscope tip shape for efficient flushing of stone fragments is a pertinent but complex question. We represent the renal pelvis (the main hollow cavity within the kidney) as a 2D
cavity and employ adjoint-based shape optimisation to identify tip geometries that shrink the size of recirculation zones thereby reducing stone washout times.
(B) The aorta is the largest blood vessel in the body, with an archetypal arched “candy-cane” shape and is responsible for transporting blood from the heart to the rest of the body. Aortic dissection, in which the inner layer of the aorta tears, can lead to frank rupture and is often rapidly fatal. Accurate clinical assessment of dissection risk from a CT scan of a patient’s thorax is paramount to patient survival. We apply statistical shape analysis, coupled with hemodynamic simulations, to identify pathological shape features of the aortic arch and to elucidate mechanistic underpinnings of aortic dissection.
Week 2. Denys Dutykh (CNRS) - A Hamiltonian regularization of shallow water waves
In this talk, I will demonstrate our approach towards constructing a slightly regularized version of the hyperbolic system of nonlinear shallow water equations. The particularity of our approach is that we succeed in regularizing solutions without introducing nor dispersion neither dissipation into governing equations. Moreover, the regularized system formally possesses the energy conservation law as long as a Hamiltonian formulation (though, a non-canonical one). The obtained system was shown to possess cusped travelling waves. The numerical behaviour and mathematical properties of the derived system will be highlighted within the limits of our current understanding. More precisely, the local well-posedness theory seems to be complete and the energy dissipation mechanism for weakly singular solutions seems to be equally understood. The latest developments over general (but smooth) bottoms will be presented as well. This work was done in collaboration with D. Clamond, D. Mitsotakis and R. Pego.
Week 3. David Martinez (Warwick) - From a plasma physics problem to the bottomless rabbit hole of dynamical systems
In the early 70’s O’Neil et. al. studied the problem of cold beam plasma interaction and proposed the so-called single wave model, a simple phenomenological PDE system that described the interaction very accurately. It was not until late 90’s until it was properly deduced from a standard plasma physics set of equations and shortly after the same author introduced a discrete version of the model in the form of an area-preserving map that corresponds to a high dimensional Hamiltonian mean-field coupled system.
The original idea was to use this map model to understand some key features of the original system, in particular the existence of coherent structures and transport barriers. However along the way, trying to use the dynamical system toolkit to give answers to physically relevant questions like: “do we have total mixing or not?”, it was necessary to reach a compromise between the questions, the literature and the development of new tools. While it may be too difficult to find answers or even write the questions for a self-consistent N+2 dimensional symplectic map, a reduced non-autonomous bidimensional tilt map can help us to understand things better. I will review the results in the literature close to the original problem and discuss in more detail the case of a non-autonomous standard map.
Week 4. Alexander Freidin (Institute for problems in mechanical engineering, Russia) - Coupled problems of mechanochemistry: statements and solutions
We consider chemical reactions between deformable solid and diffusing components. It is assumed that the reaction is localized at the reaction front and sustained by the diffusion of the diffusing reactant through the solid reaction product. The reaction is accompanied by transformation strains which produce mechanical stresses. Stresses in turn affect the reaction front velocity. We formulate coupled boundary value problems "diffusion-chemistry-mechanics" based on the concept of the chemical affinity tensor, according to which the stress-strain state affects the reaction front velocity through the normal component of the chemical affinity tensor. At first, a derivation of the chemical affinity tensor is given briefly. Then various models of the permeability of the reaction front with respect to the diffusing component are discussed. The examples of the solutions of the boundary value problems are given which demonstrate how the mechanical stresses can accelerate, retard and block the reaction front propagation. Finally, the stability of the reaction front is examined on the basis of the developed analytical procedure and numerical simulations of the front propagation. The competition between the macrokinetics of the reaction front and the local kinetics of the front perturbations far and near the front blocking position is discussed.
Week 5. Robert Nurnberg (Trento) - Variational approximation of axisymmetric mean curvature flow and
surface diffusion (joint work with John W. Barrett and Harald Garcke)
We present variational formulations of mean curvature flow and surface diffusion for axisymmetric hypersurfaces in R^3. On recalling important properties of the schemes introduced by the authors for the corresponding geometric evolution equations for closed curves in the plane, we introduce suitable finite element approximations, and investigate their stability and vertex distribution properties.
Week 6. Virginie Ehrlacher (École des Ponts) - Moment constrained optimal transport problem: application to quantum chemistry (joint work with A. Alfonsi, R. Coyaud and D. Lombardi)
The aim of this talk is to present some recent results on a relaxation of multi-marginal Kantorovich optimal transport problems with a view to the design of numerical schemes to approximate the exact optimal transport problem.
After a general introduction to Density Functional Theory and optimal transport problems, I will explain in this talk how the semi-classical limit of the so-called Lévy-Lieb functional, which is a central quantity in electronic structure computations, happens to be a symmetric multimarginal optimal tranport problem with Coulomb cost [1]. I will then present one particular numerical method which can be used for the resolution of such problem and avoids the curse of dimensionality. More precisely, the approximate problem considered consists in relaxing the marginal constraints into a finite number of moment constraints, while the state space remains unchanged (typically a subset of R^d for some positive integer d). Using Tchakhaloff’s theorem, it is possible to prove the existence of minimizers of this relaxed problem and characterize them as discrete measures charging a number of points which scales at most linearly with the number of marginals in the problem. In the particular case of a symmetric multi-marginal problem, like the Coulomb cost optimal transport problem arising in quantum chemistry applications, the number of points charged by minimizes is independent of the number of electrons, thus avoiding the curse of dimensionality. This result is strongly linked to the work [2] and opens the way to the design of new numerical schemes exploiting the structure of these minimizers. Some preliminary numerical results exploiting this structure will be presented.
[1] COTAR, Codina, FRIESECKE, Gero, et KLÜPPELBERG, Claudia. Smoothing of transport plans with fixed marginals and rigorous semiclassical limit of the Hohenberg–Kohn functional. Archive for Rational Mechanics and Analysis, 2018, vol. 228, no 3,, p.891-922.
[2] FRIESECKE, Gero et VÖGLER, Daniela. Breaking the curse of dimension in multi-marginal kantorovich optimal transport on finite state spaces. SIAM Journal on Mathematical Analysis, 2018, vol. 50, no 4, p. 3996-4019.
Week 7. Rachel Nicks (Nottingham) - Understanding Sensory Induced Hallucinations: From Neural Fields to Amplitude Equations
Explorations of visual hallucinations, and in particular those of Billock and Tsou [Neural interactions between flicker-induced self-organized visual hallucinations and physical stimuli. Proceedings of the National Academy of Sciences, 104(20):8490-8495, 2007], show that annular rings with a background flicker can induce visual hallucinations in humans that take the form of radial fan shapes. The well-known retino-cortical map tells us that the corresponding patterns of neural activity in the primary visual cortex for rings and arms in the retina are orthogonal stripe patterns. The implication is that cortical forcing by spatially periodic input can excite orthogonal modes of neural activity. Here we show that a simple scalar neural field model of primary visual cortex with state-dependent spatial forcing is capable of modelling this phenomenon. Moreover, we show that this occurs most robustly when the spatial forcing has a 2:1 resonance with modes that would otherwise be excited by a Turing instability. By utilising a weakly nonlinear multiple-scales analysis we determine the relevant amplitude equations for uncovering the parameter regimes which favour the excitation of patterns orthogonal to sensory drive. In combination with direct numerical simulations, we use this approach to shed further light on the original psychophysical observations of Billock and Tsou.
Week 8. Malena Sabaté Landman (Bath) - Flexible Krylov methods for inverse problems
Krylov subspace methods are powerful iterative solvers for large-scale linear inverse problems, such as those arising in image deblurring and computed tomography. In this talk I will give a brief introduction to Krylov methods, and flexible Krylov methods, and their interplay with Tikhonov regularization. Moreover, I will present two new algorithms to efficiently solve regularized problems that enforce sparsity in the solution. The performance of the algorithms will be shown through numerical examples. This is a joint work with Silvia Gazzola (University of Bath) and James Nagy (Emory University).
Week 9. Bjorn Stinner (Warwick) - Modelling and Approximation of Cell Blebbing with Surface Finite Elements
Joint work with Adam Nixon and Andreas Dedner.
Cell blebbing refers to the detachment of a cell's membrane from its main structural body and the formation of a protrusion. The process involves mechanical and biochemical aspects, details of which are only partially understood. Focussing on the initiation and the role of the cell geometry in triggering blebbing, a continuum approach leads to a parabolic fourth order partial differential equation for a surface representing the membrane position. We analyse a finite element approximation based on triangulated surfaces and a mixed approach involving operator splitting, and use it to show well-posedness of an initial value problem for the surface equation. Subject to suitable regularity, optimal error estimates can be derived. A high-level language facilitates a convenient implementation within a flexible, extensible framework whilst using efficient software backends. We report on computations to validate the theoretical results and on results for model extensions that account for membrane-bound biochemistry. Finally, we look into some preliminary results for an intrinsic approach to the problem where the computations are performed on an evolving triangulated surface rather than on a reference surface.
Week 10. Esther Daus (TU Wien) - Cross-diffusion systems in biology: rigorous derivation, analysis and entropy structure
In this talk I will present some recent results concerning the existence analysis of cross-diffusion systems in population dynamics and in biofilm growth models using entropy methods. I will further discuss how to derive these systems from stochastic many-particle systems and from a reversible Markov chain model. The equations are strongly coupled and the diffusion matrix is in general neither symmetric nor positive definite, furthermore, we can also treat degenerate, singular and non-local effects.
Term 2
Week 1. Anastasia Borovykh (Imperial) - To interact or not? On the convergence properties of interacting particle optimization
A good machine learning model can be characterized by i) convergence (close) to the optimum, ii) good generalization performance. The conventional way of optimizing is to run one instance of an optimizer. The question we address here is whether it is beneficial to run multiple instances, or particles, and allow these to interact. Working in the general context of stochastic mirror descent, we present convergence results which show that by controlling the interaction the variance of stochastic gradients can be reduced. At the same time interactions can help in converging to flatter minima which have been shown to generalize better.
Week 2. Richard Mann (Leeds) - Collective decision-making by rational individuals
Collective behaviours provide some of the most dramatic spectacles in nature, and some of the most dangerous in human societies. From swooping bird flocks and swirling balls of fish, to stock market crashes and crowd disasters, these phenomena are driven by interactions between individuals; following others, learning from their choices, and trying to survive and prosper in a social context. Mathematical models are crucial for understanding how individual interactions scale up to form group behaviours, but what are these interactions and where do they come from? In recent years much work has been done to uncover the precise rules governing how individual interactions empirically. Another approach, which I will describe here, is to develop “normative” models of behaviour, identifying the behaviours that theoretically optimise utility or fitness. Using a normative model of collective decision making I will show how key features of experimental data are consistent with animals maximising their expected utility based on social and private information. I will explore how ecological differences explain variation between animal species, and why animals may exhibit different social behaviour in the laboratory and the wild. I will also show why a normative, theory-driven approach is an essential companion to data-driven discovery of behavioural rules, and I will argue that “model-free” inference is a myth.
Week 3. Stefan Klus (Surrey) - Data-driven analysis of complex dynamical systems
Over the last years, numerical methods for the analysis of large data sets have gained a lot of attention. Recently, different purely data-driven methods have been proposed which enable the user to extract relevant information about the global behavior of the underlying dynamical system, to identify low-order dynamics, and to compute finite-dimensional approximations of transfer operators associated with the system. However, due to the curse of dimensionality, analyzing high-dimensional systems is often infeasible using conventional methods since the amount of memory required to compute and store the results grows exponentially with the size of the system. We extend transfer operator theory to reproducing kernel Hilbert spaces and show that these operators are related to Hilbert space representations of conditional distributions, known as conditional mean embeddings in the machine learning community. One main benefit of the presented kernel-based approaches is that these methods can be applied to any domain where a similarity measure given by a kernel is available. We illustrate the results with the aid of guiding examples and highlight potential applications in molecular dynamics, fluid dynamics, and quantum mechanics.
Week 4. Artur Gower (Sheffield) - Ultrasonic measurements without prior knowledge
Elastic and acoustic waves are in many ways ideal to probe materials: they travel with ease in most solids, easy to generate, and are safe for humans and for the material (in contrast to say X-rays or drilling holes). The figure below illustrates how to measure the stress σ1 in a solid plate by using elastic shear waves. We can estimate the stress from the time it takes for the shear wave to travel across the plate, because the higher the stress, the faster the shear wave will travel.
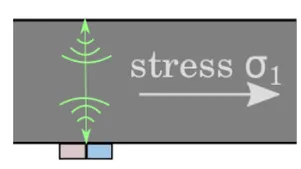 Despite these advantages, there is a significant drawback: to interpret the measurements, you often need to already know many elastic constants. For example, the higher the Young’s modulus the faster the waves travel, irrespective of the stress.
Despite these advantages, there is a significant drawback: to interpret the measurements, you often need to already know many elastic constants. For example, the higher the Young’s modulus the faster the waves travel, irrespective of the stress.
In this talk, I will show how we can use universal relationships between stress and strain to design measurements which do not need this prior knowledge of the materials elastic constants. Although I will focus on measuring stress, some of these tricks translate to designing other measurements for anisotropic materials.
Week 5. Anna Seigal (Oxford) - Algebraic methods in statistics and data analysis
Algebraic structure is at the heart of many problems in statistics and data analysis. We aim to fit data to a model, or to approximate data by a point on some locus of interest. I will discuss how algebraic structure can be used to capture the existence and uniqueness of a solution to these problems, as well as to suggest suitable algorithms. I will first consider parameter estimation in statistical models via maximum likelihood estimation. We will see connections between maximum likelihood estimation and invariant theory. I will then discuss tensors, the higher dimensional analogues of matrices. The loci of tensors that are of interest in applications often define semi-algebraic sets, given by polynomial equations and inequalities. One example is the signature, tensors that can be used to encode a path of time series data. We will see the algebraic structure that relates a path to its signature.
Week 6. Cinzia Soresina (Graz) - Bifurcations in reaction-diffusion systems for competing species: fast-reaction and cross-diffusion
The Shigesada-Kawasaki-Teramoto model (SKT) was proposed to account for stable inhomogeneous steady states exhibiting spatial segregation, which describes a situation of coexistence of two competing species. Even though the reaction part does not present the activator-inhibitor structure, the cross-diffusion terms are the key ingredient for the appearance of spatial patterns. We provide a deeper understanding of the conditions required on both the cross-diffusion and the reaction coefficients for non-homogeneous steady states to exist, by combining a detailed linearised analysis with advanced numerical bifurcation methods via the continuation software pde2path. We report some numerical experiments suggesting that, when cross-diffusion is taken into account, there exist positive and stable non-homogeneous steady states outside of the range of parameters for which the coexistence homogeneous steady state is positive. In 1D and 2D, we pay particular attention to the fast-reaction limit by computing sequences of bifurcation diagrams as the time-scale separation parameter tends to zero. We show that the bifurcation diagram undergoes major deformations once the fast-reaction systems limit onto the cross-diffusion singular limit. Furthermore, in 2D we find evidence for time-periodic solutions by detecting Hopf bifurcations, we characterise several regions of multi-stability and improve our understanding of the shape of patterns.
Week 7. Cameron Hall (Bristol) - Node-based approximation of contagion dynamics on networks
Contagion models on networks can be used to describe the spread of information, rumours, opinions, and diseases through a population. In the simplest contagion models, each node represents an individual that can be in one of a number of states (e.g. Susceptible, Infected, or Recovered), and the states of the nodes evolve according to specified rules. Even with simple Markovian models of transmission and recovery, it can be challenging to compute the dynamics of contagion on large networks: running simulations can be slow, and the system of master equations is typically too large to be tractable.
One approach to approximating contagion dynamics is to assume that each node state is independent of the neighbouring node states; this leads to a system of ODEs for the node state probabilities (the “first-order approximation”) that always overestimates the speed of infection spread. This approach can be made more sophisticated by introducing pair approximations or higher-order moment closures, but this dramatically increases the size of the system and slows computation. In this talk, I will present some alternative node-based approximations for contagion dynamics. The first of these is exact on trees with a single source of infection but will always underestimate the speed of infection spread on a network with loops. I will show how this can be combined with the classic first-order node-based approximation to obtain a node-based approximation that has similar accuracy to the pair approximation in some circumstances, but which is considerably faster to solve.
Week 8. Jaroslav Fowkes (STFC) - Developing improved optimization algorithms for ptychographic image reconstruction
In this talk I will present some recent work that we have been doing in STFC on developing improved optimization algorithms for the ptychographic reconstruction of images. STFC manages some of the country’s largest scientific facilities, including the diamond light source synchrotron which, amongst other things, is used for the microscopic imaging of scientific samples. One such recent imaging technique is ptychography, where a beam scans a sample and generates a set of diffraction patterns, which are then used to solve an inverse problem that reconstructs the image. The form of this inverse problem is particularly amenable to optimization and in this talk I will discuss in detail the optimization algorithms that we have been developing for this purpose, and how they compare to the existing techniques currently employed by physicists to solve the inverse problem in practice.
Week 9. Carolina Urzua Torres (TU Delft) - A new approach to Space-Time Boundary Integral Equations for the Wave Equation
Space-time discretization methods are becoming increasingly popular, since they allow adaptivity in space and time simultaneously, and can use parallel iterative solution strategies for time-dependent problems. However, in order to exploit these advantages, one needs to have a complete numerical analysis of the corresponding Galerkin methods.
Different strategies have been used to derive variational methods for the time domain boundary integral equations for the wave equation. The more established and succesful ones include weak formulations based on the Laplace transform, and also time-space energetic variational formulations. However, their corresponding numerical analyses are still incomplete and present difficulties that are hard to overcome, if possible at all.
As an alternative, we pursue a new approach to formulate the boundary integral equations for the wave equation, which aims to provide the missing mathematical analysis for space-time boundary element methods.
In this talk, I will give a short introduction to boundary element methods; briefly explain the current formulations for the wave equation; and finally discuss the new approach.
Week 10. Anthea Monod (Imperial) - Topological Data Analysis of Database Representations for Information Retrieval
Appropriately representing elements in a database so that queries may be accurately matched is a central task in information retrieval. This has recently been achieved by embedding the graphical structure of the database into a manifold so that the hierarchy is preserved. Persistent homology provides a rigorous characterization for the database topology in terms of both its hierarchy and connectivity structure. We compute persistent homology on a variety of datasets and show that some commonly used embeddings fail to preserve the connectivity. Moreover, we show that embeddings which successfully retain the database topology coincide in persistent homology. We introduce the dilation-invariant bottleneck distance to capture this effect, which addresses metric distortion on manifolds. We use it to show that distances between topology-preserving embeddings of databases are small. Joint work with Athanasios Vlontzos, Yueqi Cao, Luca Schmidtke and Bernhard Kainz.
Term 1
Week 1. Mikhail Poluetkov (WMG) - Non-parametric models in a form of function trees and methods of their identification using experimental data
This talk introduces a conceptually novel approach to data modelling. The data is considered to be a set of approximately known records of a physically deterministic system, where the output is assumed to be a result of the multiple inputs. The model is sought as a composition of multiple functions of one variable (a function tree), which is an equivalent replacement of a continuous multivariate function and is known as the Kolmogorov-Arnold representation. Furthermore, the model is non-parametric, which implies that the shapes of the involved functions are directly determined in the process of identification.
The foundation of the suggested algorithm is the identification of the kernel of the Urysohn operator (a non-linear integral operator), using known inputs and outputs of the operator. Such identification can be classified as solving an inverse problem for the integral equation of the Urysohn type. This basic method is then generalised to a composition of the Uryshon operators in a discrete form, with “hidden” intermediate variables, which constitutes the Kolmogorov-Arnold representation.
Week 2. Matthew Hennessy (Oxford) - Mathematical modelling of phase separation in hydrogels
A hydrogel is a soft, two-phase system consisting of a deformable solid matrix that is swollen with fluid. Slightly altering the temperature or pH of the surrounding environment can trigger the spontaneous formation of structures within and on the surface of the gel. This process, called phase separation, is of fundamental importance to materials science and cell biology due to its relevance in smart materials and neurodegenerative diseases. In this talk, I will discuss a flexible framework for deriving phase-field models of hydrogels using non-equilibrium thermodynamics. Numerical simulations and phase-plane analyses will be used to explore the wealth of scenarios that occur when a hydrogel undergoes phase separation. These include the propagation of fronts that destabilise and then rupture, and the formation of highly localised, highly swollen phases that are ejected from the free boundary of the gel one by one. Asymptotic methods will then be used to examine the electric double layer that forms at the interface between a polyelectrolyte gel and solvent bath. Phase transitions can lead to double layers with finite thickness or periodic structures while producing large compressive stresses that may result in instability. The talk will conclude with a discussion of viscoelastic and granular materials and current challenges in this area.
Week 3. Josephine Evans (Warwick) - Existence of a non-equilibrium steady state for the non-linear BGK model on an interval.
The BGK (Bhatnagar, Gross and Crook) equation models the behaviour of a dilute gas. It is similar to but simpler than the Boltzmann equation. We study the BGK equation where the space variable is in an interval with boundary walls which are heated to different temperatures. We show the existence of a non-equilibrium steady state for this equation when the boundary temperatures are large. I will discuss our results and also the interest of non-equilibrium steady states for non-linear gas equations and the challenges related to their analysis.
Week 4. Stefan Engblom (Uppsala) - Computational Bayesian modeling for disease control
Data-driven disease modeling and prediction are currently under intense pressure to deliver answers on a wide array of questions. In this talk I will therefore present work on Bayesian modeling of disease spread at national scales.
I first consider an endemic situation, namely the spread of shiga toxin-producing E. coli in Swedish cattle, and for which we have data over extended periods of time: this includes sample disease measurements (prevalence estimates), as well as a detailed transport network over about 10 years. The measurements are low-informative on the epidemiological state and distributed sparsely in both space and time. Nevertheless, we develop a Bayesian simulation-driven approach which performs convincingly, thus producing an in silico replica of the disease with predictive value. Some of the efforts that went into judging the identifiability and robustness of the overall procedure will be detailed, as well as tentative applications towards disease control.
I will conclude by highlighting an ongoing modeling effort concerning the Covid-19 situation in Sweden. The aim is to make use of several different data sources and produce predictions for the demands on hospitals, for early detection of hot-spots, and provide insight on the effectiveness of mitigation measures.
Co-authors: Samuel Bronstein (ENS Paris), Robin Eriksson, Alexander Medvedev, and Håkan Runvik (Department
of Information Technology, Uppsala University, Sweden), Stefan Widgren (Department of Disease Control and epidemiology, National Veterinary Institute, Sweden)
Week 5. Rafael Bailo (Lille) - Energy-Dissipating Schemes for Aggregation-Diffusion Gradient Flows
We propose fully-discrete, implicit-in-time finite-volume schemes for general non-linear non-local Fokker-Planck equations with a gradient flow structure. The schemes verify the positivity-preserving and energy-dissipating properties, done conditionally by the second order scheme and unconditionally by the first order counterpart. Dimensional splitting allows for the construction of these schemes with the same properties and a reduced computational cost in any dimension. We will showcase the handling of complicated phenomena: free boundaries, meta-stability, merging, and phase transitions.
Week 6. Elisa Davoli (TU Vienna) - Nonlocal-to-local convergence of Cahn-Hilliard equations
In this talk, we will consider a class of nonlocal viscous Cahn-Hilliard equations with Neumann boundary conditions for the chemical potential. The double-well potential will be allowed to be singular (e.g. of logarithmic type), while the singularity of the convolution kernel will not fall in any available existence theory under Neumann boundary conditions. We will prove well-posedness for the nonlocal equation in a suitable variational sense. Secondly, we will show that the solutions to the nonlocal equation converge to the corresponding solutions to the local equation, as the convolution kernels approximate a Dirac delta. The asymptotic behavior will be analyzed by means of monotone analysis and Gamma-convergence results, both when the limiting local Cahn-Hilliard equation is of viscous type and of pure type. This is based on a series of joint works with H. Ranetbauer, L. Scarpa, and L. Trussardi.
Week 7. Franziska Weber (Carnegie Melon) - Numerical approximation of statistical solutions of hyperbolic systems of conservation laws
Statistical solutions are time-parameterized probability measures on spaces of integrable functions, which have been proposed recently as a framework for global solutions for multi-dimensional hyperbolic systems of conservation laws. We present a numerical algorithm to approximate statistical solutions of conservation laws and show that under the assumption of 'weak statistical scaling', which is inspired by Kolmogorov's 1941 turbulence theory, the approximations converge in an appropriate topology to statistical solutions. Numerical experiments indicate that the assumption might hold true in practice.
Week 8. Svetlana Dubinkina (CWI Amsterdam) - Shadowing approach to data assimilation
Data assimilation is broadly used in atmosphere and ocean science to correct error in the state estimation by incorporating information from measurements (e.g. satellites) into the mathematical model. The widely-used variational data assimilation method has a drawback of a drastic increase of the number of local minima of the corresponding cost function as the number of measurements increases. The shadowing approach to data assimilation, which was pioneered by K. Judd and L. Smith in Physica D (2001), aims at estimating the whole trajectory at once. It has no drawback of several local minima. However, it is computationally expensive, requires measurements of the whole trajectory, and has an infinite subspace of solutions.
We propose to decrease the computational cost by projecting the shadowing approach to the unstable subspace that typically has much lower dimension than the phase space. Furthermore, we propose a novel shadowing-based data assimilation method that lifts up the requirement of a fully-observed state. We prove convergence of the method and demonstrate in numerical experiments with Lorenz models that the developed data assimilation method substantially outperforms the variational data assimilation method.
Week 9. Bernhard Schmitzer (Goettingen) - Barycenters for the Hellinger-Kantorovich distance
The Hellinger--Kantorovich metric is an unbalanced generalization of the Wasserstein distance, allowing the comparison of non-negative measures of arbitrary mass. The Wasserstein barycenter is a geometrically
intuitive way to form an average between probability measures. In this talk we study the barycenter of the Hellinger--Kantorovich metric. We find that it differs substantially from the Wasserstein barycenter by exhibiting a local clustering behaviour that depends on the length scale of the input measures.
Joint work with Gero Friesecke and Daniel Matthes.
Preprint: https://arxiv.org/abs/1910.14572
Week 10. Siri Chongchitnan (Warwick) - Cosmological inflation
How do cosmologists model the early Universe? In this non-specialist talk, I will give an introduction to the leading theory of the early Universe known as cosmological inflation, which postulates a brief period of exponential cosmic expansion 13.8 billion years ago. I will explain why inflation is needed, and give some insights into its mathematical details. I will describe some unsolved problems in inflation, and describe how future experiments (such as space-based gravitational-wave satellites) could constrain and rule out competing inflation models, hence giving new insights into the origin of the Universe.
