H2@C60

The union of the simplest molecule (H₂) and the most symmetric molecule (C₆₀) known to men have enabled the observation of quantum mechanics at a molecular level. The truncated icosahedral symmetry of the C₆₀ cage enable the guest molecule to behave like a three-dimensional quantum harmonic oscillator.

Due to symmetry requirements, para-H₂ can only be in states where its rotational angular momentum quantum number, j, is even (0, 2, 4 ...), while ortho-H₂ can only have odd j (1, 3, 5 ...). Inter-conversion between the two species is slow in the absence of catalyst as most typical intra-molecular interactions that causes spin flip are small and the energy difference between the rotational energy levels is large because interaction must flip space and spin states simultaneously. [1]

The dynamics of the hydrogen can be described in terms of 5 quantum numbers (ν, j, n, l, λ, m). The quantum number ν =0, 1… represents vibration, while j is as above, represents the rotation of the hydrogen molecule. The integer n is the principle quantum number that describes the displacement of the centre of mass of the hydrogen molecule from the centre of the cage. The quantum number l on the other hand, expresses the hydrogen molecule's translational angular momentum. This integer can only assume a positive value and is defined as l = n, n-2… until 1 or 0 depending if n is odd or even. λ is the quantum number that describes the vector sum of translation and rotational angular momentum, $\Lambda = L + J$ , where $|L|=\hbar \sqrt{l(l+1)}$ and $|J|=\hbar \sqrt{j(j+1)}$ . [1][2] The quantum number m is the projection of the total angular momentum along any quantization axis and it can take integer values from -λ to λ [2]. However, in isotropic systems such as H₂@C₆₀, m is not a good quantum number due to the translational-rotational (TR) coupling. λ is the better quantum number as it is used to clarify the TR coupled states.

The energy of the H₂ molecules can be written as:

$E(\nu, j ,n, \lambda) = (v +\frac{1}{2}) \omega_\nu) + (n +\frac{3}{2}) \omega_n) + B_\nu j(j+1) + c(l, j, \lambda) V_{t-r}$ (Equation 1)

where $\hbar$ is the reduced Planck constant, $\omega_\nu$ is the vibrational quantum of energy, $\omega_n$ is the translational quantum of energy. $B_\nu = B_e - \alpha_e (\nu+\frac{1}{2})$ is the rotational constant with $\alpha_e$ representing the vibration-rotation (VR) correction. The last term represents the TR coupling that is responsible for the sub-level splitting, where $V_{t-r}$ is the TR coupling and $c(l, j, \lambda)$ is the coefficient. The results from the above equation can be plotted in an energy level diagram (Figure 1). The degeneracy of the energy levels in Equation 1 is expressed in terms of $g=2\lambda+1$ .

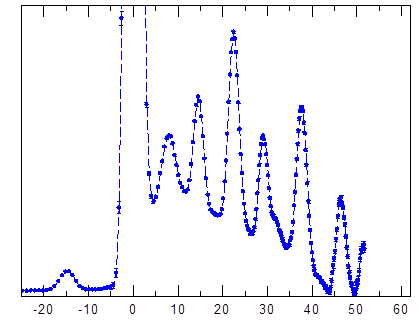
H2@C60 INS

Figure 1. The inelastic neutron scattering (INS) spectrum of the H2@C60 at 1.5K.

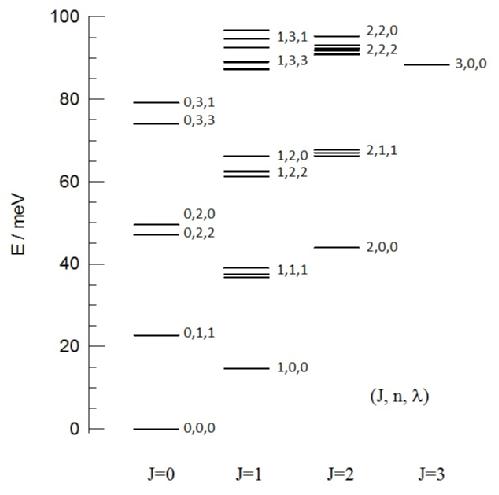
H2@C60 Energy levels

Figure 2. Energy levels of H₂@C₆₀ as observed from inelastic neutron scattering (INS) spectroscopy (see Figure 1). The numbers next to each energy level represents their respective quantum numbers, J, n and λ.

References:
1. A. J. Horsewill, K. S. Panesar, S. Rols, J. Ollivier, M. R. Johnson, M. Carravetta, S. Mamone, M. H. Levitt,Y. Murata, K. Komatsu, J. Y.-C. Chen, J. A. Johnson, X. Lei, and N. J. Turro (2012) Phys. Rev. B 85, 205440.
2. M. Xu, F. Sebastianelli, Z. Bacic, R. Lawler, and N. J. Turro. Quantum dynamics of coupled translational and rotational motions of H2 inside C60 (2008) J. Chem. Phys, 128:011101.