Skip to main content Skip to navigation

Integrated Magnetic Resonance Centre for Doctoral Training

H2@C70

Unlike the H2@C60, the H2@C70 consists of a C70 fullerene that acts as a cage for the trapped H2 molecule. Otherwise, the H2@C70 shares the same physical properties as the H2@C60, its elegant and more symmetric variant of endofullerenes. The C70 cage consistsof 70 carbon atoms arranged in an ellipsoidal shape resembling a rugby ball, with point group symmetry D5h. [1] Hence, the C70 cage is anisotropic as one of its axes is longer than the other two.

The cage potential of C70 experienced by the trapped H2 has been calculated using 5D Potential Energy Surface constructed by summing over pairwise interactions of each atom of H2 with each atom of C60 (Figure1). The H-C interactions are modelled using the standard Leonard-Jones potential. [2] From 1, we can see that the cage potential of the long axis is highly anharmonic and seems almost flat in the central region, whereas the other two short axes cages potential are similar to the cage potentials in H2@C60. [2] Therefore, the C70 has cage potentials resembling a square-well potential on the long axis, and harmonic potentials on the other two short axes.

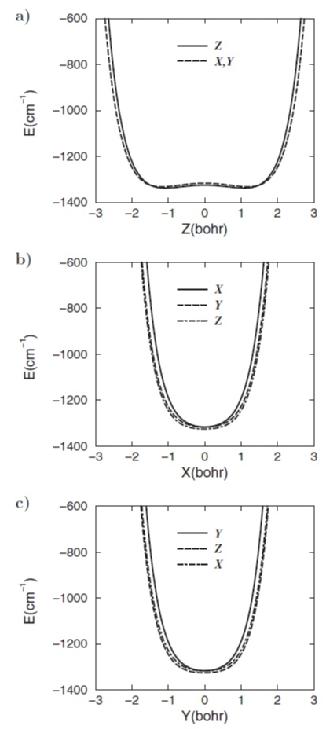
C:\Users\ppxkg\Dropbox\Endofullerenes\H2@C70\Documents\C70 cage potential.jpg

Figure 1.The above illustrates the 1D cut through of the optimized 5D Potential Energy Surface of H2@C70. The legends on the graphs represent the orientations of the H2 relative to the C70 at the time of the calculations, where Z is for H2 aligned with the long axis (z), while X and Y are for H2 aligned with the short axes (x and y). [2]

The lower symmetry of the C70 cage causes splitting in states which are otherwise degenerate in H2@C60. [1, 2] For example, the J =1 ground states of ortho-H2, which is triply degenerate in the case of H2@C60, is split in the case of H2@C70 into a non-degenerate state with the rotating H2 longitudinally polarized with respect to the C70 long axis (A2” symmetric level), and a doubly degenerate state with the rotating H2 transversely polarized with respect to the C70 long axis (E1’ symmetric level). [1] The spatial wavefunction of H2 in the A2” state has the form of a pz atomic orbital oriented along the long axis of the cage, whereas the spatial wavefunctions of the degenerate E1’ states may be represented either as transverse px and py orbitals, or as a complex superposition of both orbitals, giving rise to torus-like complex wavefunctions (see Figure 2). [1]

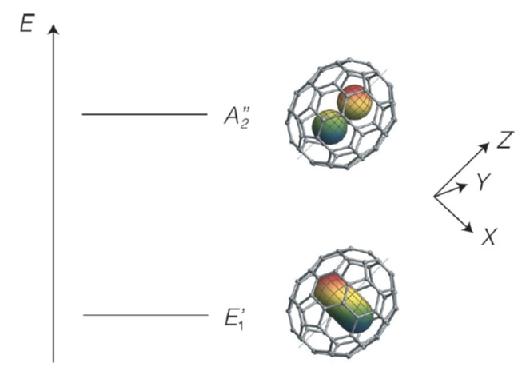
C:\Users\ppxkg\Dropbox\Endofullerenes\H2@C70\Documents\H2@C70 ground state wave function.jpg

Figure 2. The figureabove illustrates the spatial wavefunctions of the two lowest energy levels of ortho-H2. The labels A2” and E1’rrepresents the symmetric levels of their respective states. The wavefunctions of the confined hydrogen are represented by the torus-shaped and pz-shaped orbitals inside the fullerene respectively. [1]



References

  1. Salvatore Mamone, Maria Concistr, Ivo Heinmaa, Marina Carravetta, Ilya Kuprov, Gary Wall, Mark Denning, Xuegong Lei, Judy Y.-C. Chen, Yongjun Li, Yasujiro Murata, Nicholas J. Turro, and Malcolm H. Levitt (2013), ChemPhysChem, 10.1002/cphc.201300269.

  2. M. Z. Xu, F. Sebastianelli, B. R. Gibbons, Z. Bacic, R. Lawler et al. (2009) J. Chem. Phys.130, 224306.