Events
Statistics Seminar - Martingale optimal transport and applications to finance
Location: MB0.07
by Professor David Hobson, (University of Warwick)
Abstract: The optimal transport problem is about how to move n-interchangeable objects from one set of locations to another with minimum effort. Put more mathematically, we have mass distributed according to the law 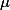 which we want to transport to the distribution
which we want to transport to the distribution  , and we want to do so in a way which minimises the total cost. In martingale optimal transport we add a further constraint that under the redistribution or transport, any mass at
, and we want to do so in a way which minimises the total cost. In martingale optimal transport we add a further constraint that under the redistribution or transport, any mass at  , on average stays at
, on average stays at  . In this talk I'll try to explain why MOT arises very naturally in mathematical finance, and talk about some simple and not-so-simple explicit solutions to some canonical problems.
. In this talk I'll try to explain why MOT arises very naturally in mathematical finance, and talk about some simple and not-so-simple explicit solutions to some canonical problems.
