For air at the scale of MEMS (Micro-ElectroMechanical Systems), the assumption of a continuum fluid is a comfortable one (for usual aeronautical altitudes, at least). However, what cannot be so safely assumed is a state of thermodynamicquasi-equilibrium in the gas. This assumption underpins conventional CFD (computational fluid dynamics) methods; it permits the use of non-slip boundary conditions and a linear relationship between stress and the rate of strain (Newtonian fluid behaviour). This leads to an important question: can the thermodynamic quasi-equilibrium assumption be justified at the micro-scale? An indication of the validity of the quasi-equilibrium assumption is given by the Knudsen number, Kn:

It has been estimated empirically that above a value of Kn≈10^-3, the quasi-equilibrium assumption breaks down and so-called non-equilibrium effects begin tobecome influential. For micro-devices this Kn limit is often exceeded, invalidating conventional methods of fluid analysis.

At Warwick, and in collaboration with Strathclyde University and Daresbury Laboratory, Warrington, we are developing efficient, but accurate, continuum models that can predict the most important non-equilibrium behaviour in MEMS. These tools have shown to predict many unusual phenomena, including thermal-stress slip flow. Thermal-stress slip flow is a curious rarefaction effect originally predicted by Sone in 1972. Using a solution of the Boltzmann equation (the fundamental kinetic equation), Sone showed that a steady-state flow circulation is generated between two stationary non-coaxial cylinders when there is a difference in their respective surface temperatures (Figure 1a, below). This cannot be predicted by conventional CFD, but Warwick’s code clearly captures this effect (Figure 1b).

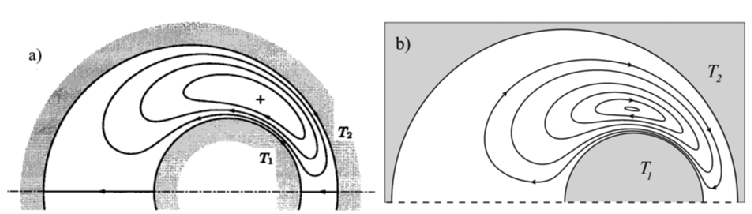
Figure 1. Streamlines of thermal-stress slip flow between non-coaxial cylinders (uniform temperatures T2>T1): (a) solution of the Boltzmann equation reproduced from Sone 1972, (b) solution from Warwick’s code.

Publications: