Mathematical problems for self assessment
Sample Problems
LAPLACE TRANSFORMS
1. Show from first principles (by using integration by parts) that the Laplace transform of 
is given by 
.
2. Find (from tables) the Laplace transforms of the following functions:
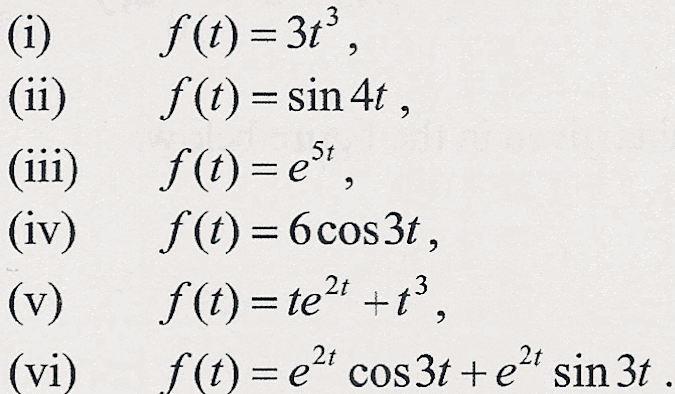
[Ans.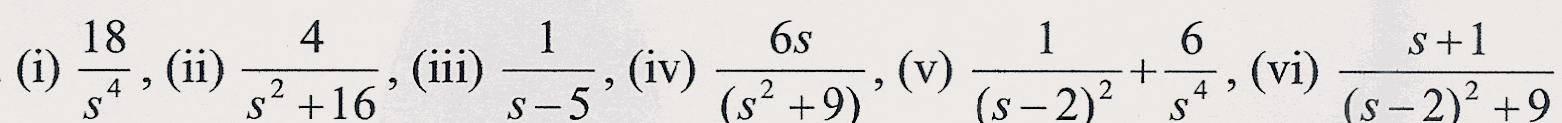
].
3. Find (from tables) the inverse Laplace transforms of the following functions:
(i) 
,
(ii) 
,
(iii) 
,
(iv) 
,
(v) 
,
(vi) 
.
[Ans. (i) 
, (ii) 
, (iii) 
, (iv) 
, (v) 
, (vi) 
].
4. Find the Laplace transforms of the following expressions:
(i)
;
,
(ii)
;
,
(iii)
;
[Ans. (i) 
, (ii) 
, (iii) 
, where 
is the Laplace transform of 
].
5. Solve the following differential equation using Laplace transforms
,
.
[Ans. 
].
6. Solve the following differential equation using Laplace transforms
,
.
[Ans. 
].
7. Solve the following differential equation using Laplace transforms
,
.
[Ans. 
].
8. Solve the following differential equation using Laplace transforms
,
.
[Ans. 
].
9. Solve the following differential equation using Laplace transforms
,
,
for some constant 
.
[Ans. 
].