Model Coupling and Applications

Authors: Oliver Dunbar, Yulong Lu, Luke Williams

Supervisors: Christoph Ortner, Andreas Dedner

Introduction

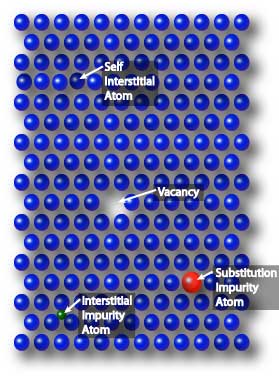
Material science, investigating the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties, has driven the development of modern science and technology. The most important features of the microstructure of an engineering material are the crystalline defects that are manipulated to control its behavior. The following picture demonstrates different defects in crystal.

The primary step to simulation of crystal defects is to model the physical process in mathematics. It is impossible, however, to use only atomistic models to simulate all material properties because of the sheer number of atoms that would be required for such a simulation. Fortunately, since defects occupy only a small proportion of bulk crystals, it is more advisable to model the elastic field using more efficient continuum models wherever they are reasonable to apply. This project is devoted to propose an optimized coupling mechanism between not only atomistic and continuum, but rather between the (now distinct) atomistic and nonlinear continumm, or atomistic and linear elastic continuum for point crystal defects.

Atomistic Model

In physical language, the atomistic problem objects to find the atomistic configuration that minimise the total energy of the physical system. In mathematics, with a reference deformation $u_0$ on lattice $\Lambda$ , if we define the atomistic energy difference functional

$\mathcal{E}^a(u) = \sum_{\ell \in \Lambda} (\Phi_\ell (u + u_0) - \Phi_\ell (u_0))$

then the atomistic problem is formulated as the following variational problem: find

$u^a \in \arg \min \mathcal{E}^a(u)$ .

However, due to the large number of atoms, it is unrealistic to perform defects simulation with the atomistic model.

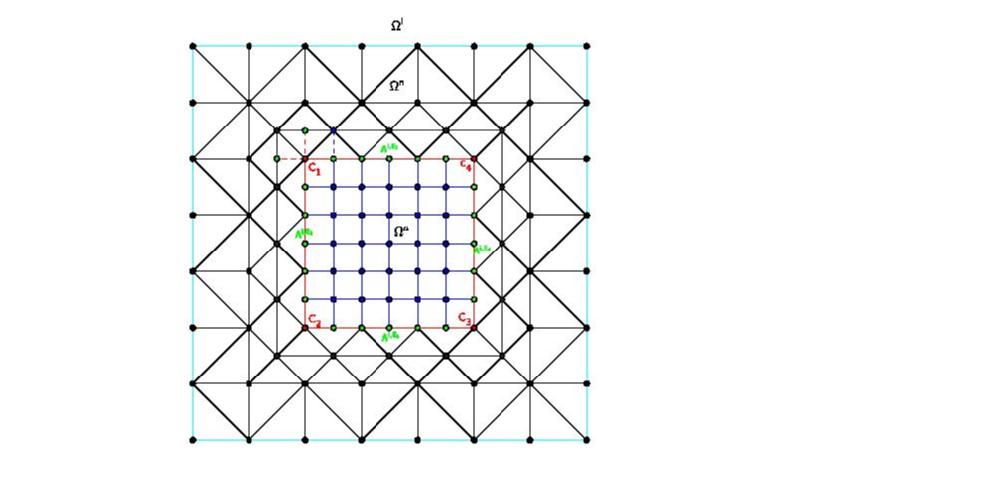
Atomistic / Nonlinear Elasticity Coupling Model

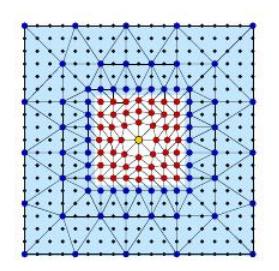
Since the defects only occupy a small part of the lattice, the deformation is relatively 'smooth' outside the defect region, where we can approximate the atomistic potential in terms of nonlinear elasticity theory. Assume that the computational domain is decomposed as $\Omega = \Omega^a \cup \Omega^n, \Lambda^{a,i} = \Lambda\cap \Omega = \Lambda^a \cup \Lambda^i$ , and that $\mathcal{T}_h$ is a regular mesh of $\Omega$ and $I_h$ is the associated linear interpolation operator.

We approximate the atomistic energy by the following nonlinear elasticity energy

$\mathcal{E}^{n}(u) := \int_{\Omega^c\cap\mathcal{T}_h} \big(W(\nabla (I_hy)) - W(\nabla (I_hu_0))\big) \text{d}x$

where $y = u + u_0$ and $W$ is the Cauchy-Born strain energy function

$W(F) := |\text{vol}(\ell)|^{-1}\Phi_\ell(F\cdot \mathcal{R}(\ell))$

In order to couple the atomistic and continuum model in a consistent way, we aslo need to modify the potentials and iteractions on the interface. Here, we take a simple Geometric Reconstruction Atomistic Continuum (GRAC) method to achive the ghost force free coupling. In particular, we define GRAC energy

$\mathcal{E}^{\text{GRAC}}(u) = \sum_{\ell \in \Lambda^i} w^i_l (\Phi^i_\ell(y) -\Phi^i_\ell(u_0))$

and the A/N coupling energy

$\mathcal{E}^{an}(u) := \mathcal{E}^{a}(u) + \mathcal{E}^{\text{GRAC}}(u) + \mathcal{E}^{n}(u)$

then the A/N coupling problem seeks to find

$u^{an} \in \arg \min \mathcal{E}^{an}(u)$

Atomistic / Nonlinear / Linear Elasticity Coupling Model

The nonlinear elasticity model can be further approximated by its linearisation wherever the deformation is small. In this case, the whole space $\mathbb{R}^2 = \Omega^a \cup \Omega^n \cup \Omega^l$ , the Cauchy Born energy function in $\Omega^l$ is linearised as follows

$W(\nabla (u + u_0)) \approx \underbrace{W(\nabla u_0)}_{= 0} + \underbrace{\partial W (\nabla u_0)}_{= 0}\cdot\nabla u + \frac{1}{2} \nabla u\cdot\underbrace{\partial^2 W (\nabla u_0)}_{\mu I}\nabla u$

anl

If we define the linearisation energy

$\mathcal{E}^l(u) := \frac{\mu}{2} \int_{\Omega^l}|\nabla u|^2$

and also the A/N/L energy functional

$\mathcal{E}^{anl}(u) := \mathcal{E}^{a}(u) + \mathcal{E}^{\text{GRAC}}(u) + \mathcal{E}^{n}(u) + \mathcal{E}^{l}(u)$

then the A/N/L coupling problem seeks to find

$u^{anl} \in \arg \min \mathcal{E}^{anl}(u)$

Atomistic/Linear Elasticity Coupling Model

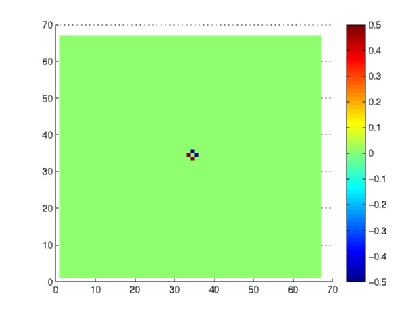
Example Simulation

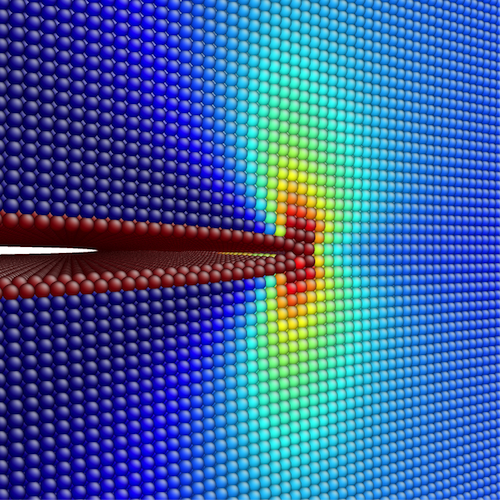
We run a simulation of the Atomistic-Nonlinear Elasticity model to demonstrate the method of the steepest descent model. The setup defect is given on the first image. The animation contains 2 figures. The left figure shows the simulated defect and right shows the modification proposed for the next step to update the system on the left (although this simulation samples 1:10). We exit the simulation when the gradient $\nabla \mathcal{E}^\text{model}(u) < 10^{-6}$

Acknowledgements

We acknowledge and thank the help of our supervisors Dr Christoph Ortner and Dr Andreas Dedner. We would also like to acknowledge the funding body EPSRC and the support from MASDOC CDT.

Contact: O.Dunbar at warwick.ac.uk, Yulong.Lu at warwick.ac.uk, Luke.D.Williams at warwick.ac.uk

MASDOC LOGO EPSRC LOGO