Atomistic / Linear Elasticity Coupling Model
Coupling Methods
Assume that the whole space with interface
. It is obvious that
where
.
And minimising is equivalent to finding solution to the following exterior Laplacian problem
Since is defined in infinite domain, it is unrealistic to apply finite element method to solve the problem numerically, instead, one can use boundary integral method to solve it. Furthermore, the solution
has the following integral representation in
with being the fundamental solution of Laplace equation in two dimensions. Using the Dirichlet boundary condition, we obtain
where
The integral equation has a unique solution in .
We will apply Galerkin boundary element method to discretize the integral equation. To that end, assume that is piece-wise constant function space on
and we define
then we find solution such that
. And we obtain the approximate solution as follows
We can transfer the boundary element discretisation error to the following consistency error of the linearisation energy
where denotes the radius of atomistic region. Recalling the consistency error for the GRAC energy in A/N/L coupling method is of
, we obtain the consistency error for A/L coupling method
Under the assumption of stability, we obtain the following error estimate
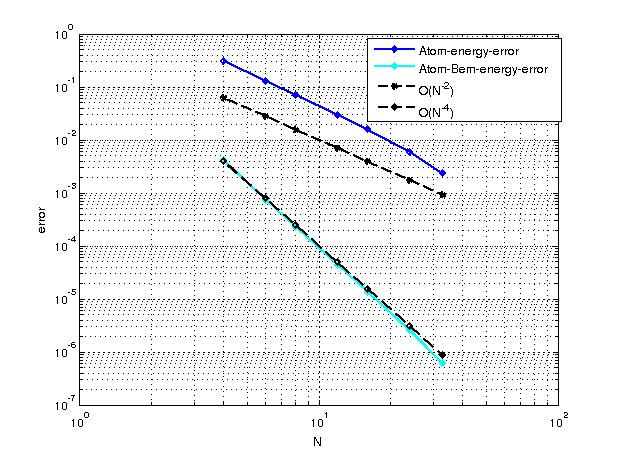
Numerical Results
The following figure shows the convergence rate for the error between atomistic energy and A/L energy, but the computational rate is which seems contradicting with the theoretical rate. However, we are not clear whether the constant in the error estimate depends on
, so the theoretical rate might be
in that case.
If we instead use the linearised Cauchy Born rule coupled to the atomistic region, and a FEM discretisation rather than a BEM one, we have the following results:
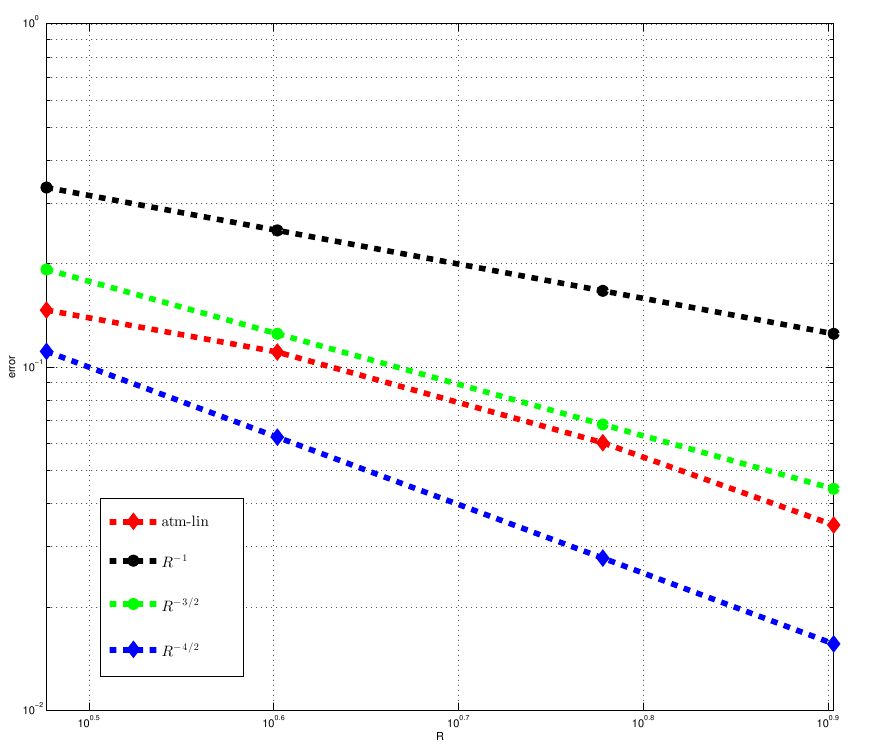
As with the other tests we scaled the atomistic region using the power for practical reasons, and it is promising we again observe a higher rate than this.