Multiserver Queues: Are two moments enough?

Authors: Matthew Dickson, Ifan Johnston, Jesse Pritchard, David Woodford.

Supervisors: Sayan Banerjee, Wilfrid S. Kendall

Introduction

Queues have become common place both in physical form made up of people and within networking and communications systems. In most cases these queues are of a first-come-first-served nature and often have multiple servers. For people who are designing these queueing systems it is useful to have an understanding of the distribution of the waiting time and in particular to know what the expected waiting time will be so decisions can be made, for example, on whether extra resourcing of the queue is needed.

Deterministic arrivals

$D(d)/M/K$ has deterministic inter-arrival times $d$ and Markovian job-size. By the time mesh we will mean the times $\mathcal{T}(d) := \{t_n = dn | n\in \mathbb{N}_0\}$ at which jobs from this queue arrive.
$Ge(d, p)/M/K$ has Geometric inter-arrival times (disallowing zero inter-arrival) with parameter $p$ over a mesh of size $d$ . That is, at each time $t\in \mathcal{T}(d)$ a job arrives with probability $p$ independently (and jobs arrive at no other times). Job sizes are exponentially distributied with mean $1$ .
$D(d)/D/K$ has deterministic arrivals on the mesh $\mathcal{T}(d)$ and jobs with constant size $1$ .
$M(\lambda)/M/K$ has exponentially distributed inter-arrival times with parameter $\lambda$ and exponentially distributed job-sizes with parameter $1$ .
We will denote by $\rho$ the traffic intensity given by $\rho = \frac{\lambda}{\mu K}$ , where $\lambda^{-1}$ is the mean inter-arrival time, and $\mu^{-1}$ is the mean job-size.

In [1] , they look at the set of waiting times with different job-size distributions (but with fixed first two moments) and investigate the size of this set. That is, they aimed to get upper (and lower) bounds on the infimum (resp. supremum) of these sets.

$W^{C^2}_h := \sup_G\{ \mathbb{E}[W^{M/G/K}] | \mathbb{E}[X] = 1, \mathbb{E}[X^2]=C^2 + 1, \text{where } X \sim G\}$

$W^{C^2}_l := \inf_G\{ \mathbb{E}[W^{M/G/K}] | \mathbb{E}[X] = 1, \mathbb{E}[X^2]=C^2 + 1, \text{where } X \sim G\}$

The bounds that they found are stated in the following theorems

Theorem:

For $0 < \rho < \frac{K-1}{K}$ and any finite $C^2 > 0$
$W^{C^2}_h \geq (C^2 + 1)\mathbb E [W^{M/D/K}]$
$W^{C^2}_l \leq \mathbb{E} [W^{M/D/K}]$

Theorem:

For $\frac{K-1}{K} \leq \rho < 1$ and any finite $C^2 > 0$
$W^{C^2}_h \geq \frac{(C^2 + 1)}{2}\mathbb E [W^{M/M/K}]$
$W^{C^2}_l \leq \mathbb{E} [W^{M/M/K}] + \frac{1}{1-\rho}\left[\rho - \frac{K-1}{K}\right]\frac{C^2 - 1}{2}$

The two cases $\rho < \frac{K-1}{K}$ and $\rho \geq \frac{K-1}{K}$ corrspond to light traffic and heavy traffic respectively.

More details can be found here

Asymptotics of M/M/K queues

As we have seen, the MMK queue has a central role in many of the discussions relating to more general queues, therefore it is useful to gain a better insight into its behaviour. We specifically look at the behaviour of $\mathbb E[W^{M/M/K}]$ as we increase the number of servers. In order to look at this behavour as $K\rightarrow \infty$ we hold the traffic intensity $\rho$ constant by increasing only the arrival rate of the customers.

It is known, see [2], that the stationary distribution of the M/M/K queue is given by

$\pi_i = \left\{ \begin{array}{lc} \pi_0 \frac{(K\rho)^i}{i!}& 0 \leq i < K\\ \pi_0 \frac{K^K\rho^i}{K!}& i \geq K \end{array} \right.$

where the normalisation $\pi_0$ is given by

$\pi_0 = \left(\sum_{j=0}^{K-1}\frac{(K\rho)^j}{j!} + \frac{(K\rho)^K}{K!}\frac{1}{1-\rho}\right)^{-1}$

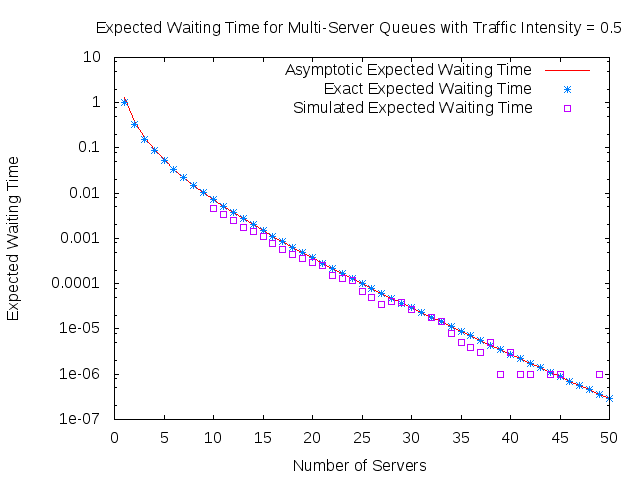
Tight bounds in the light traffic case

We have proven tight bounds on $\mathbb E[W^{M/M/K}]$ for $\rho \leq e^{-1}$ . This bound is given by

$\mathbb E[W^{M/M/K}] \sim \frac{1}{\sqrt{2\pi}} K^{-3/2}e^{K(1-\rho)}\frac{\rho^K}{(1-\rho)^2}$

for all fixed $\rho \in (0, e^{-1}]$ , as $K\rightarrow \infty$ . We also conjecture that this tight bound holds for all $\rho \in (0, 1)$ , but have not been able to prove this yet.

A graph that encourages this conjecture is seen below.

plotasymptotic

More details can be found here

References

[1] Gupta, Varun, et al. "On the inapproximability of M/G/K: why two moments of job size distribution are not enough." Queueing Systems 64.1 (2010): 5-48.

[2] Adan, Ivo, and Jacques Resing. "Queueing theory." (2002).

Acknowledgements

We acknowledge the funding body EPSRC and the support from MASDOC CDT.

MASDOC logo EPSRC logo