Discretised Euler-Lagrange equations

The Morley element

Now that we have existence for our problem we would like to solve it numerically. For this we use finite element method. We will be using a combination of Morley elements (for $u$ ) and piecewise affine elements (for $\phi$ ). The Morley elements are non-conforming ones, which means that the discretised function space is not a subspace of the original space. In fact, the solution of the discretised problem may not even be continuous. However, the advantage of this approach is that we can use lower order polynomial basis functions in each triangle, which makes the implementation of the numerical scheme much easier.

The Morley element is used widely throughout different elliptic PDE problems (see e.g. [1], [2], [4]). However, there are no results known to authors where a combination of Morley elements and piecewise affine elements is used in the same system.

We approximate $\Omega$ by a polyhedral domain $\Omega_h$ . For a subset $T\subset \Omega_h$ let $P^2 (T)$ denote the space of quadratic polynomials on $T$ . Let $\mathcal{T}$ be a triangulation of the computational domain $\Omega_h$ .
Definition: The Morley Element (see Figure 1) is the triple $(T, P^2 (T), \mathcal{N})$ where $T$ is a triangular element, $P^2(T)$ is the space of quadratic polynomials defined on $T$ , and $\mathcal{N}=\{\mathcal{N}_1,\mathcal{N}_2,\mathcal{N}_3,\mathcal{N}_4,\mathcal{N}_5,\mathcal{N}_6\}$ is the set of nodal variables, where

$\mathcal{N}_1(u_h)&:=&u_h(z_1),\qquad\mathcal{N}_4(u_h):=\frac{\partial{u_h}}{\partial\nu}u_h(z_4),$

$\mathcal{N}_2(u_h)&:=&u_h(z_2),\qquad\mathcal{N}_5(u_h):=\frac{\partial{u_h}}{\partial\nu}u_h(z_5),$
$\mathcal{N}_3(u_h)&:=&u_h(z_3),\qquad\mathcal{N}_6(u_h):=\frac{\partial{u_h}}{\partial\nu}u_h(z_6).$

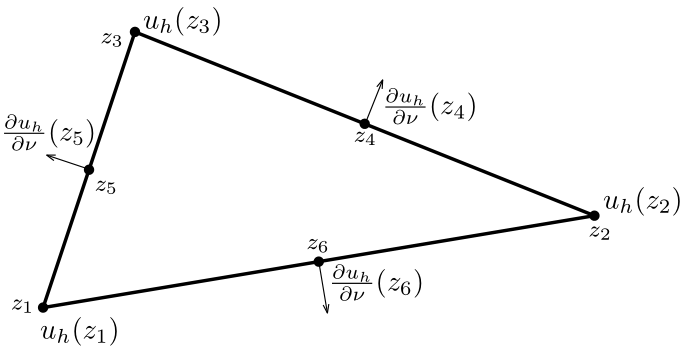
The Morley element

Figure 1: The Morley element

More details about the Morley element can be found in [3] and [1]. From here we can define the discretised function set:

$V_h&:=&\left\lbrace(u_h,\phi_h):\overline{\Omega_h}\to\mathbb{R}^2\,:\,\left.u\right|_T \in\mathcal{P}^2(T),\left.\phi\right|_T\in\mathcal{P}^1 (T)\,\,\,\forall{T}\in\mathcal{T},\right.$

$&&\phi_h \text{, } u_h \text{ agree on the vertices and } \frac{\partial u_h }{\partial \nu} \text{ agrees at the midpoints}$
$&& \left. \text{of the edges of any neighbouring triangles } T_i \text{ and } T_j \right\rbrace$

We note $V_h$ is the cartesian product of the Morley element space (for $u$ ) and the piecewise linear element space (for $\phi$ ).
Denote by $V_1,\ldots,V_N$ the nodes of the triangulation that are located on the boundary of $\Omega_h$ and let $M_1,\ldots,M_N$ denote the midpoints of the edges located at the boundary of $\partial\Omega_h$ .

Let

$\[ V_h^{f,g,p} := \left\lbrace (u,\phi )\in V_h$ $u(V_i) = g_i,$ $\phi (V_i ) = p_i,$ $\frac{\partial u}{\partial \nu_i} (M_i)= f_i ,$ $i=1,$ ...., $N \right\rbrace$

where $g_i = g(V_i)$ , $f_i = f(M_i)$ , $p_i = p(V_i)$ and $nu_i$ is the outward normal vector at $M_i$ , $i=1,\ldots , N$ .

The discretised Euler-Lagrange equations

Consider a symmetric, bilinear form $\widehat{a} (\cdot,\cdot): V_h \times V_h \to \mathbb{R}$ defined by

$\widehat{a} ((u,\phi ) , (v, \psi ) ) &:=& \sum_{T\in \mathcal{T}} \left( \kappa \int_T \Delta u \, \Delta v\, dx + \sigma \int_T \nabla u \cdot \nabla v \, dx + a \int_T \phi \, \psi \, dx + b \int_T \nabla \phi \cdot \nabla \psi \, dx \right.$

$\left. + c \int_T \phi \Delta v \, dx + c \int_T \psi \Delta u \,dx \right).$

The discretised Euler-Lagrange equations are:

Find $(u,\phi )\in V_h^{f,g,p}$ such that
$\widehat{a} ((u,\phi ) , (v, \psi ) ) =0$ $\forall (v,\psi )\in V_{h}^{0,0,0}$ .

This problem has a unique solution if $c\leq \sqrt{\kappa a}$ . We note that this is a weaker condition than $c < \sqrt{\kappa a } + \sqrt{\sigma b}$ , but we hope that this result could be improved. For the proof see Section 5.1.3 of the RSG report.

We do not prove convergence of the solution to the discretised problem to the exact solution. Some results regarding convergence of the Morley element method can be found in [4], [2], [5], [6] and [1], but the analysis of the convergence of the combination of Morley elements and piecewise affine elements exceeded the time-frame of the research study group. Instead we will present the numerical convergence results.

References

[1] M. Wang and J. Xu. The Morley element for fourth order elliptic equations in any dimensions. Numerische Mathematik, 2004.

[2] Shen, Q. A posteriori error estimates of the Morley element for the
fourth order elliptic eigenvalue problem

[3] Larson, M. G. and Bengzon, F. The Finite Element Method: Theory, Implementation and Applications

[4] Wang, L. H. Morley's element approximation to a fourth order variational
inequality with curvature obstacle

[5] Hu, J. and Shi, Z. and Xu, J. Convergence and optimality of the adaptive Morley element
method

[6] Li, M. and Guan, X. and Mao, S. New error estimates of the Morley element for the plate
bending problems