Stochastic Growth Models
Authors: Adam Bowditch, John Sylvester and Qiaochu Chen
Supervisors: Nikolaos Zygouras and Partha Dey.
We consider a long-range first-passage percolation model on the lattice
from 'Multiple phase transitions in long-range first passage percolation' under a specific class of distributions supported away from
as in 'Strict inequalities for the time constant in first passage percolation'. We have shown that in the critical and supercritical cases that the limiting shape of an appropriately scaled growth set is the unit
ball and in the subcritical case a limiting shape exists and that under some assumptions this deterministic shape has a flat piece which coincides with that of the nearest neighbour model.
This is a simulation of the growth set evolving over time in the supercritical regime.
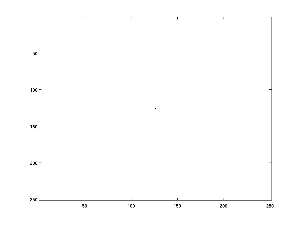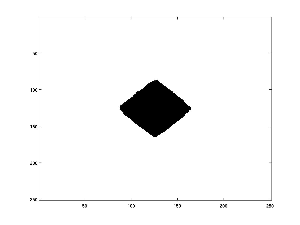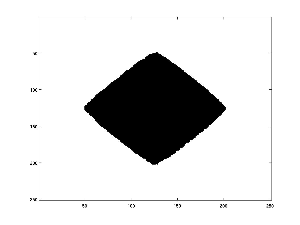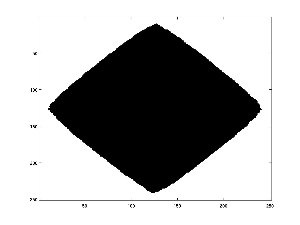
Let
be the edge set for the infinite complete graph on . To each
we assign an independent random weight
, where
are i.i.d. with common distribution
.
We fix then the random variable
represents the passage-time through the edge . For
, a finite
-path, we define the corresponding passage-time to be
Based on these , the first-passage time to reach
from
is defined to be the minimum passage-time over all finite
-paths from
to
:
where is the set of all finite
-paths from
to
. This defines a random metric on
which we refer to as the LRFPP metric. Using this first-passage time define the growth set
which is the ball of radius in this metric.
Cox & Durrett have shown, in their paper 'Some limit theorems for percolation with necessary and sufficient conditions', that in the nearest neighbour case where we use the edge set
that there exists a deterministic limiting shape such that for any
we have that
Marchand, in her paper 'Strict inequalities for the time constant in first passage percolation', (among others) have extended this result to characterise the existence of a flat piece on the boundary of . In particular letting
denote the critical threshold for oriented bond percolation in
and
the asymptotic growth speed of the oriented percolation, we can write
to be the line segment connecting
we have that
If then,
.
- If
then
.
- If
then
.
- If
then
.
We extend these results to the long-range model for three distinct cases depending on the value of .
References
- J.M. Hammersley, D.J.A. Welsh. First-passage percolation, subadditive processes, stochastic networks and generalized renewal theory. Proc. Internat. Res. Semin., Statist. Lab. Univ. California, Berkeley, Calif., pages 61 –110, 1965.
- J.T. Cox, R. Durrett. Some limit theorems for percolation with necessary and sufficient conditions. Ann. Appl. Probab., 9:583–603, 1981.
- Marchand, R. Strict inequalities for the time constant in first passage percolation. Ann. Appl. Probab., 12:1001–1038, 2002.
- S. Chatterjee, P. Dey. Multiple phase transitions in long-range first-passage percolation on square lattices. preprint. http://arxiv.org/abs/1309.5757.
Acknowledgements
We acknowledge and thank the help of our supervisors Dr Nikolaos Zygouras and Dr Partha Dey.
We also acknowledge the funding body EPSRC and the support from MASDOC CDT.


