LLT Polynomials

A useful object when dealing with domino tableau are the LLT Polynomials. They are symmetric functions and are defined as follows. For a skew shape $\lambda \setminus \gamma$ and parameter $q \in [0,1]$ , the corresponding LLT polynomial is:

$ G_{\lambda \setminus \gamma}(x, q^{\frac{1}{2}}) = \sum_{P:sh(P) = \lambda \setminus \gamma} q^{spin(P)} x^{weight(P)} $

If the content of P has $c_1$ 1s, $c_2$ 2s, ... , $c_n$ ns, then ${\textbf{x}}^{weight(P)} := \Pi_{i=1}^n x_i^{c_i}$ and we define spin(P) to be half the number of vertical dominoes in P

Calculating an LLT Polynomial

We wish to calculate the LLT polynomial associated with the shape [3,3], given variables $x=(x_1,x_2)$ . Because there are two variables, we look at all legal domino tableaux that have shape [3,3] that do not contain any numbers other than one or two. These can be seen below.

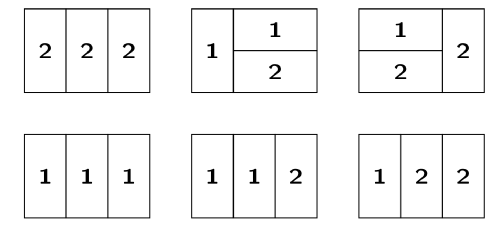
Considering the definition, and the diagram above, we can see that

$ G_{[3,3]}(x_1,x_2,q^{\frac{1}{2}})=q^{\frac{3}{2}}(x_1^3+x_1^2x_2^1+x_1^1x_2^2+x_2^3)+q^{\frac{1}{2}}(x_1^2x_2^1+x_1^1x_2^2) $