Tableaux

Definition: Young Diagram

A Young diagram of size n is a sequence $\lambda_1 \geq \lambda_2 \geq \cdots$ of non- negative integers such that $\sum_i \lambda_i = n$ . We denote this by $\lambda$ and draw it as a collection of unit boxes where each $\lambda_i$ is the length of a row.

The length $l(\lambda)=sup\{k \geq 1 | \lambda_k >0\}$ is the number of rows in $\lambda$ . We denote the set of all Young diagrams by $\mathbb{Y}$ , including the empty diagram $\emptyset=(0,0, \ldots)$ .

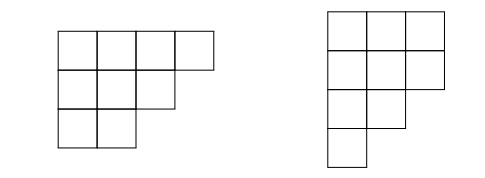
Below we see the Young diagram [4,3,2] on the left with its transpose on the right.

Definition: Young Tableau

A semi-standard Young tableau of shape $\lambda$ and rank N is a filling of boxes of a Young diagram $\lambda$ with numbers from 1 to N such that the numbers strictly increase along the columns and weakly increase along the rows.

Definition: Domino Diagram

A domino diagram is a Young diagram that can be tiled by combinations of 2x1 and 1x2 rectangles (which we call dominoes)

Definition: Domino Tableau

A domino tableau with shape $\lambda$ and rank $N$ is a filling of dominoes of a tiling of a domino diagram $\lambda$ with numbers from 1 to N such that the numbers strictly increase along the columns and weakly increase along the rows.

Definition: Schur Polynomial

For a given Young Diagram $\lambda$ , we defined the corresponding Schur polynomial by
$</p> <p>s_{\lambda}(X) = \sum_{P: sh(P)=\lambda} {\textbf{X}}^{weight(P)},</p> <p>$
If the content of P has $c_1$ 1s, $c_2$ 2s, ... , $c_n$ ns, then ${\textbf{x}}^{weight(P)} := \Pi_{i=1}^n x_i^{c_i}$ .